2.8. Определение дисперсии методом моментов

Преобразованием приведенных выше логических формул определе­ния дисперсии могут быть получены ее новые формулы для расчета, например, методом моментов, которым иногда значение дисперсии по­лучается быстрее.

===

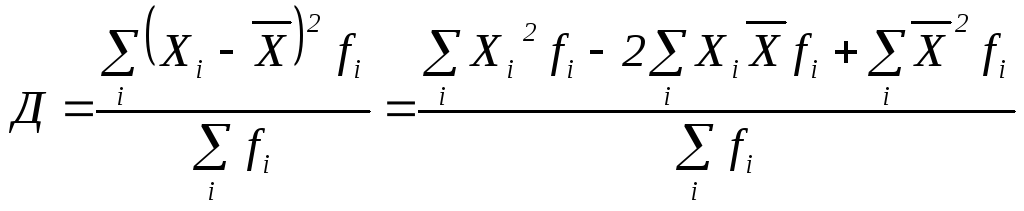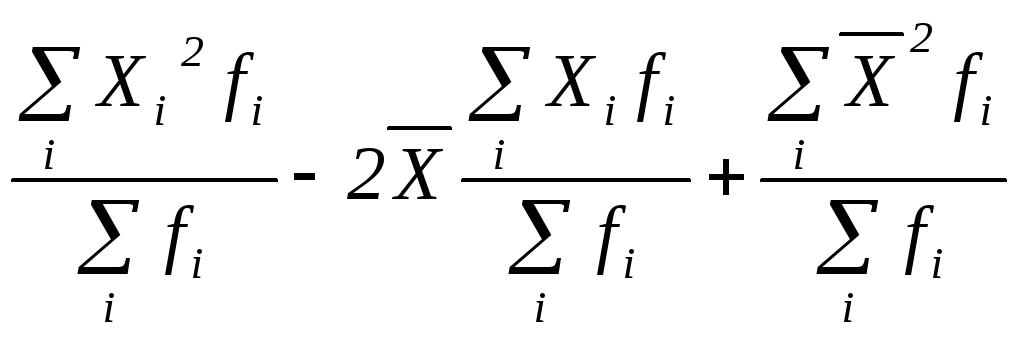Окончательно записываем, что дисперсия методом моментов определяется по формуле

Д = ,(1.32)

где – средняя квадратов статистических величин; – квадрат их средней величины.

Эти параметры нередко имеют и другие названия. Вычитаемое назы­вают начальным моментом первого порядка, уменьшаемое – начальным моментом второго порядка, а сама дисперсия при этом называется цен­тральным моментом второго порядка.

Для иллюстрации пользования формулами дисперсии рассмотрим простейший пример, приняв абстрактно Х₁ = 2, Х₂ = 4, Х₃ = 6, для которых среднее значение, очевидно, равняется = 4. Тогда дисперсия простая по логической формуле (1.24) будет равна

Д₃ = ((2-4)² + (4-4)² + (6-4)²)/3 = 8/3 = 2,67

Применив формулу моментов (1.32), получим тот же результат

Д₃ =(2² + 4² + 6 ² )/3 – 4² = 56/3 – 16 = 2,67

В данном примере быстрота определения дисперсии методом мо­ментов не достаточно ощутима, но она проявляется очень заметно при большом количестве статистических данных.

2.9. Свойства средней арифметической и дисперсии

В статистических расчетах эти характеристики статистической сово­купности зачастую применяются во взаимодействии. При этом с целью приведения их к удобному для анализа виду при громоздких значениях статистических величин используют следующие свойства.

1. Если каждую статистическую величину изменить на одно число (прибавить или отнять), то средняя арифметическая изменится на это число, а дисперсия при этом не изменится.

2. Если каждую статистическую величину изменить в одинаковое число раз (умножить или разделить), то средняя арифметическая изме­нится во столько же раз, а дисперсия изменится в квадрат таких раз.

Доказать эти свойства можно путем математических преобразований соответствующих формул, но гораздо проще доказательство получается с помощью следующего численного примера.

Принимая предыдущие три статистические величины с их значения­ми 2, 4, и 6, сначала прибавим к каждой из них 5, а потом умножим ка­ждую из них на 5. Тогда получим измененные значения статистических величин, представленные матрицей

X₁=2; X₁’=2+5=7; X₁’’=2*5=10.

X₂=4; X₂’=4+5=9; X₂’’=4*5=10.

X₃=6; X₃’=6+5=11; X₃’’=6*5=30.

= 4; ’=9; ’’=20.

Д=2,67; Д’=2,67; Д’’=66,67.

В этой матрице значения средних арифметических очевидны, а пер­воначальное значение дисперсии было найдено в предыдущем примере. Расчет других ее значений приведен ниже по логической формуле (1.24)

Д’= ((7-9)² + (9-9)² + (11-9)²)/3 = 2,67

Д’’= ((10-20)² + (20-20)² + (30-20)²)/3 = 66,67

Отмечаем, что отношение 66,67/2,67 дает ровно 25 или 5². То есть при увеличении каждой статистической величины в 5 раз дисперсия увеличилась в 25 раз. Аналогичные численные доказательства можно выполнить и в случаях противоположного изменения статистических величин.

2.10. Методические указания по теме

Методику расчета средних величин и коэффициентов вариации рас­смотрим на примере группы студентов или слушателей из 21 чел. (N =21), каждый из которых имеет возраст X = 28, 36, 30, 22, 22, 40, 29, 27, 21, 23, 35, 30, 32, 33, 29, 37, 29, 39, 23, 22, 22 лет. Требуется определить средний возраст и установить его типичность или не типичность с помощью линейного и квадратического коэффициентов вариации.

Поскольку данные не упорядочены, то средний возраст определяем по формуле (1.13) как простую среднюю арифметическую величину

= (28+36+30+…+23+22+22)/21 = 29 лет.

Для применения формулы средней арифметической взвешенной выполним первичную (дискретную) группировку данных, расположив их в порядке увеличения возраста и определяя повторяемость, встречаемость или частоту одинакового возраста, как показано в табл. 1.1.

Таблица 1.1

Первичная или дискретная группировка данных

Xi	21	22	23	27	28	29	30	32	33	35	36	37	39	40
fi	1	4	2	1	1	3	2	1	1	1	1	1	1	1	21

Тогда по формуле (1.14) средний возраст будет равен

= (21*1+22*4+23*2+…+37*1+39*1+40*1)/21 = 29 (лет).

Хотя результат и оказался одинаковым, но первичная группировка дает более четкое представление о структуре статистической совокуп­ности. В данном примере это возрастная структура группы студентов. К тому же, она позволяет перейти к определению линейного коэффици­ента вариации.

Так, по формуле (1.23) среднее линейное отклонение взвешенное равно

Л = 4,857 лет

а линейный коэффициент вариации по формуле (1.28) равняется

= 4,857/29 = 0,168

Вывод: средний возраст 29 лет является типичным для рассмотрен­ной группы студентов, т.к. расчетный коэффициент вариации оказался меньше его критериального значения (0,168 0,333).

Дополнительно определяется коэффициент осцилляции, для чего предварительно по формуле (1.31) находим размах вариации

R = 40-21 = 19 (лет).

Значит, по формуле (1.30) коэффициент осцилляции равняется

Кос = 19/29 = 0,655.

Для нахождения квадратического коэффициента вариации выполним вторичную (интервальную) группировку данных, используя формулу Стерджесса для определения оптимального количества интервалов п. Эта формула имеет вид

n = 1 +3,322 lg N, (1.33)

позволяя затем находить необходимый размах интервала как отношение

X_и = R / n. (1.34)

Подставляя данные примера в эти формулы, находим количество ин­тервалов n =1+ 3,322 lg 21 = 1+3,322*1,322 = 5,4. Так как количество интервалов не может быть дробным, то его нужно округлить до ближайшего целого числа (по правилам округления). То есть нужно принять 5 интервалов.

По формуле (1.32) размах интервала будет равен 19/5 = 3,8, то есть 3,8 года. Интервальная группировка данных приведена в первом столбце табл. 1.2, которая содержит также алгоритм и промежуточные расчеты.

Таблица 1.2 Промежуточные расчеты по интервальной группировке данных

Xi , лет	fi	ХИ	XИfi	ХИ-	(ХИ-)2	(ХИ-)2 fi
до 24,8	7	22,9	160,3	-6,333	40,111	280,7778
24,8-28,6	2	26,7	53,4	-2,533	6,418	12,83556
28,6-32,4	6	30,5	183	1,267	1,604	9,626667
32,4-36,2	3	34,3	102,9	5,067	25,671	77,01333
36,2-40	3	38,1	114,3	8,867	78,618	235,8533
Итого	21	—	613,9	—	—	616,1067

В табл. 1.2 пер­вый и последний интервалы открытые, не имея нижней или верхней границы диапазона, а промежуточные интервалы закрытые, имея обе границы. Нахождение середин закрытых интервалов затруднений не вызывает, а с открытыми интервалами поступают следующим образом: к открытому интервалу применяют размах соседнего (смежного), но так как размах всех интервалов в нашем примере одинаков и равен 3,8 года, то и здесь затруднений не должно быть.

У первого интервала отсутствует нижняя граница и находят ее путем вычитания размаха смежного интервала из имеющейся верхней грани­цы, получая тем самым закрытый интервал, середина которого опреде­ляется легко. В данном примере имеем 24,8–3,8 = 21 год, значит, середина этого интервала будет равна (21+24,8)/2 = 22,9 года.

У последнего интервала отсутствует верхняя граница и находят ее путем прибавления размаха смежного интервала к имеющейся нижней границе, получая тем самым также закрытый интервал. В данном при­мере имеем 36,2+3,8 = 40 (лет), значит, середина интервала 36,2-40 будет 38,1 лет.

По итогам табл. 1.2 определяются такие характеристики, как средний возраст по формуле (1.14)

= 613,9/21 = 29,2333 (лет).

Как видим, результат несколько отличается от предыдущего, что вы­звано неизбежным округлением расчетного количества интервалов. Чем больше количество интервалов и меньше их размах, тем меньше будет разница в результатах.

Затем по формуле (1.25) определяется взвешенная дисперсия откло­нений

Д = 616,1067/21=29,3384 лет².

Далее по формуле (1.26) находится среднее квадратическое отклоне­ние

= = 5,4165 лет.

И, наконец, по формуле (1.29) рассчитывается квадратический ко­эффициент вариации

= 5,4165 /29,2333 = 0,185.

По значению этого коэффициента делается вывод о типичности среднего возраста 29,23 лет для рассмотренной группы студентов, т.к. расчетное значение коэффициента вариации не превышает критериаль­ного (0,185 < 0,333).

Рассмотренный пример подтвердил возможность одинаковых выво­дов о типичности или не типичности средней величины с помощью ли­нейного и квадратического коэффициентов вариации и показал, что приход к конкретному выводу осуществляется значительно проще и быстрее с помощью линейного коэффициента.