3.4. Определение численности выборки

Разрабатывая программу выборочного наблюдения, иногда задаются конкретным значением предельной ошибки с уровнем вероятности. Не­известной остается минимальная численность выборки, обеспечиваю­щая заданную точность. Ее можно получить из формул средней и пре­дельной ошибок в зависимости от типа выборки. Так, подставляя фор­мулы сначала (1.35) и затем (1.36) в формулу (1.38) и решая ее относи­тельно численности выборки, получим следующие формулы

для повторной выборки n= ; (1.41)

для бесповторной выборки n= 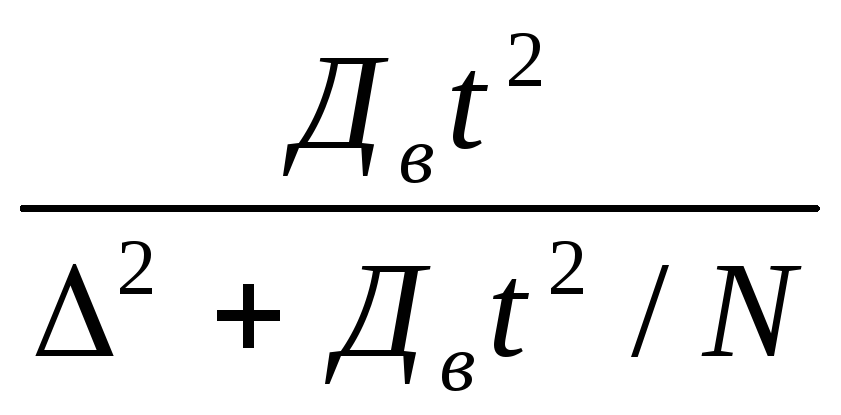. (1.42)

Кроме того, при статистических величинах с количественными при­знаками надо знать и выборочную дисперсию, но к началу расчетов и она не известна. Поэтому она принимается приближенно одним из сле­дующих способов:

• берется из предыдущих выборочных наблюдений;

• по правилу, согласно которому в размахе вариации укладывается примерно шесть стандартных отклонений (R/=6 или R/ 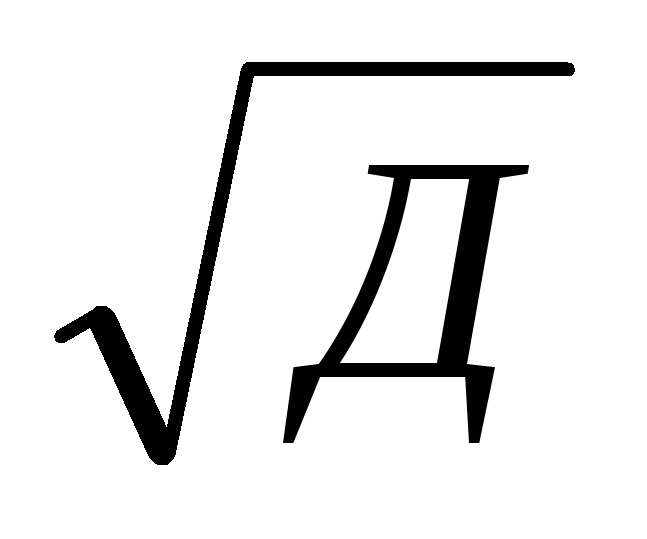= 6; отсюда Д = R² /36);

— по правилу «трех сигм», согласно которому в средней величине укладывается примерно три стандартных отклонения (/=3; отсюда=/3 илиД =²/9).

При изучении не численных признаков, если даже нет приблизи­тельных сведений о выборочной доле, принимается w = 0,5, что по фор­муле (1.37) соответствует выборочной дисперсии в размере Дв = 0,5(1-0,5) = 0,25.

3.5. Методические указания по теме

Методику расчетов при выборочном наблюдении рассмотрим на примере 10 %-й бесповторной выборки производственных фирм района с целью определения с вероятностью 0,954 средней стоимости их то­варной продукции. В табл. 1.3. приведены выборочные данные и про­межуточные расчеты.

Таблица 1.3

Выборочные данные о товарной продукции фирм и промежуточные расчеты

Xi, млн. руб.	fi, фирм	Xи	Xиfi	Хи-	(Хи -)2	(Хи -)2 fi
до 3	5	2	10	-14,9	222,01	1110,05
3-5	15	4	60	-12,9	166,41	2496,15
5-10	24	7,5	180	-9,4	88,36	2120,64
10-30	40	20	800	3,1	9,61	384,4
30 и более	16	40	640	23,1	533,6	8537,76
Итого	100	—	1690	—	—	14649,02

В этой таблице первые два столбца представляют собой результаты интервальной группировки выборочных данных, а в остальных столб­цах на ее основе выполнены необходимые расчеты, аналогично преды­дущим методическим указаниям.

Так, по формуле (1.14) определена средняя выборочная стоимость товарной продукции

= 1690 /100 = 16,9 млн. руб.

Затем по формуле (1.25) определяется выборочная дисперсия

Д_в= 14649 /100 = 146,49 млн. руб² .

Теперь по формуле (1.36) можно вычислить среднюю ошибку бесповторной выборки

== 1,148 (млн.руб).

При этом общее число фирм N = 1000, т.к. по условию выбранные 100 фирм составляет 10% от общего числа (элементарная задачка на проценты).

Наконец, по формуле (1.38) находим предельную ошибку выборки, учитывая, что при заданной вероятности 0,954 коэффициент доверия равен 2. То есть = 2*1,148 = 2,3 млн. руб.

Следовательно, средняя стоимость товарной продукции всех фирм района с вероятностью 0,954 находится в доверительном интервале

(16,9-2,3) (16,9+2,3) или 14,6 млн. руб. 19,2 млн. руб.

Далее рассмотрим методику расчета доверительного интервала по альтернативному признаку, поставив цель определения в районе доли фирм с товарной продукцией до 10 млн. руб.

Из табл. 1.3 находим, что выборочная доля таких фирм составляет

w = (5+15+24)/100 = 0,44.

Выборочная дисперсия по формуле (1.37) равняется

Дв = 0,44(1 -0,44) = 0,246.

Тогда средняя ошибка бесповторной выборки по формуле (1.36) составит

== 0,047.

Наконец, предельная ошибка по формуле (1.38) с учетом того, что при вероятности 0,954 коэффициент доверия 2, будет равна = 2*0,047= 0,094.

Значит, в районе доля фирм с товарной продукцией до 10 млн. руб. при вероятности 0,954 находится в доверительном интервале

(0,44-0,094) р (0,44+0,094) или 0,346 р 0,534 или 34,6% р 53,4%.

Отметим, что в случае представления выборочных данных в дис­кретном виде отпадает необходимость нахождения середин интервалов, что исключает третий столбец табл. 1.3. В остальных столбцах следует вместо Xи использовать X_i.