5.7. Индексы фиксированного (постоянного) и переменного состава

В полученной трехфакторной модели (1.87) второй и третий индексы запишем подробно по формулам их определения, а третий еще и сократим на . Тогда сначала будем иметь

I_Q =====,

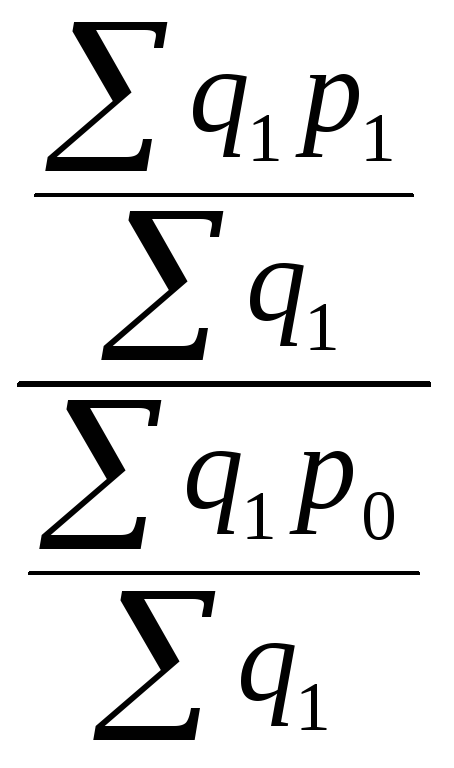а, произведя очевидное сокращение и обозначив

=- индекс переменного состава,(1.98)

получим общий индекс выручки в виде формулы

I_Q =.(1.99)

=называется индексом фиксированного (постоянного) состава. (1.100)

Следовательно, общий индекс выручки есть произведение простого общего индекса количества товаров и индекса переменного состава. По­следний часто путают с ценовым индексом Пааше, хотя формулы их определения совершенно разные.

Из формулы (1.99) можно заключить, что индекс переменного соста­ва есть частное от деления общего индекса выручки на простой общий индекс количества товаров, тогда как ценовый индекс Пааше наравне с формулой (1.77) возможно определять как отношение общего индекса выручки и количественного индекса Ласпейреса.

Изложенные математические выкладки позволяют общий индекс выручки определять следующими семью способами

=======.

Результат расчета любым способом должен быть одинаковым и это яркий пример того, что истина всегда одна, хотя пути ее достижения могут быть разными.

5.8. Методические указания по теме

Процесс определения всевозможных индексов и факторного анализа сложного явления рассмотрим на примере двух фирм, выпускающих однородный продукт. Исходные данные приведены в табл. 1.6.

В табл. 1.6 итоговое количество продукта есть сумма его количества по фирмам, а итоговая цена представляет собой среднюю арифметиче­скую взвешенную величину, найденную по формуле (1.13).

Таблица 1.6 Результаты работы двух фирм по выпуску однородного продукта

Фирма	Базисный период (база)		Отчетный период (отчет)
	Количество продукта q0, тыс.ед.	Отпускная цена p0, руб/ед.	Количество продукта q1, тыс.ед.	Отпускная цена p1 , руб/ед.
1	100	20	140	15
2	150	22	160	25
Итого	250	21,20	300	20,23

Так, для базисного периода она равна

==(100*20+150*22)/(100+150) = 5300/250 = 21,20 руб./ед.

Для отчетного периода средняя цена равняется

==(14*15+160*25)/(140+160) = 6100/300 = 20,23 руб./ед.

После этого в табл. 1.7 ведется расчет индивидуальных индексов.

Таблица 1.7

Определение выручки и индивидуальных индексов

Выручка и ин­дексы	База по фирмам		Отчет по фирмам
	1	2	1	2
Выручка Q, тыс. руб.	100*20=2000	150*22=3300	140*15=2I00	160*25=4000
Изменение выруч­ки , тыс. руб.			2100-2000=100	4000-3300=700
Доля фирм в ко­личестве продукта d	100/250=0,4	150/250=0,6	140/300=0,467	160/300=0,533
Индивидуальные индексы:
количества iq			140/100=1,4	160/150=1,067
отпускных цен ip			15/20=0,75	25/22=1,136
доли фирм id			0,467/0,4=1,167	0,533/0,6=0,889
выручки iQ			2100/2000=1,05	4000/3300=1,212

Из табл.1.7 заключаем, что общая выручка по периодам составляет:

= 2000+3300 =5300 тыс. руб.

= 2100+4000 =6100 тыс. руб.

Ее абсолютное изменение равно =6100-5300=800 тыс. руб., а общий индекс изменения равняется = 6100/5300 = 1,151.

Контроль правильности расчетов по табл. 1.7. заключается в сле­дующем.

1. Общее изменение выручки должно равняться сумме ее частных изменений: = 100+700 = 800 тыс. руб.

2. Произведение факторных индивидуальных индексов по периодам должно равняться соответствующему индивидуальному индексу выруч­ки: i_Q1=1,4*0,75 =1,05; i_Q2= 1,067*1,136 = 1,212.

3. Сумма долей количества продукта по периодам должна равняться единице: 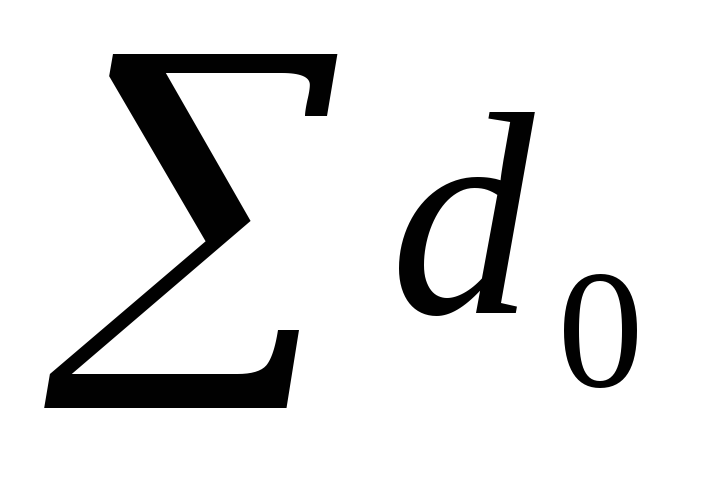=0,4+0,6 = 1;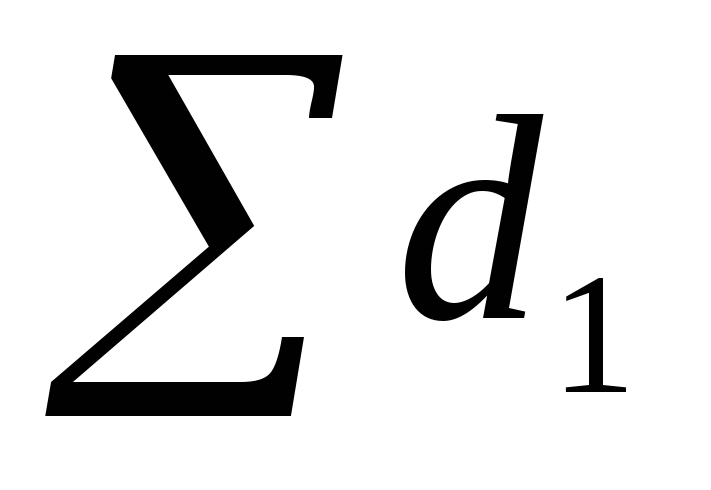=0,467+0,533=1.

Затем переходим к расчету простых и агрегатных общих индексов. Простой общий индекс количества продукта - по формуле (1.72)

=(140+160)/(100+150)=300/250=1,2.

Агрегатный общий количественный индекс Ласпейреса - по форму­ле (1.75)

==6320/5300=1,192.

Агрегатный общий ценовый индекс Пааше - по формуле (1.77)

==6100/6320=0,965.

Контроль по формуле I_Q = = 1,192*0,965 = 1,151.

Агрегатный общий ценовый индекс Ласпейреса - по формуле (1.76)

==5250/5300=0,9905.

Агрегатный общий количественный индекс Пааше — по формуле (1. 78)

=6100/5250=1,162.

Контроль по формуле I_Q = = 0,9905*1,162 =1,151.

Средняя геометри­ческая величина из индексов Ласпейреса и Пааше (по методике Фишера) по формулам (1.79) и (1.80)

==1,1769

==0,9777

Простая средняя арифметическая величина из индексов Ласпейреса и Пааше (по методике Воронина) по формулам (1.81) и (1.82)

= (1,192+1,162)/2 = 1,177

= (0,9905+0,965)/2 =0,9778

Общий индекс выручки как средний из ее индивидуальных индек­сов:

— с использованием только базисной выручки — по формуле (1.83)

I_Q==1,151.

— с использованием только отчетной выручки — по формуле (1.84)

I_Q==1,151.

Индекс структурных сдвигов — по формуле

===21,07/21,2=0,994.

Контроль по формуле == 1,2*0,994*0,965 = 1,151.

Индекс переменного состава — по формуле

===20,33/21,2=0,959.

Контроль по формуле == 1,2*0,959=1,151.

Далее выполняется факторный анализ общей выручки. Так ее изме­нение за счет изменения общего количества продукта определится по формуле (1.89)

= (1,2-1)*5300 = 1060 тыс. руб.

Изменение общей выручки за счет структурных сдвигов в количест­ве продукта находится по формуле (1.90)

= 1,2*(0,994-1)*5300 = -38 тыс. руб.

Изменение общей выручки за счет изменения отпускных цен - по формуле (1.91)

=1,2*0,994*(0,965-1)*5300 = -222 тыс. руб.

Контроль по формуле (1.92): = 1060-38-222 = 800 тыс. руб.

Результаты факторного анализа общей выручки заносятся в табл. 1.8.

Наконец, ведется факторный анализ изменения частной выручки по формулам (1.94)-(1.96). Так у первой фирмы изменение выручки за счет изменения общего количества продукта равно

=(1,2-1)*2000 = 400 тыс. руб.

Аналогично у второй фирмы = (1,2-1)*3300 = 660 тыс. руб.

Контроль: =400+660=1060 тыс.руб.

У первой фирмы изменение выручки за счет структурных сдвигов в количестве продукта равно

=1,2*(1,167-1)*2000 = 401 тыс. руб.

Аналогично у второй фирмы

=1,2*(0,889-1)*3300 = -439 тыс. руб.

Контроль: =401-439= -38 тыс.руб.

У первой фирмы изменение выручки за счет изменения отпускной цены равно

=1,2*1,167*(0,75-1)*2000 = -701 тыс. руб.

Аналогично у второй фирмы

=1,2*0,889*(1,136-1)*3300 = 479 тыс. руб.

Контроль: = -701+479= -222 тыс.руб.

Результаты факторного анализа частной выручки также заносятся в табл.1.8, в которой все числа оказались взаимно согласованными.

Таблица 1.8

Результаты факторного анализа сложного явления

Фирма	Изменение выручки, тыс.руб.	В том числе за счет изменения
		количества продукта	структурных сдвигов	отпускных цен
1	100	400	401	-701
2	700	660	-439	479
Итого	800	1060	-38	-222

Таблица 1.8 свидетельствует о правильности проведенного факторного анализа, поскольку в ней факторные изменения выручки, как по столбцам, так и по строкам в сумме равняются ее изменениям по отдельным факторам, фирмам и в целом.