3. Моменты распределения Показатели формы распределения

3.1. Моменты распределения

Для подробного описания особенностей распределения используют дополнительные характеристики – моменты распределения.

Момент распределения k-го порядка – средняя величина отклонений k-й степени от некоторой постоянной величины А:

. (3.1)

Практически используют моменты первых четырех порядков. Если А = , то моменты центральные;А = 0, то моменты начальные; А – произвольное число, то моменты условные.

Начальные моменты	Центральные моменты	Нормированные моменты
(3.2) m0 = 1; m1 – средняя арифметическая ()	(3.3) = 1; = 0 –средний квадрат отклонений, дисперсия (s2)	(3.4) μ0=1; μ1=0; μ2=1; –показатель асимметрии

3.2. Показатели формы распределения

Нормированный момент третьего порядка является показателем асимметрии распределения :

. (3.5)

Степень существенности асимметрии характеризуется средней квадратической ошибкой, которая зависит от объема наблюдения:

, (3.6)

Если , то асимметрия существенна.

При симметричном распределении варианты, равноудаленные от , имеют одинаковую частоту, поэтому = 0, а следовательно, и μ3=0.

Если μ3 < 0, то в вариационном ряду преобладают (имеют большую частоту) варианты, которые меньше , т.е. ряд отрицательно ассиметричен (или с левосторонней скошенностью – более длинная ветвь влево). Положительная асимметрия (правосторонняя скошенность – более длинная ветвь вправо) характеризуется значением μ₃ > 0 (рис. 2.1). В качестве показателя асимметрии применяется и коэффициент асимметрии Пирсона (As):

. (3.7)

Если As= 0, (т.е. ), то распределение симметричное (нормальное).

Если As < 0, то имеет место левосторонняя асимметрия.

Если As > 0,то имеет место правосторонняя асимметрия.

Если |As| > 0,25, то асимметрия значительна; если |As| < 0,25 – незначительна.

Рис. 2.1 Асимметрия распределения

Нормированный момент четвертого порядка характеризует крутизну (заостренность) графика распределения:

. (3.8)

Для нормального распределения μ₄ = 3, поэтому для оценки крутизны исследуемого распределения в сравнении с нормальным из μ₄ вычитается 3 и таким образом рассчитывается показатель эксцесса:

. (3.9)

Если Ex = 0, то распределение симметрично;

Ex > 0, то распределение островершинное;

Ex < 0, то распределение плосковершинное (рис. 3.2).

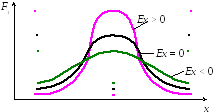
Рис. 3.2. Эксцесс распределения

3.3. Теоретические кривые распределения

Анализ вариационных рядов предполагает выявление закономерностей распределения, определение и построение (получение) некой теоретической (вероятностной) формы распределения. Характер распределения лучше всего проявляется при большом числе наблюдений и малых интервалах. В этом случае графическое отображение эмпирического вариационного ряда принимает вид плавной кривой, именуемой кривой распределения. Кривая распределения может рассматриваться как некая теоретическая (вероятностная) форма распределения, свойственная определенной совокупности в конкретных условиях.

Таким образом, анализируя частоты в эмпирическом распределении, можно описать его с помощью математической модели – закона распределения, установить по исходным данным параметры теоретической кривой и проверить правильность выдвинутой гипотезы и типе распределения данного ряда.

При исследовании закономерностей распределения очень важно выдвинуть верную гипотезу о типе кривой распределения, так как, если кривая описана математически (с помощью уравнения) верно, она более точно отражает закономерности данного распределения и может быть использована в различных практических расчетах и прогнозах. Кроме того, в этом случае можно сформулировать рекомендации для принятия практических решений.

Теоретическое распределение случайной величины – это математическое выражение функциональной зависимости значений случайной величины  x и вероятности ее попадания в соответствующий интервал.

Для построения функции теоретического распределения необходимо знать иs и обосновать вид кривой из сведений об экономическом явлении или процессе. Рассмотрим только нормальное распределение, поскольку именно оно наиболее широко применяется при построении статистических моделей.

Распределение непрерывной случайной величины x называют нормальным, если соответствующая ей плотность распределения выражается формулой

,

(3.10)

или ,

где x – значение изучаемого признака;

– средняя арифметическая ряда;

s² – дисперсия значений изучаемого признака;

s – среднее квадратическое отклонение изучаемого признака;

π = 3,1415926; е = 2,7182;

–нормированное отклонение.

Кривая нормального распределения (рис. 3.3) симметрична относительно вертикальной прямой , поэтому среднюю арифметическую ряда называютцентром распределения.

Случайные величины, распределенные по нормальному закону, различаются значениями параметров иs, поэтому важно выяснить, как эти параметры влияют на вид кривой нормального распределения.

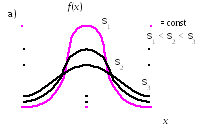
Если не меняется, а изменяется толькоs, то:

1. чем меньше s, тем более вытянута кривая (рис. 3.3, а), а так как площадь, ограниченная осью 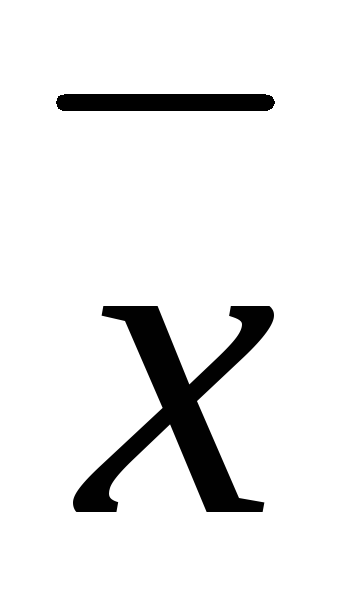и данной кривой, равна 1, то вытягивание вверх компенсируется сжатием около центра распределенияи более быстрым приближением кривой к оси абсцисс;

2. чем больше s, тем более плоской и растянутой вдоль оси абсцисс становится кривая.

Если s остается неизменной, а изменяется, то кривые нормального распределения имеют одинаковуюформу, но отличаются друг от друга положением максимальной ординаты (рис 3.3, б).

Особенности кривой нормального распределения.

1. Кривая симметрична и имеет максимум в точке, соответствующей значению .

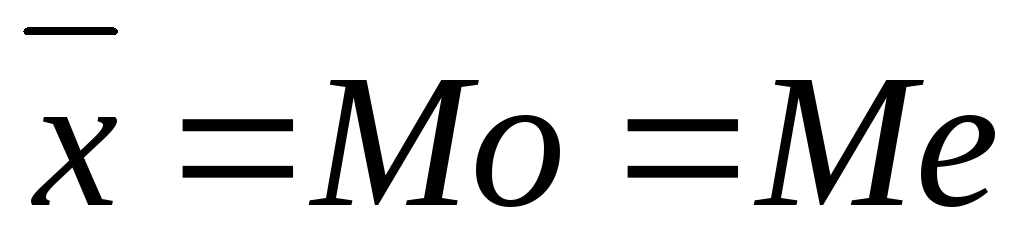2. Кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. Чем больше отдельные значения x отклоняются от 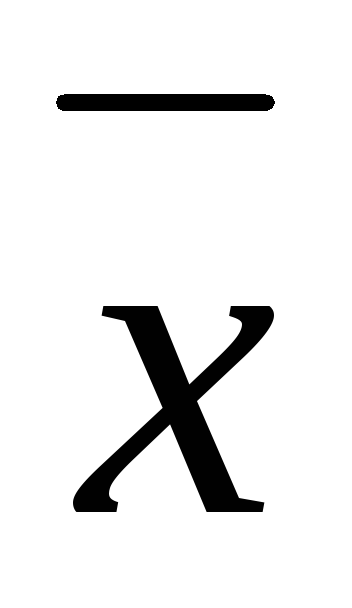, тем реже они встречаются.

3. Кривая имеет две точки перегиба на расстоянии ±s от .

4. Площадь между ординатами, проведенными на расстоянии 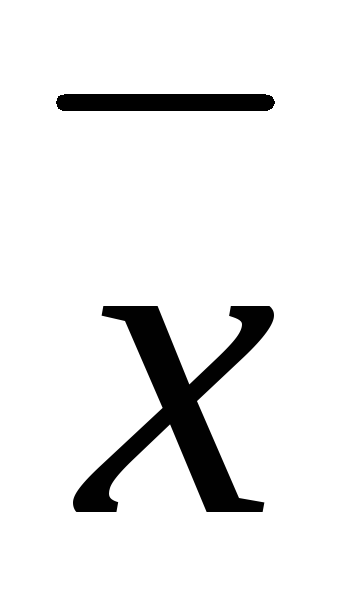±s (заштрихованная область на рис 3.3, б), составляет 0,683. Это означает, что 68,3% всех исследуемых единиц (частот) отклоняется от средней арифметической не более, чем на s, т.е. находится в пределах 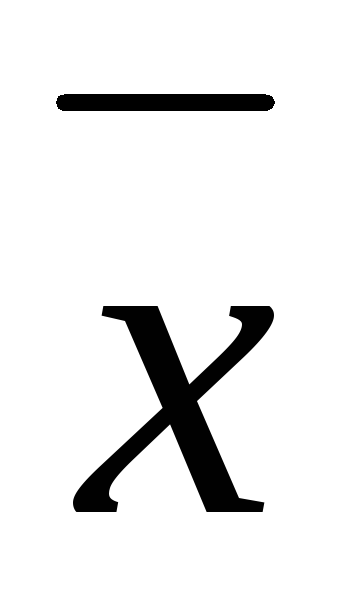±s. В промежутке ±2s находится 95,4%, а в промежутке ±3s соответственно, 99,7% всех единиц исследуемой совокупности.

5. Коэффициенты асимметрии и эксцесса равны нулю.

б)

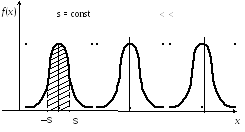
Рис. 3.3 Кривые нормального распределения