8.4.2. Выбор наилучшего тренда при прогнозировании

При выборе уравнения тренда можно руководствоваться средней ошибкой аппроксимации

, %. (6.26)

5÷7% – хорошая аппроксимация.

Доверительные интервалы прогноза определяются по дисперсии уточненного тренда

, %. (6.27)

где y_t – фактические уровни ряда;

– расчетные (трендовые) значения;

n – длина ряда;

m – число параметров в уравнении тренда (без свободного члена).

Доверительный интервал с учетом табличного значения критерия Стьюдента , равен

. (6.28)

Если распространить этот интервал на следующий отрезок времени, то надо ввести поправочный коэффициент q, зависящий от длины ряда и периода l упреждения

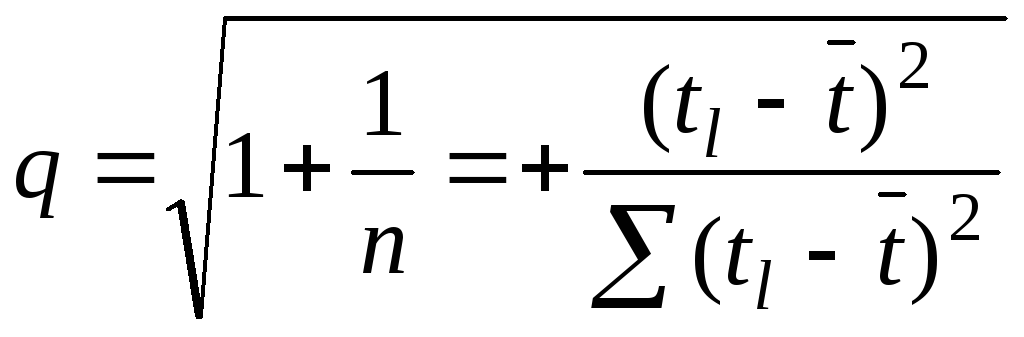, (6.29)

где n – длина ряда;

t_l – порядковый номер прогнозируемого периода (t_l = n + l);

– порядковый номер середины ряда.

Тогда ошибка прогноза

. (6.30)

. (6.31)

7. Экономические индексы

Индексом в статистике называется относительный показатель, характеризующий изменение величины какого-либо явления по сравнению с эталоном.

Таблица – Классификация индексов

Классификационный признак	Вид индексов
1. Содержание изучаемых объектов	Количественные (объемные) индексы (физического объема, товарооборота национального дохода)		Качественные индексы (интенсивности) (курса валют, цен, себестоимости, производительности труда)
2. Степень охвата элементов совокупности	Индивидуальные (изменение одного показателя однотоварного)		общие (групповые или субидексы (по отраслям))
3. Метод расчета	Агрегатные		Средние
4. База сравнения	Динамические		Территориальные (например, индекс цен на товары в РФ и ФРГ)
5. Вид весов	С постоянными весами		С переменными весами
6. Состав явления	Постоянного состава	Переменного состава		Структурных сдвигов
7. Период исчисления	Годовые	Квартальные		Помесячные и т.д.

Таблица – Обозначения индексируемых величин

Обозначение	Индексируемая величина		Обозначение	Индексируемая величина
q	количество (объем) какого-либо товара в натуральном выражении		t	затраты времени на производство единицы продукции, трудоемкость
p	цена единицы товара		W	выработка продукции в единицу времени или на одного работника (производительность труда)
pq	товарооборот (стоимость продукции)
z (c)	себестоимость единицы продукции		T=tq	общие затраты времени на производство продукции или численность работников
y	урожайность отдельных сельскохозяйственных культур
П	посевная площадь под отдельными культурами

7.1 Общие индексы количественных показателей

Индекс физического объема продукции показывает относительное изменение стоимости продукции из-за изменения объема производства.

Индивидуальный индекс: , (7.1)

Агрегатный индекс: , (7.2)

где q₁ и q₀ – объем выпуска продаж в базисном и отчетном периодах соответственно;

p₀ – цена в базисном периоде.

Индекс товарооборота (или стоимости продукции), показывает во сколько раз изменилась стоимость продукции.

Агрегатный индекс товарооборота

. (7.4)

На сколько изменилась стоимость продукции показывает разница между числителем и знаменателем индекса:

. (7.3)

При построении индекса физического объема продукции в качестве соизмерителей (весов) принимаются сопоставимые, неизменные, фиксированные цены, отличающиеся от текущих (действующих) цен (это в условиях инфляции могут быть цены предшествующего периода) или себестоимость продукции z₀. В этом случае индекс характеризует изменение издержек производства.

. (7.5)

Аналогично строятся индексы товарооборота и потребления.

Значение общего индекса I_pq зависит от изменения двух индексируемых величин объема продукции (q₀, q₁) и цен (p₁,p₀).

В зависимости от вида исходных данных можно исчислить средние взвешенные (арифметические) индексы физического объема.

Если неизвестно q₁, но дано значение q₀ и , а также стоимость продукции базисного периодаp₀, то средний арифметический индекс физического объема равен:

. (7.6)

Средний гармонический индекс физического объема используется для аналитических оценок в случае, когда неизвестно q₀, но дано значение q₁ и , а также стоимость продукции базисного периодаp₀:

. (7.7)

Индекс физического объема в прошлом вычисляется в сопоставимых, фиксированных ценах и отражает динамику выпуска продукции. В торговле чаще вычисляется в фактических ценах, отражая одновременное изменение цен и объема.

Пример Предприятие выпускает 3 вида неоднородной продукции. Данные об их производстве и ценах на них за два периода приведены в таблице (графы 1–5). Определить индивидуальные и агрегатные индексы физического объема.

Товар	Выработано тыс. единиц		Цена за единицу товара, руб.		Стоимость продукции в базисных ценах, тыс.руб.		Индивидуальный индекс физического объема
	базисный период	отчетный период	базисный период	отчетный период	базисный период	отчетный период
	q0	q1	p0	p1	q0p0	q1p0
А	80	60	13	16	1040	780	0,750
Б	50	30	18	20	900	540	0,600
В	40	35	6	8	240	210	0,875
Σ	—	—	—	—	2180	1530	—

Агрегатный индекс физического объема:

= 0,702 (70,2%).

Вычитая из числителя знаменатель = 1530 – 2180 = –650, определяем, что в абсолютном выражении за счет уменьшения выпуска стоимость продукции в отчетном периоде уменьшилась на 650 тыс.руб.