
- •Организация и функции статистических служб
- •Понятие о статистической информации
- •Статистическое наблюдение
- •Принципы построения статистических группировок
- •Вариационные ряды
- •Графическое отображение вариационных рядов
- •Пример 3.1.
- •Обобщающие статистические показатели
- •1. Средние величины
- •1.1 Средние степенные величины
- •1.2 Средние структурные величины
- •2. Анализ вариационных рядов
- •2.1. Показатели вариации
- •2.1.1. Свойства дисперсии
- •2.1.2 Вариация альтернативного признака
- •2.2. Виды дисперсий в совокупности, разделенной на части. Правило сложения дисперсий
- •3. Моменты распределения Показатели формы распределения
- •3.1. Моменты распределения
- •3.2. Показатели формы распределения
- •3.3. Теоретические кривые распределения
- •4. Выборочное наблюдение в статистике
- •4.1. Закон больших чисел и предельные теоремы
- •Выборочное наблюдение
- •4.2. Ошибка выборки для альтернативного признака
- •4.3 Определение необходимой численности выборки
- •4.4 Формы организации выборочного наблюдения
- •5. Статистические методы изучения взаимосвязи социально-экономических явлений
- •5.1 Регрессионный анализ
- •5.2 Корреляционный анализ
- •6. Ряды динамики
- •6.1 Анализ динамических рядов
- •6.2 Методы анализа тенденций рядов динамики
- •6.3 Сезонные колебания
- •6.4. Статистические методы прогнозирования экономических показателей
- •6.4.1. Прогнозирование на основе экстраполяции тренда
- •8.4.2. Выбор наилучшего тренда при прогнозировании
- •7. Экономические индексы
- •7.1 Общие индексы количественных показателей
- •8.2 Общие индексы качественных показателей
- •7.3 Индексы переменного и фиксированного состава. Индекс структурных сдвигов
- •Приложение Значение критерия Пирсона χ2
- •Приложение Значение t-критерия Стьюдента
- •Приложение Значение f-критерия Фишера при уровне значимости 0,05
- •Окончание приложения
2. Анализ вариационных рядов
2.1. Показатели вариации
Вариацией называется изменяемость, колеблемость величины признака. Вариация проявляется в отклонениях от средних и зависит от множества факторов, влияющих на социально-экономическое явление. Вариация бывает случайной и систематической, существует в пространстве и во времени. Показатели вариации делятся на абсолютные и относительные (таблица 2.1).
Таблица 2.1 - Показатели вариации
|
|
Показатель |
Формула расчета показателя | |
|
простой |
взвешенный | ||
|
Абсолютные |
Размах |
| |
|
Среднее линейное отклонение |
|
| |
|
Дисперсия |
σ2 |
| |
|
Среднее квадратическое отклонение |
|
| |
|
относительные |
Коэффициент вариации |
| |
|
Линейный коэффициент вариации |
| ||
|
Коэффициент осцилляции |
| ||
*
– Здесь fi
– частота (![]() ).
).
Относительные показатели (коэффициент вариации, линейный коэффициент вариации, коэффициент осцилляции) строятся с учетом базы (в виде средней), выражаются в процентах и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации
![]() . (2.11)
. (2.11)
Для расчета дисперсии можно использовать модифицированную формулу:
![]() . (2.12)
. (2.12)
Выведем эту формулу из формулы (2.5)
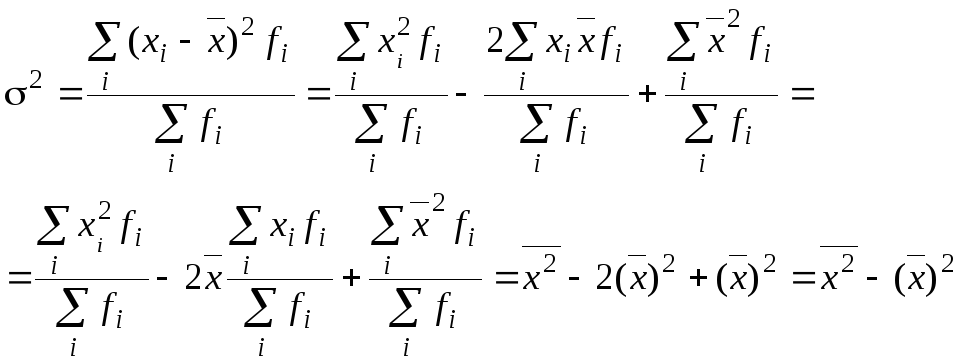
Для расчета дисперсии можно использовать способ отсчета от условного нуля, который позволяет упростить вычисления при больших значениях признака. Тогда дисперсия вычисляется по формуле:
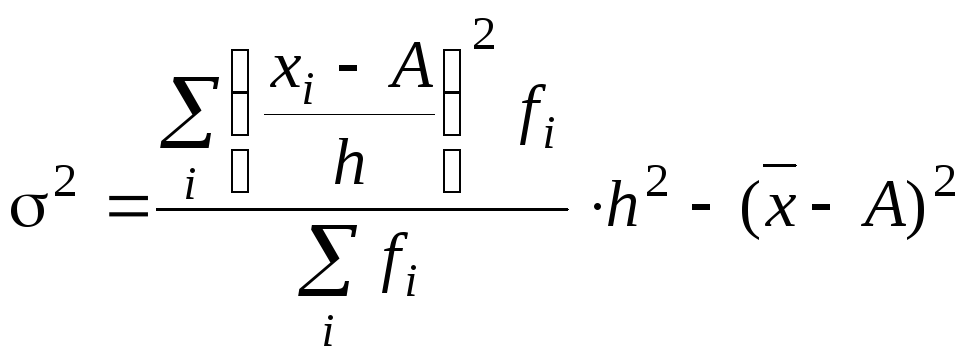 , (2.13)
, (2.13)
где h – величина интервала;
А – условный нуль, в качестве которого можно использовать как середину серединного интервала, так и середину интервала с наибольшей частотой.
2.1.1. Свойства дисперсии
Дисперсия постоянной величины равна нулю.
Если у всех значений вариантов отнять какое-то постоянное число А, то средний квадрат отклонений (дисперсия) от этого не изменится
![]() . (2.14)
. (2.14)
Это значит, что дисперсию можно вычислить не по заданным значениям признака, а по их отклонениям от какого-то постоянного числа, например условного нуля (см. формулу 2.13).
Если все значения вариантов разделить на какое-то постоянное число А, то дисперсия уменьшится в А2 раз:
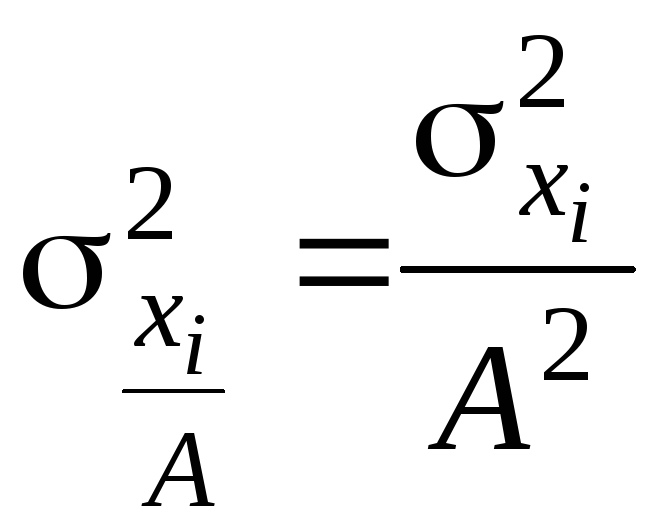 . (2.15)
. (2.15)
Если распределение признака близко к нормальному или симметричному, то по правилу мажорантности (т.к. среднее квадратическое отклонение – средняя геометрическая величина, а среднее линейное отклонение – средняя арифметическая) среднее квадратическое отклонение больше среднего линейного отклонения (
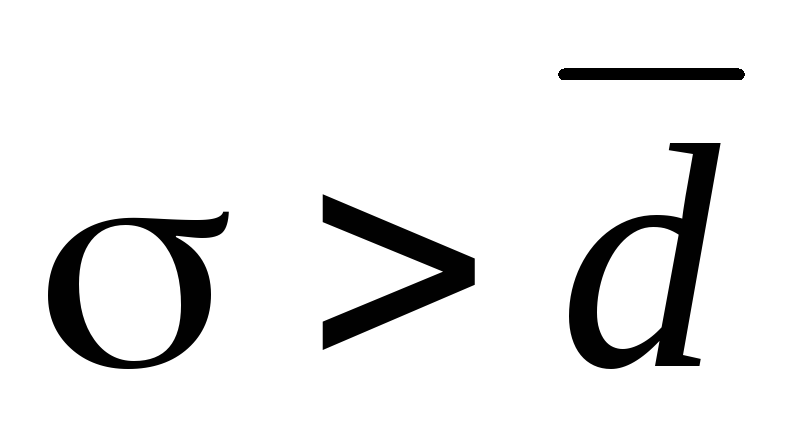 ),
причем
),
причем
![]() ,
, ![]() . (2.16)
. (2.16)
Размах вариации, среднее линейное и среднее квадратичное отклонение – это именованные величины. Единицей измерения у них и у исходных значений признака совпадают. Дисперсия может быть задана в ед.2 признака или в % отклонений.
2.1.2 Вариация альтернативного признака
Альтернативные признаки – два противоположных, взаимоисключающих друг друга качественных признака, которыми одни единицы совокупности обладают (значение варианта 1), а другие не обладают (значение варианта 0) (например, пол – мужской и женский, население – городское и сельское, продукция – годная и бракованная).
Частостью (p) является доля единиц, обладающих данным признаком, в общей численности совокупности и (q = 1 – p) – доля единиц, не обладающих данным признаком, в общей численности совокупности.
|
xi |
fi |
|
1 |
p |
|
0 |
q = 1 – p |
Средняя арифметическая альтернативного признака
![]() . (2.18)
. (2.18)
Дисперсия альтернативного признака
![]() , (2.19)
, (2.19)
т.е. дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, и доли единиц, не обладающих этим признаком.
Исходя из того, что p + q = 1:
![]() ;
; ![]() . (2.20)
. (2.20)

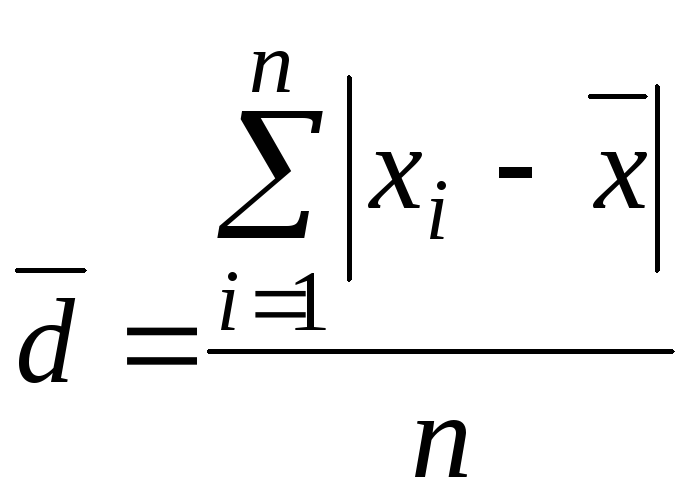 (2.2)
(2.2) *
(2.3)
*
(2.3)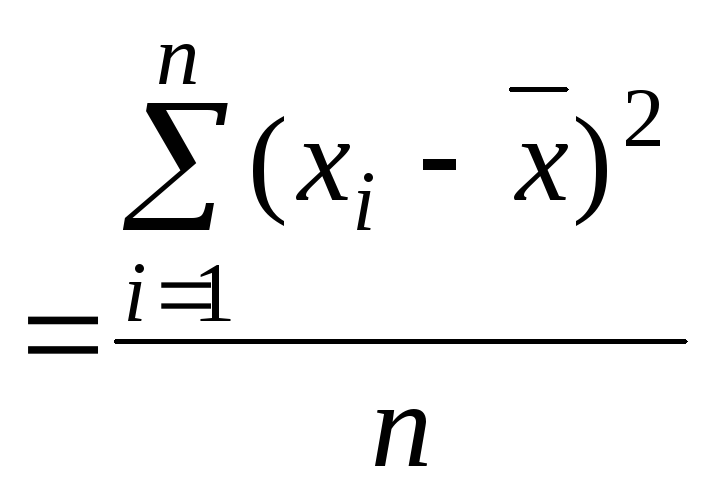 (2.4)
(2.4) (2.5)
(2.5)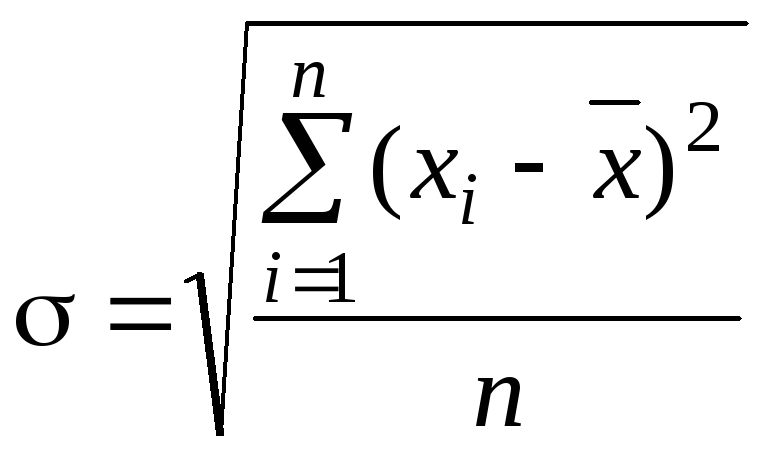 (2.6)
(2.6)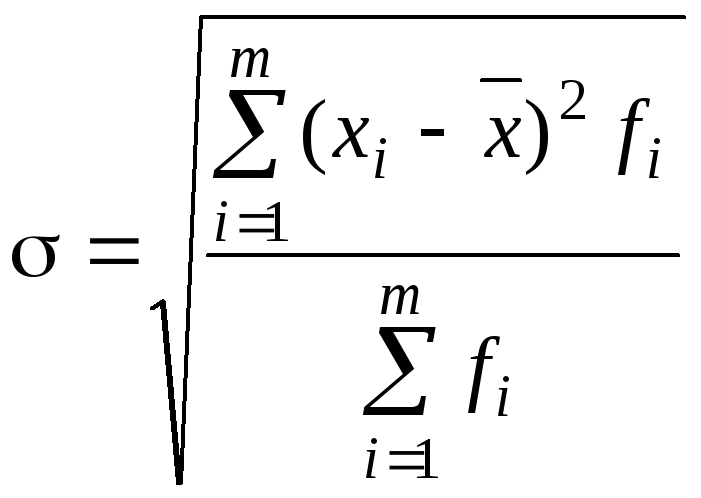 (2.7)
(2.7)