
- •Организация и функции статистических служб
- •Понятие о статистической информации
- •Статистическое наблюдение
- •Принципы построения статистических группировок
- •Вариационные ряды
- •Графическое отображение вариационных рядов
- •Пример 3.1.
- •Обобщающие статистические показатели
- •1. Средние величины
- •1.1 Средние степенные величины
- •1.2 Средние структурные величины
- •2. Анализ вариационных рядов
- •2.1. Показатели вариации
- •2.1.1. Свойства дисперсии
- •2.1.2 Вариация альтернативного признака
- •2.2. Виды дисперсий в совокупности, разделенной на части. Правило сложения дисперсий
- •3. Моменты распределения Показатели формы распределения
- •3.1. Моменты распределения
- •3.2. Показатели формы распределения
- •3.3. Теоретические кривые распределения
- •4. Выборочное наблюдение в статистике
- •4.1. Закон больших чисел и предельные теоремы
- •Выборочное наблюдение
- •4.2. Ошибка выборки для альтернативного признака
- •4.3 Определение необходимой численности выборки
- •4.4 Формы организации выборочного наблюдения
- •5. Статистические методы изучения взаимосвязи социально-экономических явлений
- •5.1 Регрессионный анализ
- •5.2 Корреляционный анализ
- •6. Ряды динамики
- •6.1 Анализ динамических рядов
- •6.2 Методы анализа тенденций рядов динамики
- •6.3 Сезонные колебания
- •6.4. Статистические методы прогнозирования экономических показателей
- •6.4.1. Прогнозирование на основе экстраполяции тренда
- •8.4.2. Выбор наилучшего тренда при прогнозировании
- •7. Экономические индексы
- •7.1 Общие индексы количественных показателей
- •8.2 Общие индексы качественных показателей
- •7.3 Индексы переменного и фиксированного состава. Индекс структурных сдвигов
- •Приложение Значение критерия Пирсона χ2
- •Приложение Значение t-критерия Стьюдента
- •Приложение Значение f-критерия Фишера при уровне значимости 0,05
- •Окончание приложения
Выборочное наблюдение
|
Наименование показателя |
Вид выборки |
|
|
|
повторная |
бесповторная |
|
Случайная выборка Средняя (стандартная) ошибка |
|
|
|
Средняя ошибка доли признака |
|
|
|
Объем выборки |
|
|
|
Типическая выборка
Средняя ошибка |
|
|
|
Объем выборки |
|
|
|
Серийная выборка
Средняя ошибка |
|
|
|
Объем выборки |
|
|
Величина
ошибки зависит от колеблемости признака
в генеральной совокупности и от объема
выборки. Т.е. чем больше вариация тем
больше ошибка, чем больше выборка, тем
меньше ошибка. Величину
![]() называют предельной ошибкой выборки.
Следовательно, предельная ошибка выборки
называют предельной ошибкой выборки.
Следовательно, предельная ошибка выборки![]() ,
т.е. предельная ошибка равнаt-кратному
числу средних ошибок выборки.
,
т.е. предельная ошибка равнаt-кратному
числу средних ошибок выборки.
t – коэффициент доверия
n– объем выборки;
N– объем генеральной совокупности;
s- число отобранных серий;
S– общее число серий;
![]() -
средняя из групповых дисперсий;
-
средняя из групповых дисперсий;
![]() -
межгрупповая дисперсия.
-
межгрупповая дисперсия.
4.2. Ошибка выборки для альтернативного признака
Теорема Бернулли утверждает, что при достаточно большом объеме выборки вероятность P расхождения между долей признака в выборочной совокупности р и долей в генеральной совокупности Pг будет стремиться к 1.
![]() , (4.10)
, (4.10)
Для
альтернативного признака среднее
квадратическое отклонение равно![]() ,
где
,
где
![]() .
Тогда средняя ошибки выборки для
альтернативного признака равна
.
Тогда средняя ошибки выборки для
альтернативного признака равна
![]() , (4.11)
, (4.11)
![]() , (4.12)
, (4.12)
Доля в генеральной совокупности Pг неизвестна и может быть только оценена при выборочном наблюдении
![]() , (4.13)
, (4.13)
При простой случайной выборке средняя квадратическая ошибки определяется по формулам:
|
Средняя квадратическая ошибка |
Повторная выборка |
Бесповторная выборка |
|
При определении среднего размера признака |
|
|
|
При определении доли признака |
|
|
4.3 Определение необходимой численности выборки
Численность
стандартной
![]() и предельной
и предельной![]() ошибки выборки связано с увеличением
объема выборкиn.
При проектировании выборочного наблюдения
заранее задается величина допустимой
ошибки
ошибки выборки связано с увеличением
объема выборкиn.
При проектировании выборочного наблюдения
заранее задается величина допустимой
ошибки
![]() и доверительная вероятность для
определения предельной ошибки
и доверительная вероятность для
определения предельной ошибки![]() .
.
Если
P=0,954,
то
![]() (2σ)
(2σ)
Если
P=0,997,
то
![]() (3σ)
(3σ)
![]() , (4.18)
, (4.18)
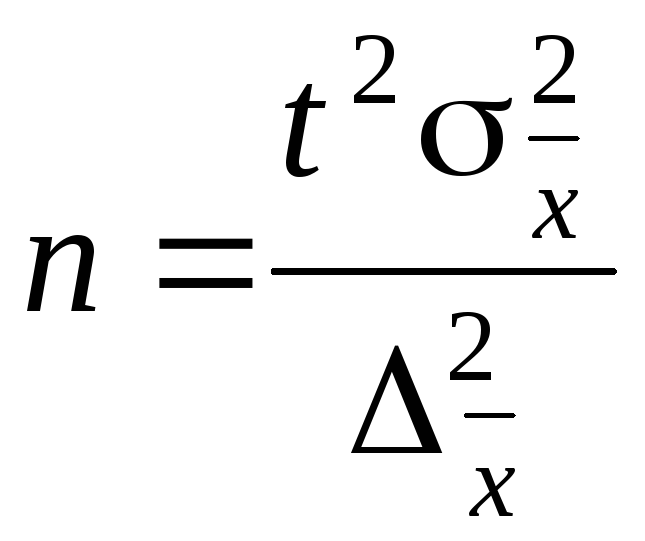 . (6.19)
. (6.19)
Для определения дисперсии признака в генеральной совокупности используются приближенные методы.
Можно провести несколько пробных обследований и по ним выбирать наибольшее значение дисперсии
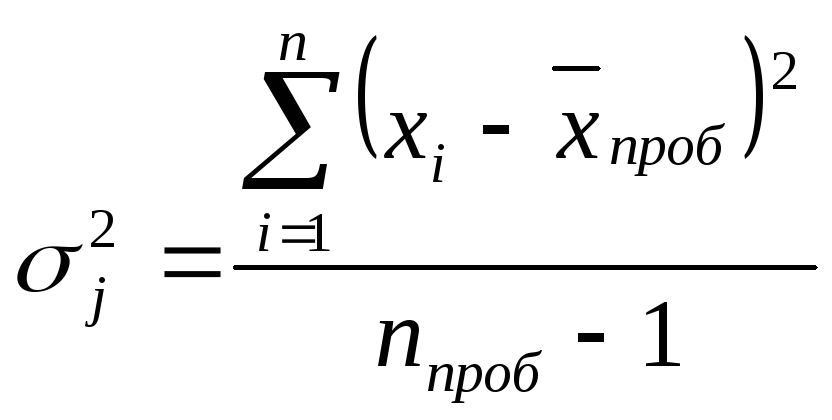 ,
где достаточно пробных наблюдений.
,
где достаточно пробных наблюдений.Можно использовать данные прошлых или аналогичных обследований.
Можно использовать размах вариации
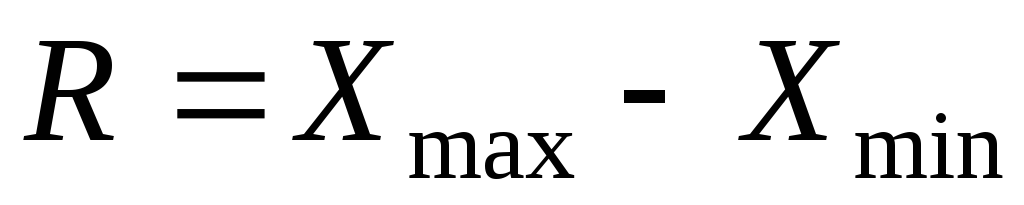 ,
если распределение нормальное, то
,
если распределение нормальное, то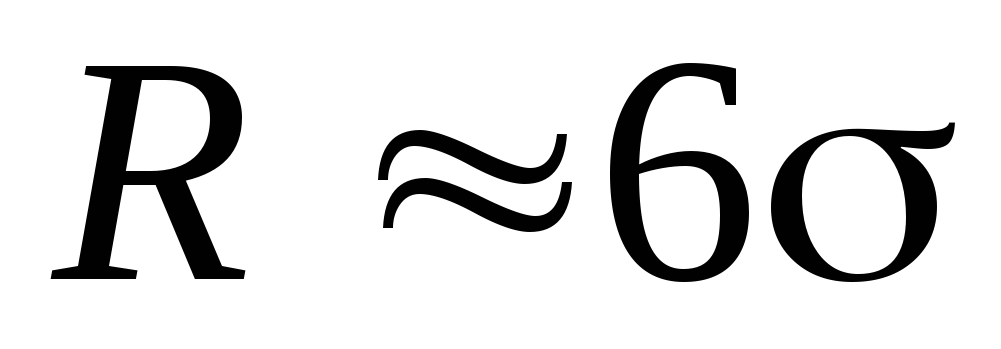 ,
т.е.
,
т.е.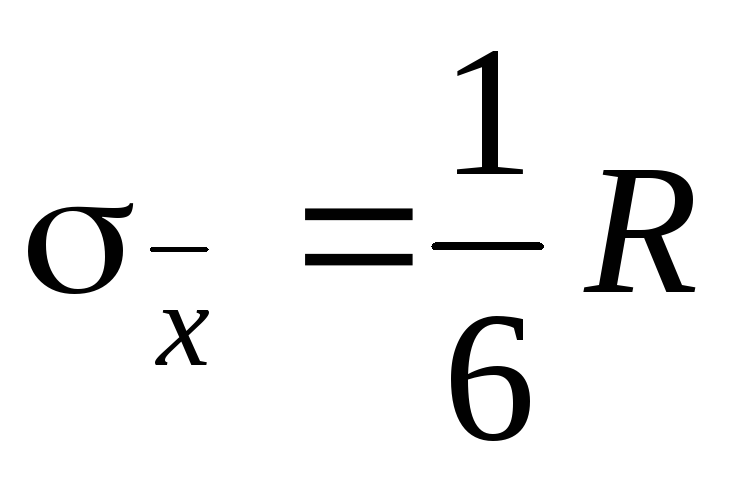 .
.
|
Объем выборки N |
Повторный отбор |
Бесповторный отбор |
|
При определении среднего размера признака |
|
|
|
При определении доли признака |
|
|
4.4 Формы организации выборочного наблюдения
Типическая (стратифицированная) выборка: общий список разбивается на отдельные списки (однородной группы). Общий объем выборки n разбивается пропорционально между списками:
1-й вариант
![]() , (4.24)
, (4.24)
где n – объем выборки
N – объем генеральной совокупности
ni – число наблюдений из i-ой типической группы
Ni – объем i-ой типической группы в генеральной совокупности.
2-й вариант – равномерный (из каждой группы поровну)
![]() , (4.25)
, (4.25)
где k – число групп.
3-й вариант – оптимальный (для групп с большей вариацией признака объем наблюдений увеличивается)
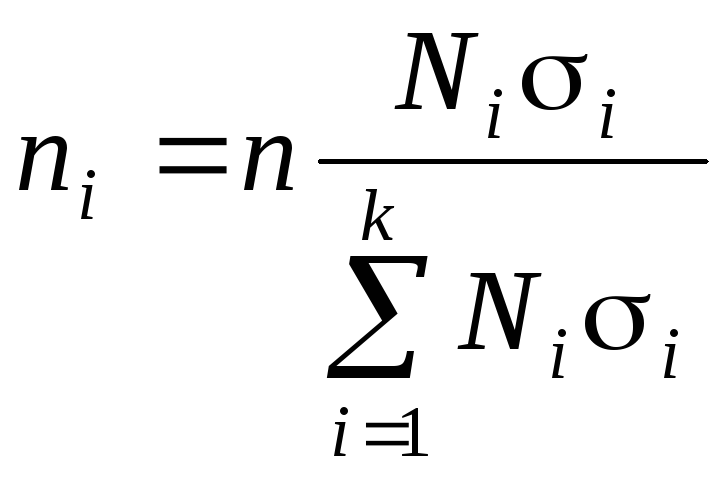 . (4.26)
. (4.26)
Серийная
(гнездовая) выборка
– в случайном порядке отбираются серии
сплошного контроля. Тогда
![]() в сериях определяется без случайной
ошибки. При равновеликих сериях
стандартная ошибка выборки определяется
в сериях определяется без случайной
ошибки. При равновеликих сериях
стандартная ошибка выборки определяется
 , (4.27)
, (4.27)
где s – число серий;
δ – межгрупповая дисперсия.
При бесповторном отборе
![]() , (4.28)
, (4.28)
где S – общее число серий в генеральной совокупности.
Механическая выборка – при ранжировании генеральной совокупности устанавливается шаг отбора в зависимости от предполагаемого % отбора. Если совокупность не ранжирована, то это случайный отбор, т.е. по известным формулам.
![]() , (4.29)
, (4.29)
Механический отбор удобен, прост и широко применяется, так при 2%-й выборке отбирается каждая 500-я единица (1:0,02), при 5%-й – каждая 20-я.
Пример
Исходя требований ГОСТа необходимо установить оптимальный размер выборки из партии изделий 2000 штук, чтобы с вероятностью 0,997 предельная ошибка не превысила 3% от веса 500 гр. Изделия (батона).
Решение.
![]() гр для средней
количественного признака
гр для средней
количественного признака
![]()
 шт.
шт.

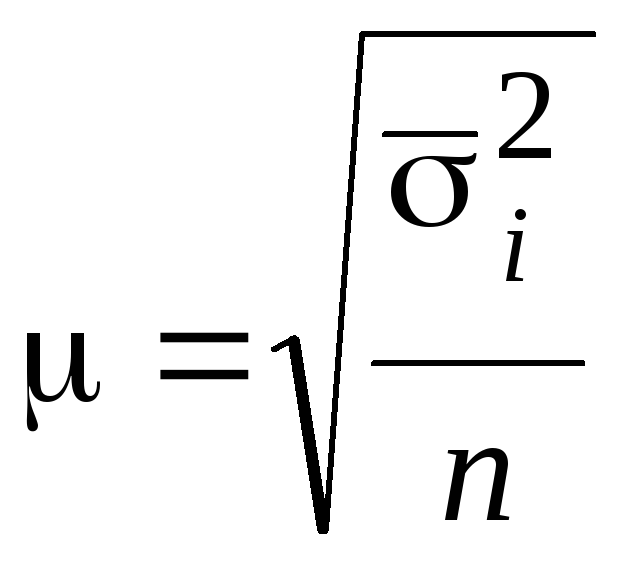
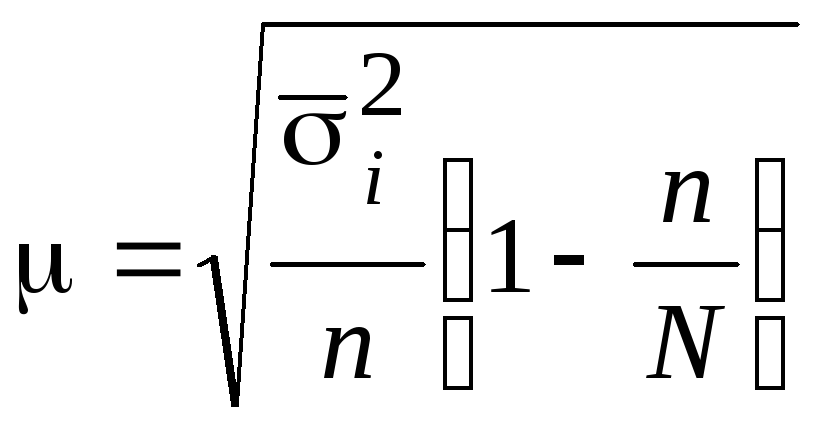
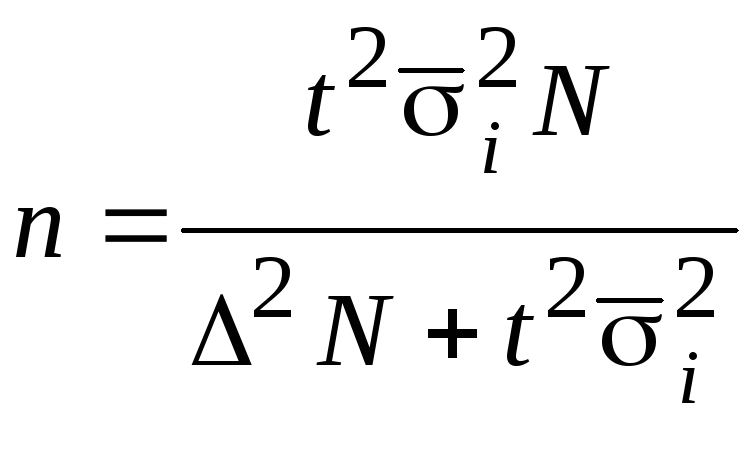
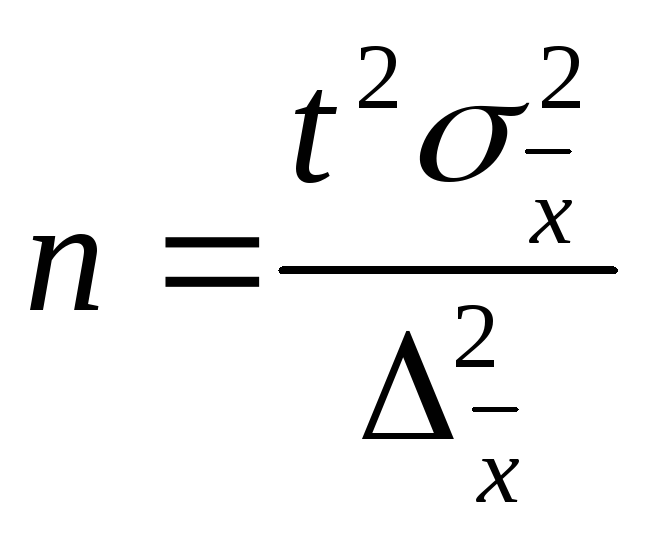 ,
(4.20)
,
(4.20)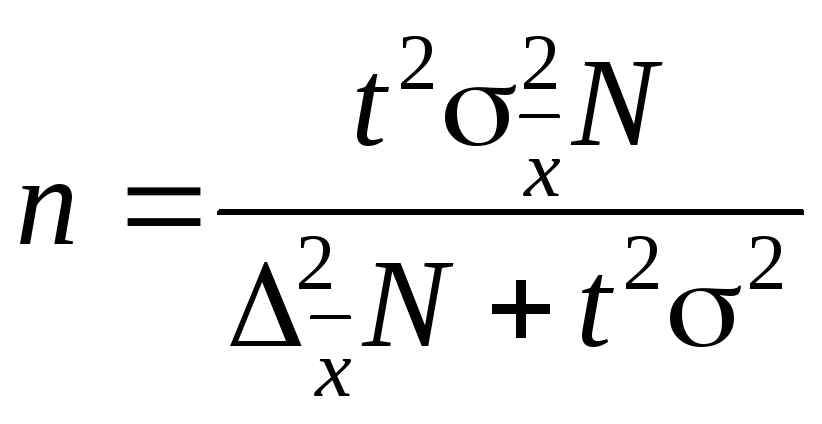 ,
(4.22)
,
(4.22)