5.1 Найдем предельную ошибку выборки.

Проведем интерполяцию: искомое значение t для заданного n или p находим по формуле:

Ошибка выборки X,Y,Z

	Число степеней свободы n	Коэффициент доверия t	Ошибка выборки	Ошибка выборки	Ошибка выборки
0,84	34	1,0345	2,3681	23,6568	8,902
0,975	34	2,1618	4,9487	49,4357	18,6026
0,9985	34	3,3033	7,5617	75,5394	28,4253

Таким образом получаем доверительные интервалы для генеральной средней выборок X, Y, Z, вычисляемые по формуле:

(аналогично для Y, Z)

Доверительные интервалы для генеральной средней ,,

	Доверит. инт.		Доверит. инт.		Доверит. инт.
0,84	18,9554	23,6916	-230,8333	-183,5197	-34,7549	-16,9509
0,975	16,3748	26,2722	-256,6122	-157,7408	-44,4555	-7,2503
0,9985	13,7618	28,8852	-282,7159	-131,6371	-54,2782	2,5724

5.2 Построим доверительные интервалы для дисперсии и стандартного отклонения генеральной совокупности с помощью распределения Пирсона.

Доверительный интервал для генеральной дисперсии вычисляется по формуле:

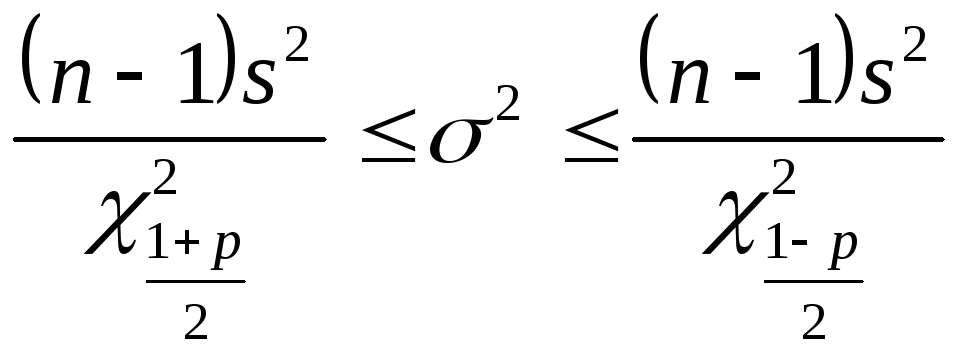
Вычислим значения и:

Вычисление значения

0,16	0,84	42,1134	25,8737
0,025	0,975	51,966	19,8062
0,0015	0,9985	63,7139	14,6136

Исходя из полученных значений, построим доверительный интервал для дисперсии генеральной совокупности:

Доверительный интервал для дисперсии генеральной совокупности

р	Интервал		Интервал		Интервал
68%	139,6098	227,2362	13932,31	22676,9633	1972,8225	3211,07
95%	113,1402	296,8485	11290,7852	29623,9028	1598,7812	4194,7603
99,70%	92,2788	402,3267	9208,9316	40150,0619	1303,9896	5685,27

Доверительный интервал для генерального С.К.О. вычисляется по формуле:

Доверительный интервал генерального С.К.О.

р	Интервал		Интервал		Интервал
68%	11,8157	15,0744	118,0352	150,5887	44,4165	56,6663
95%	10,6367	17,2293	106,2581	172,116	39,9848	64,767
99,70%	9,6062	20,0581	95,9632	200,3748	36,1108	75,4007

Задача 6.

Постройте доверительные интервалы для генерального среднего μ_X, μ_Y, μ_Z, при доверительной вероятности р=68%;95%;99,7% упрощенным способом : «одна/две/три сигмы». 1σ

Решение.

Величину коэффициента t выбираем для «стандартных» значений вероятности. Подставляем в доверительный интервал, получаем приближенные границы доверительных интервалов:

р=68%

р=95%

р=99,7%

Доверительные интервалы для генерального среднего μ_Y

P	t	μX		μY		μZ
68%	1σ	19,0344	23,6126	-230,0443	-184,3087	-34,458	-17,2478
95%	2σ	16,7452	25,9018	-252,9122	-161,4408	-43,0632	-8,6426
99,70%	3σ	14,4561	28,1909	-275,78	-138,573	-51,6683	-0,0375

Задача 7

При уровне значимости α=0,32%; 5%; 0,3% проверьте гипотезы:

σ_Х=σ_Y;

μ_X=+5;

μ_X=μ_Y;

Решение.