5 Оптимальное решение

Оптимальное решение – это совокупность n переменных (X₁, X_2,…, X_n), удовлетворяющих системе ограничений задачи, условиям неотрицательности переменных, при которой достигается максимум или минимум целевой функции или допустимое решение, при котором достигается максимальное или минимальное значение целевой функции.

Оптимальное решение может быть альтернативным. Если задача имеет несколько оптимальных решений с разным значением переменных, но с одинаковым значением целевой функции, то она имеет альтернативные оптимальные решения (альтернативный оптимум). Альтернативные решения – это допустимые решения, имеющие разное значение переменных, но равное значение целевой функции.

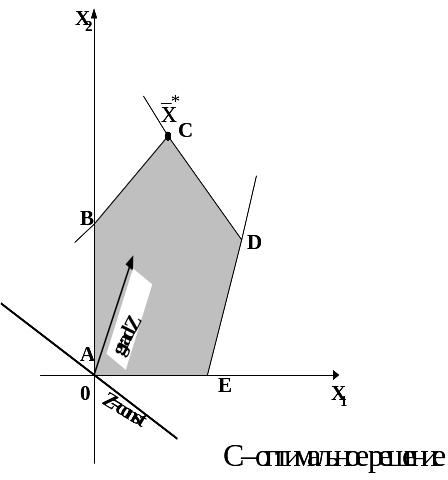
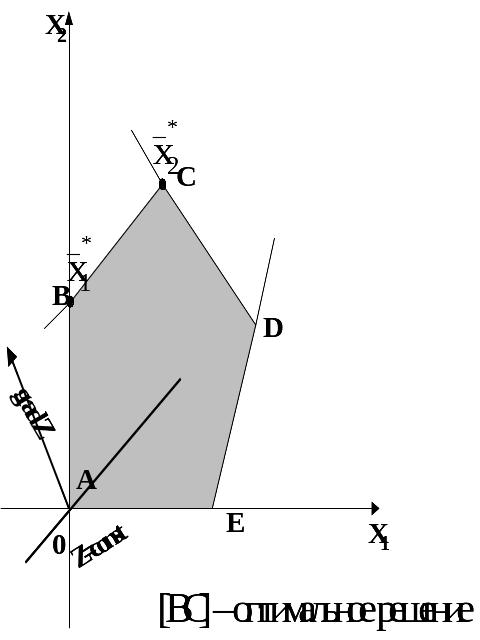
Оптимальное решение получают при перемещении линии уровня в направлении вектора-градиента до последнего соприкосновения с областью допустимых решений в точке или на отрезке.

6 Возможные варианты графического решения для двух переменных

I Область допустимых решений – ограниченная выпуклая непустая – выпуклый многоугольник

а) оптимальное решение – точка

б ) оптимальное решение – отрезок (альтернативный оптимум)

I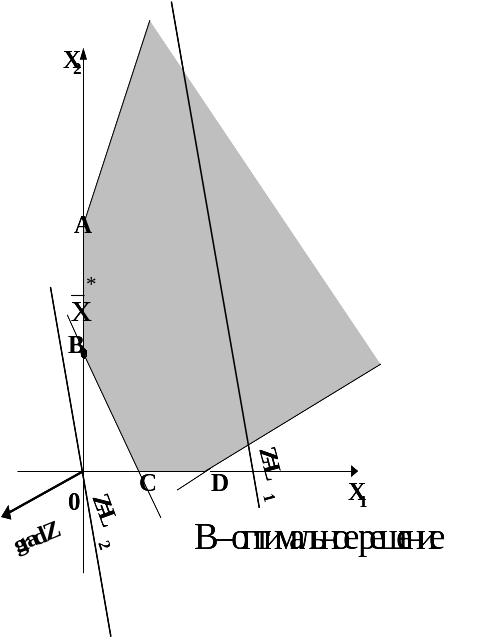 I Область допустимых решений – неограниченная непустая выпуклая область с конечным числом вершин

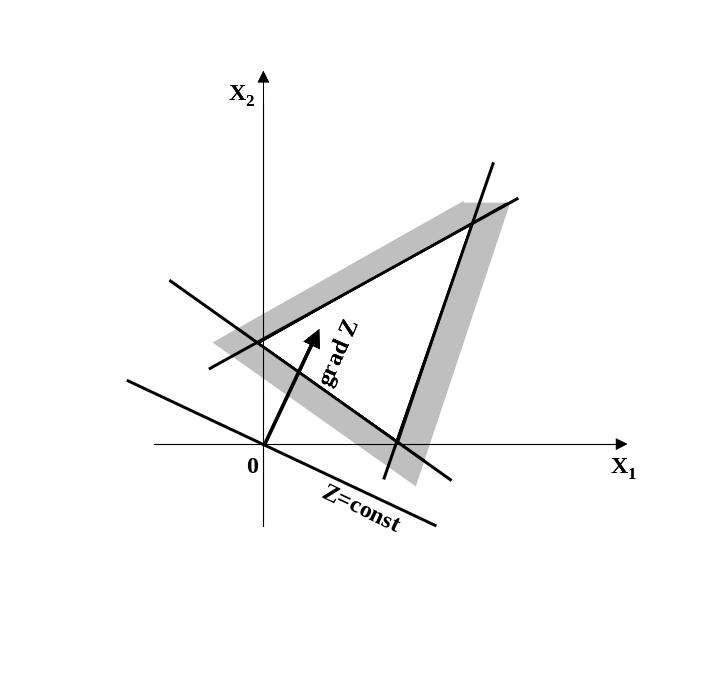
а) оптимальное решение – точка

б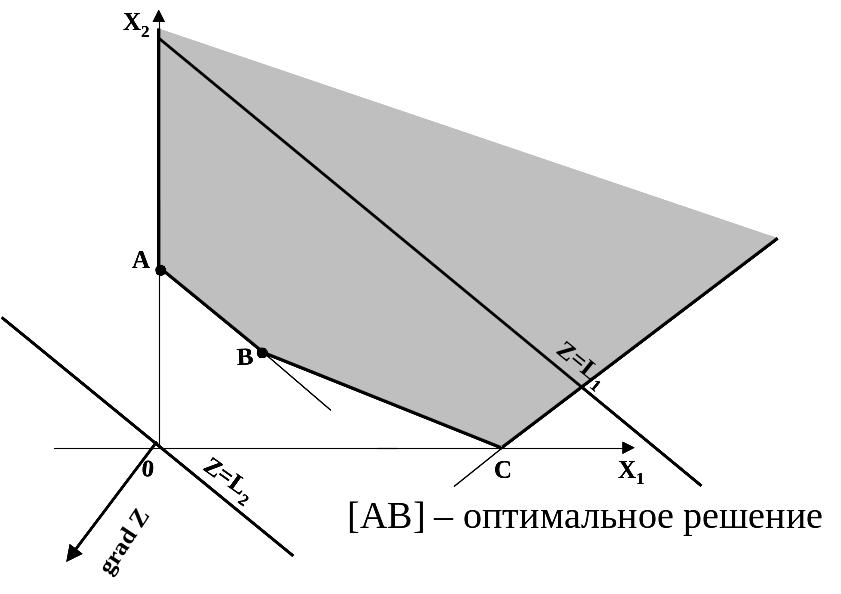 ) оптимальное решение – отрезок

в) Оптимального решения нет – целевая функция не ограничена

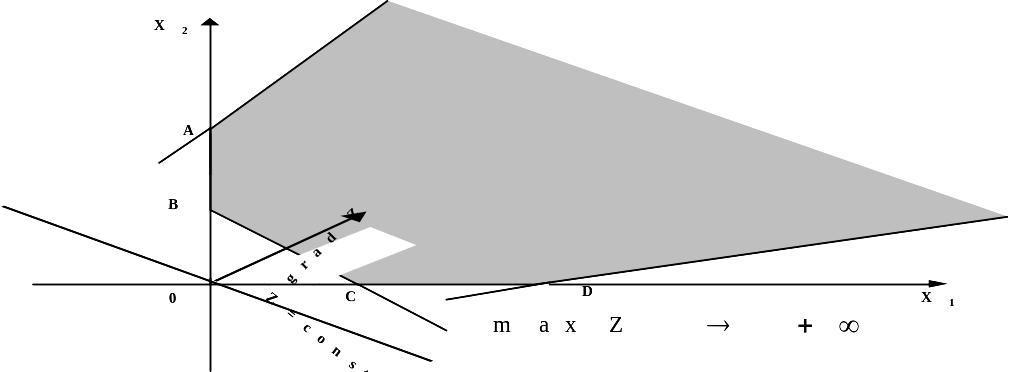
I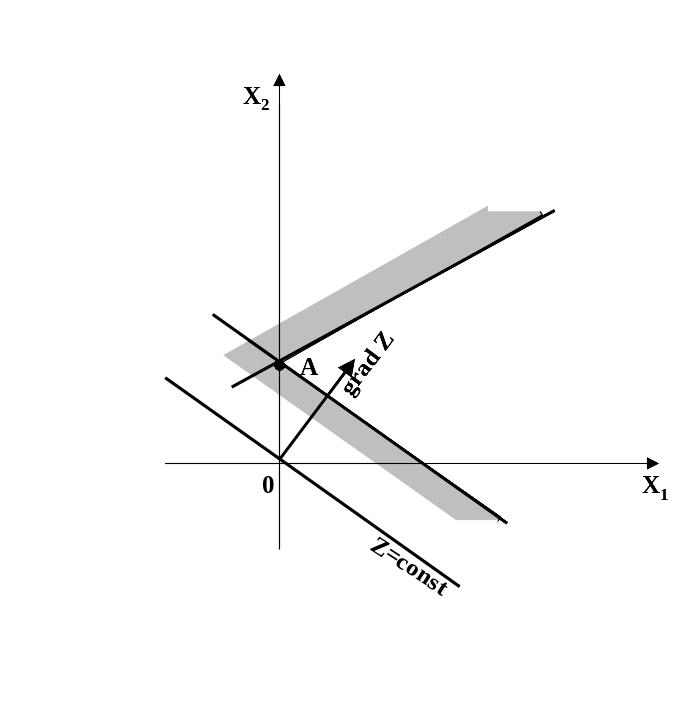 II Область допустимых решений – точка

Оптимальное решение достигается в точке области допустимых решений - единственной точке А.

IV – Область допустимых решений не существует – пустое множество

7 Соответствие понятий геометрической интерпретации при n =2, 3 и n >3

n = 2	n = 3	n > 3
ai1x1 + ai2x2 = ai0, i=1÷m, граничная прямая	ai1x1 + ai2x2 + ai3x3 = ai0, i=1÷m, граничная плоскость	ai1x1 + ai2x2 + ai3x3 + …+ ainxn = ai0, i=1÷m, граничная гиперплоскость
ai1x1 + ai2x2 ≤ ai0, i=1÷m, полуплоскость	ai1x1 + ai2x2 + ai3x3 ≤ ai0, i=1÷m, полупространство	ai1x1 + ai2x2 + ai3x3 + …+ ainxn≤ ai0, i=1÷m, полугиперплоскость
Z = с1x1 + с2x2 + с0 - линия уровня	Z = с1x1 + с2x2 + с3x3 +с0 - линия уровня –плоскость уровня	Z = с1x1 + с2x2 + …+ сnxn+с0 - линия уровня –гиперплоскость уровня
= ={с1; с2} - вектор-градиент	= = ={ с1; с2, с3}- вектор-градиент	= = ={с1;с2,…,сn}-вектор-градиент
Область допустимых решений
а) Многоугольник (выпуклая ограниченная непустая область)	а) Многогранник (выпуклая ограниченная область)
б) Неограниченная выпуклая область с конечным числом вершин	б) неограниченная выпуклая многогранная область с конечным числом вершин
в) точка	в) точка
г) пустое множество	г) пустое множество
Оптимальное решение
точка, отрезок	точка, отрезок, грань -плоскость	точка, отрезок, грань -плоскость, грань -гиперплоскость

Пример выполнения работы

Организация для производства двух видов продукции использует четыре вида производственных ресурсов: А, В, С, D.

Вид ресурса	Расход ресурсов на единицу вида продукции, ед. веса		Всего ресурсов, ед. веса
	1	2
А	1	1	6
В	2,5	4	20
С	1	2,5	10
D	1	-	5
Стоимость единицы вида продукции, ден.ед.	2	5	-

Ресурсы могут быть недоиспользованы. Найти такое соотношение производства этих видов продукции, которое обеспечит максимальный объем продукции в стоимостном выражении.

Введем обозначения.

Переменные:

X₁, ед. – количество продукции первого вида.

X₂, ед. – количество продукции второго вида.

Целевая функция:

Z, ден.ед. – максимальный объем продукции.

Запишем условия задачи в математическом виде.

Составим ограничения.

1. Баланс ресурсов вида А, ед.

X₁ + X₂ ≤ 6

[ед.] = [ед.]

2. Баланс ресурсов вида В, ед. веса

2,5X₁ + 4X₂ ≤ 20

3. Баланс ресурсов вида С, ед. веса

X₁ + 2,5X₂ ≤ 10

4. Баланс ресурсов вида D, ед. веса

X₁ ≤ 5

5. Условия неотрицательности переменных.

X₁ ≥ 0, X₂ ≥ 0

Целевая функция: max Z = 2X₁ + 5X₂

На плоскости координат строим граничные прямые и определяем полуплоскости, соответствующие ограничениям задачи.

x1	0	6
x2	6	0

1. X₁ + X₂ ≤ 6; X₁ + X₂ = 6

Точка (0,0)  полуплоскости (1*0+1*0≤6; 0 <6 – верное неравенство).

x1	0	8
x2	5	0

2. 2,5X₁ + 4X₂ ≤ 20, 2,5X₁ + 4X₂ = 20

Точка (0,0)  полуплоскости (2,5*0+4*0≤6; 0 < 20 – верное неравенство).

x1	0	10
x2	4	0

3. X₁ + 2,5X₂ ≤ 10, X₁ + 2,5X₂ = 10

Точка (0,0)  полуплоскости (1*0+2,5*0≤ 10; 0 < 10 – верное неравенство).

4. X₁ ≤ 5, X₁ = 5 – граничная прямая, параллельная оси ОX₂, проходящая через точку (5, 0); полуплоскость слева от граничной прямой, так как начало координат принадлежит полуплоскости.

5. Условия неотрицательности переменных.

X₁ ≥ 0, X₂ ≥ 0 - I четверть плоскости координат.

6. Пересечение полуплоскостей – пятиугольник ABCDE – область допустимых решений (ОДР) (рис. 1)

7. Линия уровня.

max Z = 2X₁ + 5X₂ - прямая уровня.

Пусть Z = const, например Z = 0, тогда 2X₁ + 5X₂ = 0

x1	0	5
x2	0	-2

8. Вектор-градиент =

= {2,5}. Начало координат – начало вектора-градиента, точка (2,5) – конец вектора-градиента. Вектор-градиент показывает направление перемещения линия уровня в направлении максимизации целевой функции.

(2)

Рисунок (1) графического решения задачи

9. Оптимальное решение.

Оптимальное решение получаем, перемещая линию уровня в направлении вектора-градиента до последнего соприкосновения с областью допустимых решений. У нас получается отрезок прямой (3).[BC] –оптимальное альтернативное решение. Координаты точки В(0,4); координаты точки С получаем из решения системы уравнений:

X₁ + X₂ = 6 и

X₁ + 2,5X₂ = 10

Экстремальное значение целевой функции: Z(B) = 2*0+5*4=20 (ден.ед.)

Z(С) = (ден.ед.)

Ответ: Область допустимых решений - непустая ограниченная выпуклая - многоугольник ABCDE. Оптимальное решение достигается на отрезке [BC].

Первое решение - В(0,4).

Переменные:

X₁=0 ед. – количество продукции первого вида.

X₂ =4 ед. – количество продукции второго вида.

Целевая функция:

maxZ=20 ден.ед. – максимальный объем продукции.

Второе решение - С .

Переменные:

X₁= ед. – количество продукции первого вида.

X₂ = ед. – количество продукции второго вида.

Целевая функция:

maxZ=20 ден.ед. – максимальный объем продукции

Список индивидуальных данных

Задание

а) Используя однородные формы записи задач линейного программирования, полученные в лабораторной работе 2, решить эти задачи графическим методом. Сравнить значения целевых функций для эквивалентных однородных форм с разным набором сочетаний свободных переменных (значение k – меняется по указанию преподавателя).

1. max Z = 5·x₁ + 3·x₂ + 4·x₃ + х₄

2. max Z = 3·x₁ + 4·x₂ + 5·x₃ + 2·х₄

3. max Z = 2·x₁ + 3·x₂ + 4·x₃ - 5·х₄

4. max Z = 3·x₁ + 5·x₂ - 6·x₃ + 7·х₄

5. max Z = 6·x₁ + 7·x₂ + 3·x₃ + 2·х₄

6. max Z = x₁ + x₂ + x₃ + х₄

7. max Z = 2·x₁ + 5·x₂ - 3·x₃ + 6·х₄

8. max Z = 3·x₁ + 2·x₂ + 6·x₃ + 4·х₄

9. max Z = 8·x₁ + 3·x₂ + 4·x₃ + 5·х₄

10. max Z = - x₁ + 3·x₂ + 4·x₃ - 2·х₄

11. max Z = -3·x₁ - 3·x₂ + x₃ + 5·х₄

12. max Z = 7·x₁ + 2·x₂ - 3·x₃ + 4·х₄

13. max Z = 2·x₁ - 3·x₂ + 4·x₃ + х₄

14. max Z = x₁ - 4·x₂ + 5·x₃ - 6·х₄

15. max Z = 4·x₁ + 2·x₂ + 6·x₃ + х₄

16. max Z = 2·x₁ - x₂ - 3·x₃ + 5·х₄

б) Составить по образцу условия семи задач линейного программирования, имеющих разные варианты решения, и решить графически.

1. 3х₁+2х₂6

2х₁+3х₂6

х₁ ≥ 0, х₂ ≥ 0

maxZ=5х₁+3х₂+6

2. 3х₁+2х₂6

2х₁+3х₂6

х₁ ≥ 0, х₂ ≥ 0

maxZ=3х₁+2х₂+6

3. 3х₁-2х₂6

2х₁-3х₂6

х₁ ≥ 0, х₂ ≥ 0

maxZ=-3х₁+2х₂+6

4. 3х₁+2х₂6

- х₁-2х₂-6

х₁ ≥ 0, х₂ ≥ 0

maxZ=3х₁+2х₂+6

5. -3х₁-2х₂-6

-2х₁-3х₂-6

х₁ ≥ 0, х₂ ≥ 0

maxZ=-3х₁-2х₂+6

6.- 3х₁+2х₂6

- 2х₁+3х₂6

х₁ ≥ 0, х₂ ≥ 0

maxZ=-3х₁ -4х₂+6

7. х₁+х₂3

-х₁-х₂-6

х₁ ≥ 0, х₂ ≥ 0

maxZ=3х₁+2х₂+6

Контрольные вопросы

1. Какое решение называется допустимым?

2. Какое решение называется альтернативным?

3. Какое решение называется оптимальным?

4. Какова область решений, удовлетворяющих линейному ограничению неравенству с двумя переменными?

5. Какова область допустимых решений, удовлетворяющих линейному ограничению неравенству с тремя переменными?

6. Какова область допустимых решений задачи линейного программирования с двумя переменными?

7. Что показывает вектор-градиент?

8. Найти вектор-градиент, если max Z= C₁X₁+C₂X₂+C₀?

9. Как расположены линия уровня и вектор градиент?

10. Сколько линий уровня можно построить в одной задаче?

11. Как расположены линии уровня в одной задаче?

12. Что является оптимальным решением задачи линейного программирования с двумя переменными?

13. Что является оптимальным решением задачи линейного программирования с тремя и более переменными?

14. Каков геометрический смысл линейного ограничения неравенства с двумя переменными, замененного равенством?

15. Каков геометрический смысл линейного ограничения неравенства с тремя переменными?

16. Каков геометрический смысл линейного ограничения неравенства с n переменными?

17. Каков геометрический смысл линейной целевой функции с двумя переменными?

18. Каков геометрический смысл линейной целевой функции с тремя переменными?

19. Каков геометрический смысл линейной целевой функции с n переменными?

20. Может ли быть точка Х(-3;-2) допустимым решением задачи линейного программирования?

21. Может ли быть точка Х(-5;2) допустимым решением задачи линейного программирования?

22. Может ли быть точка Х(7;-3) допустимым решением задачи линейного программирования?

23. Может ли быть точка Х(3;5) допустимым решением задачи линейного программирования?