5 Решение задач на основе фундаментальной теоремы

Пример. Решить задачу графическим методом. Найти оптимальное решение на основе фундаментальной теоремы линейного программирования (среди опорных решений). Каждому опорному решению поставить в соответствие вершину области допустимых решений.

4х₁ + х₂ ≤ 6 (I)

-3х₁ + 2х₂ ≤ 6 (II)

х₁ ≤ 1 (III)

х₁  0, х₂  0, (IV)

max Z =х₁ + х₂

1.Графически находим область допустимых решений задачи.

Областью допустимых решений является ограниченный выпуклый многоугольник ОАВСД. Вершины имеют координаты О(0;0), А(0;3), С(1;2), Д (1;0). Оптимальное решение достигается в точке В, максимум целевой функции равен

Введя в ограничения дополнительные переменные, перейдем от однородной формы задачи к канонической форме. Получим:

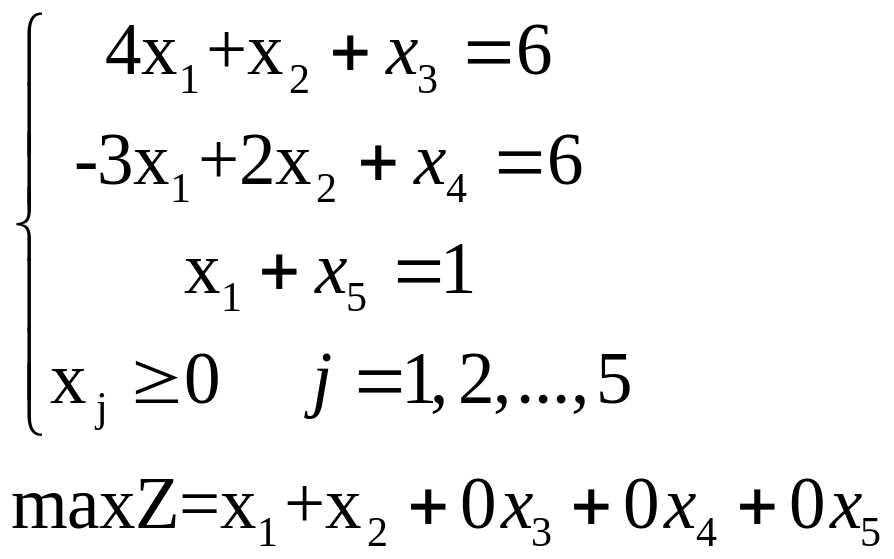
Система имеет единичную подматрицу и неотрицательные свободные члены. Поэтому к этой системе применимы симплексные преобразования однократного замещения. Преобразуем целевую функцию (перенося все переменные в левую часть), получим:

Z -х₁ - х₂ + 0х₃+0х₄+ 0х₅ = 0

Заполним исходную таблицу.

Таблица 1

П Б Z x1 x2 x3 x4 x5 ai0 К∑ Опорное решение x3 0 4 1 1 0 0 6 12 6/4=3/2 x4 0 -3 2 0 1 0 6 6 - Z1=0 x5 0 1 0 0 0 1 1 3 1/1=1 i* O(0;0) Z 1 -1 -1 0 0 0 0 -1 X

j*

Составляем все возможные сочетания базисных переменных в опорных решениях. Поэтому в задаче не более десяти опорных решений Х₁ Х₂ Х₃; Х₁ Х₂ Х₄; Х₁ Х₂ Х₅; Х₁ Х₃ Х₄; Х₁ Х₃ Х₅; Х₁ Х₄ Х₅; Х₂ Х₃ Х₄; Х₂ Х₃ Х₅; Х₂ Х₄ Х₅; Х₃ Х₄ Х₅. Сочетание Х₃ Х₄ Х₅ записано в первой таблице. В качестве разрешающего столбца выберем столбец переменной Х_1. Минимальное симплексное отношение определяет разрешающую строку – это третья строка системы. Поэтому переменная Х₅ выйдет из базиса, а на ее место войдет переменная Х₁ . Получим сочетание Х₁ Х₃ Х₄, порядок переменных в базисе роли не играет, так как перестановка местами ограничений системы является эквивалентным преобразованием.

Исходное опорное решение , значение целевой функции Z₁ = 0 и вершина, соответствующая этому опорному решению, записаны в последнем столбце таблицы.

Таблица 2

П Б Z x1 x2 x3 x4 x5 ai0 К∑ Опорное решение x3 0 0 1 1 0 -4 2 0 2/1=2 i* x4 0 0 2 0 1 3 9 15 9/2=4,5 Z2=1 x1 0 1 0 0 0 1 1 3 - D(1;0) Z 1 0 -1 0 0 1 1 2 X

j*

Таблица 3

П Б Z x1 x2 x3 x4 x5 ai0 К∑ Опорное решение x2 0 0 1 1 0 -4 2 0 - Z3=3 x4 0 0 0 -2 1 11 5 15 5/11 i* x1 0 1 0 0 0 1 1 3 1/1=1 Z 1 0 0 1 0 -3 3 2 X

j*

Таблица 4

П Б Z x1 x2 x3 x4 x5 ai0 К∑ Опорное решение x2 0 0 1 0 Z4= x5 0 0 0 1 - x1 0 1 0 0 6/2=3 i* Z 1 0 0 0 X

j*

Таблица 5

П Б Z x1 x2 x3 x4 x5 ai0 К∑ Опорное решение x2 0 1 0 0 3 3 Z5=3 x5 0 1 0 0 0 1 1 3 x3 0 0 1 0 3 9 А (0;3) Z 1 0 0 0 3 2 X

Данная задача имеет только пять опорных решений, которые записаны в таблицах 1 – 5. Сравним все значения целевой функции и выберем среди них оптимальное. Максимум целевой функции равен максимальному значению из пяти чисел: (0; 1; 3; ; 3). Следовательно, , ему соответствует оптимальное решение и вершина области допустимых решений.

Пример выполнения работы

Организация для производства двух видов продукции использует два вида производственных ресурсов: А, В.

Вид ресурса	Расход ресурсов на единицу вида продукции, ед. веса		Всего ресурсов, ед. веса
	1	2
А	1	1	6
В	1	2,5	10
Стоимость единицы вида продукции, ден.ед.	2	5	-

Ресурсы могут быть недоиспользованы. Найти такое соотношение производства этих видов продукции, которое обеспечит максимальный объем производства продукции в стоимостном выражении.

I) Запишем условия задачи в математическом виде.

Обозначения:

Переменные.

Х₁, ед. - количество продукции 1-го вида,

Х₂, ед. - количество продукции 2-го вида.

Целевая функция.

Z,ден.ед. - максимальный объём продукции.

Запишем условия задачи в математическом виде.

Составим ограничения.

1. Баланс ресурсов вида А, ед.

X₁ + X₂ ≤ 6

[ед.] = [ед.]

2. Баланс ресурсов вида В, ед. веса

X₁ + 2,5X₂ ≤ 10

3. Условия неотрицательности переменных.

X₁ ≥ 0, X₂ ≥ 0

Целевая функция: max Z = 2X₁ + 5X₂

II) Решим задачу графическим методом.

На плоскости координат строим граничные прямые и определяем полуплоскости, соответствующие ограничениям задачи.

x1	0	6
x2	6	0

1. X₁ + X₂ ≤ 6; X₁ + X₂ = 6

Точка (0,0)  полуплоскости (1*0+1*0≤6; 0 <6 – верное неравенство).

x1	0	10
x2	4	0

2. X₁ + 2,5X₂ ≤ 10, X₁ + 2,5X₂ = 10

Точка (0,0)  полуплоскости (1*0+2,5*0≤ 10; 0 < 10 – верное неравенство).

3. Условия неотрицательности переменных.

X₁ ≥ 0, X₂ ≥ 0 - I четверть плоскости координат.

4. Пересечение полуплоскостей – пятиугольник ABCD – область допустимых решений (ОДР) (рис. 3)

5. Линия уровня.

max Z = 2X₁ + 5X₂ - прямая уровня.

Пусть Z = const, например Z = 0, тогда 2X₁ + 5X₂ = 0

X1	0	5
X2	0	-2

6. Вектор-градиент =

= {2,5}. Начало координат – начало вектора-градиента, точка (2,5) – конец вектора-градиента. Вектор-градиент показывает направление перемещения линия уровня в направлении максимизации целевой функции.

Р

ис.3

7. Оптимальное решение.

Оптимальное решение получаем, перемещая линию уровня в направлении вектора-градиента до последнего соприкосновения с областью допустимых решений. У нас получается отрезок прямой (2).[BC] –оптимальное альтернативное решение. Координаты точки В(0,4); координаты точки С получаем из решения системы уравнений:

X₁ + X₂ = 6 и

X₁ + 2,5X₂ = 10

Экстремальное значение целевой функции: Z(B) = 2*0+5*4=20 (ден.ед.)

Z(С) = (ден.ед.)

Ответ: Область допустимых решений - непустая ограниченная выпуклая - многоугольник ABCD. Оптимальное решение достигается на отрезке [BC].

Первое решение - В(0,4).

Переменные:

X₁=0 ед. – количество продукции первого вида.

X₂ =4 ед. – количество продукции второго вида.

Целевая функция:

maxZ=20 ден.ед. – максимальный объем продукции.

Второе решение - С .

Переменные:

X₁= ед. – количество продукции первого вида.

X₂ = ед. – количество продукции второго вида.

Целевая функция:

maxZ=20 ден.ед. – максимальный объем продукции

III) Решим задачу на основе фундаментальной теоремы линейного программирования.

Запишем каноническую форму задачи.

1. X₁ + X₂ +X₃= 6,

где X₃, ед. веса - недоиспользование ресурсов вида А,

2. X₁ + 2,5X₂ +X₄=10,

где X₄, ед. веса - недоиспользование ресурсов вида В.

3. Условия неотрицательности переменных.

X_j ≥ 0, j=1÷ 4

Целевая функция: max Z = 2X₁ + 5X₂ +0X₃+0X₄

Преобразуем целевую функцию, получим Z -2X₁ - 5X₂ +0X₃+0X₄=0.

Каноническую форму задачи с преобразованной целевой функцией

1. X₁ + X₂ +X₃= 6,

2. X₁ + 2,5X₂ +X₄=10,

3. X_j ≥ 0, j=1÷ 4

Z -2X₁ - 5X₂ +0X₃+0X₄=0

запишем в таблицу Гаусса, так как задача приведена к единичному базису (X₃ X_4,) с неотрицательными значениями базисных переменных.

Таблица 1

Баз.\Пер.	Z	X1	X2	X3	X4	ai0	kΣ	ai0≥0/ aij*>0	Опорное реш-е
X3	0	1	1	1	0	6	9	6:1=6	X(0;0;6;10)	I*
X4	0	1	2,5	0	1	10	14,5	10:1=10	Z=0
Z	1	-2	-5	0	0	0	-5	x	A(0;0)
		J*

Таблица 2

Баз.\Пер.	Z	X1	X2	X3	X4	ai0	kΣ	ai0≥0/ aij*>0	Опорное реш-е
X1	0	1	1	1	0	6	9	6:1=6	X(6;0;0;4)
X4	0	0	1,5	-1	1	4	5,5	4:1,5=8/3	Z=12	I*
Z	1	0	-3	2	0	12	12	x	D(6;0)
			J*

Таблица 3

Баз.\Пер.	Z	X1	X2	X3	X4	ai0	kΣ	ai0≥0/ aij*>0	Опорное реш-е
X1	0	1	0	5/3	-2/3	10/3	16/3	10/3:5/3=2	X(10/3;8/3;0;0)	I*
X2	0	0	1	-2/3	2/3	8/3	11/3	-	Z=20
Z	1	0	0	0	-2	20	19	x	C (10/3;8/3)
				J*

Таблица 4

Баз.\Пер.	Z	X1	X2	X3	X4	ai0	kΣ	ai0≥0/ aij*>0	Опорное реш-е
X3	0	0,6	0	1	-0,4	2	3,3	-	X(0;4;2;0)
X2	0	0,4	1	0	0,4	4	5,8	-	Z=20
Z	1	0,6	0	0	-2	20	19	x	B (0;4)

Все опорные решения перебрали. Новых получить нельзя. Выбираем оптимальное опорное решения по максимальному значению Z.

max Z= max{0; 12; 20; 20}=20.

Получили два опорных решения с максимальным значением Z, равным 20. Оба опорных решения являются оптимальными: X*(10/3;8/3;0;0) и X*(0;4;2;0). Задача имеет альтернативный оптимум. Max Z=20. Этим оптимальным опорным решениям соответствуют вершины C (10/3;8/3) и B (0;4).

Ответ. Максимум производства продукции равен 20 денежным единицам. Задача имеет альтернативный оптимум: оптимальное решение X*(10/3;8/3;0;0), которому соответствует вершина C (10/3;8/3), и оптимальное решение X*(0;4;2;0), которому соответствует вершина B (0;4).

Первое оптимальное решение достигается при производстве первого вида продукции в количестве 10/3 единиц, а второго вида продукции в количестве 8/3 единиц. Все ресурсы используются полностью (X₃=X₄=0).

Второе оптимальное решение достигается при производстве первого вида продукции в количестве 0 единиц, а второго вида продукции в количестве 4 единиц. При этом первый вид ресурса не используется полностью, часть его в количестве 2 единиц не используется (X₃=2), а второй вид ресурса используется полностью (X₄=0).

Список индивидуальных данных

Организация для производства двух видов продукции использует два вида производственных ресурсов: А, В.

Вид ресурса	Расход ресурсов на единицу вида продукции, ед.*		Всего ресурсов, ед.
	1	2
А	а11	а12	а10
В	а21	а22	а20
Стоимость единицы вида продукции, ден.ед.	С1	С2	-

*) Если коэффициент при какой-либо переменной отрицательный, то предполагается, что соответствующий ресурс в данном процессе производится, а не расходуется.

Ресурсы могут быть недоиспользованы. Найти такое соотношение производства этих видов продукции, которое обеспечит максимальный объем производства продукции в стоимостном выражении.

Задачу линейного программирования: 1) записать в однородной (исходной) форме (правила записи смотрите в лабораторной работе 1).

2). Решить графическим методом. Записать ответ с экономическим содержанием

3). Решить на основе фундаментальной теоремы, то есть перейти от однородной формы к канонической, преобразовать целевую функцию, записать исходное опорное решение с преобразованной целевой функцией в таблицу Гаусса, выполнить симплексные преобразования однократного замещения, выписать опорное решение и значение целевой функции, найти оптимальное решение среди всех опорных решений, сравнив значения целевых функций и выбрав среди них максимальное. Каждому опорному решению поставить в соответствие вершину области допустимых решений, полученную графическим методом.

Вариант	а11	а12	а10	а21	а22	а20	С1	С2	С0
1	1	2	3	1	1	1	1	2	4
2	2	4	8	2	2	4	2	1	3
3	-1	1	2	1	2	10	1	3	5
4	1	2	3	2	1	3	1	1	2
5	-2	3	6	3	-2	12	4	3	1
6	3	4	12	3	-4	8	2	5	4
7	1	2	4	2	-2	6	3	1	4
8	2	-1	6	1	4	4	1	1	5
9	1	4	8	1	2	4	1	6	3
10	2	1	4	1	2	4	1	1	-2
11	1	1	4	2	1	2	1	2	1
12	2	1	6	1	1	4	1	2	4
13	1	1	5	-1	1	3	2	4	1
14	-1	1	2	2	1	8	1	-3	3
15	2	1	5	2	-3	6	3	6	1
16	1	-1	2	2	1	6	1	1	-3
17	7	2	7	4	-2	2	1	2	2
18	-1	2	2	1	1	4	1	3	5
19	1	1	4	2	-1	3	1	1	-3
20	2	1	4	3	2	6	1	5	2
21	1	-1	2	2	3	9	2	1	-1
22	3	-4	6	1	2	4	2	3	-2
23	2	3	6	2	1	2	1	3	4
24	2	3	6	1	2	2	2	1	6
25	3	1	6	1	1	4	2	1	5
26	2	3	6	1	2	4	1	1	3
27	1	1	2	2	1	1	1	2	1
28	1	-1	1	2	1	4	1	1	-2
29	1	1	10	3	-1	5	1	4	9
30	2	5	10	2	1	6	3	-1	3
31	2	3	6	3	2	6	1	2	-3

Контрольные вопросы

1. Дайте определение граничной прямой.

2. Дайте определение области допустимых решений.

3. Дайте определение линии уровня и вектора-градиента.

4. Возможные варианты графического решения задач Л.П.

5. Дайте определение базисного, опорного и оптимального решений.

6. Всегда ли существует взаимно однозначное соответствие между опорными решениями и вершинами (крайними, угловыми) точками области допустимых решений?

7. Сформулируйте фундаментальную теорему линейного программирова­ния.

8. Фундаментальная теорема для ограниченной области допустимых решений (ОДР).

9. Показать справедливость фундаментальной теоремы для неограниченной области допустимых решений (ОДР).

10. Обобщенная фундаментальная теорема.

11. Что такое симплексное отношение?

12. Могут ли быть отрицательными свободные члены при симплексных преобразованиях однократного замещения?

13. Какие переменные и как замещаются при симплексных преобразованиях однократного замещения?

14. Где и как найти значение базисных переменных в таблицах при симплексных преобразованиях однократного замещения?

15. Чему равны свободные переменные в таблицах при симплексных преобразованиях однократного замещения?