Эквивалентность различных форм задач линейного программирования

Две формы записи задачи линейного программирования эквивалентны, если любому допустимому решению одной из них соответствует единственное допустимое решение другой и при этом целевые функции обеих задач равны.

Две формы записи задачи линейного программирования эквивалентны, если оптимальному решению одной задачи соответствует оптимальное решение другой задачи и при этих оптимальных решениях значения целевых функций равны.

Пусть Хи(х ₁⁰, х ₂⁰ ,…, х _n⁰); Хк(х ₁⁰, х ₂⁰ ,..., х _n⁰, х _n+1⁰). Хи ~ Х к - эквивалентные допустимые решения исходной и канонической форм. При этом Z(Хи) = Z(Хк).

Пусть Хи(х ₁^*, х ₂^* ,…, х _n^*); Хк(х ₁^*, х ₂^* ,..., х _n^*, х _n+1^*). Хи^*~ Х к^* -

эквивалентные оптимальные решения исходной и канонической форм задачи линейного программирования. Тогда Z(Хи^*) = Z(Хк^*). Z(Хи^*)  Z(Хи). Z(Хк^*)  Z(Хк) (при решении на максимум Z).

Если две задачи линейного программирования эквивалентны, то достаточно найти оптимальное или хотя бы допустимое решение только в одной форме записи задачи. Решение в другой форме можно записать без повторного решения задачи в этой форме, а пользуясь лишь правилами соответствия.

Правило перехода от одной формы к другой обеспечивает эквивалентность задач.

Задача линейного программирования, записанная в исходной форме, эквивалентна как задаче, записанной в канонической форме, так и задаче, записанной в однородной форме.

Общая постановка задачи

Дана задача в канонической форме:

max Z = C₁*x₁  + C₂*x₂ +...+ C_n*x _n+ C₀

a ₁₁ x ₁ + a ₁₂ x ₂ +...+ a _1n. x _n = a ₁₀

a ₂₁ x ₁ + a ₂₂  x₂  +...+ a _2n  x _n  = a ₂₀

......................................................................

a _{m 1} x ₁  + a _{m 2} x₂ +...+ a _{m n} x _n= a _{m 0}

x j ≥ 0 , j = 1 n.

С помощью преобразований Жордана - Гаусса получить каноническую форму с единичным базисом (случай 1), а затем получить задачу в однородной форме:

max Z = C`<sub>1</sub> *x<sub>1</sub>  + C`₂*x₂ +...+ C`<sub>k</sub>*x <sub>k</sub>+ C`₀

a` <sub>11</sub> x <sub>1</sub> + a` ₁₂ x ₂ +...+ a` <sub>1k</sub>. x <sub>k</sub> ≤ a` ₁₀

a` <sub>21</sub> x <sub>1</sub> + a` ₂₂  x₂  +...+ a` <sub>2k</sub>  x <sub>k</sub>  ≤ a` ₂₀

......................................................................

a`<sub>m 1</sub> x <sub>1</sub>  + a` _{m 2} x₂ +...+ a` <sub>mk</sub> x <sub>k</sub>≤ a` _{m 0}

x j ≥ 0 , j = 1 k.

Пример выполнения работы

Перейти от канонической формы к однородной форме.

max Z = x₁ + x₂ + x₃+ x₄

(А)

1. В задаче два ограничения. Следовательно, m = 2. Выпишем все возможные группы из четырех переменных по две.

x₁ x₂; x₁ x₃; x₁ x₄; x₂ x₃; x₂ x₄; x₃ x₄

Найдем определители из коэффициентов при переменных этих групп:

x₁ x₂

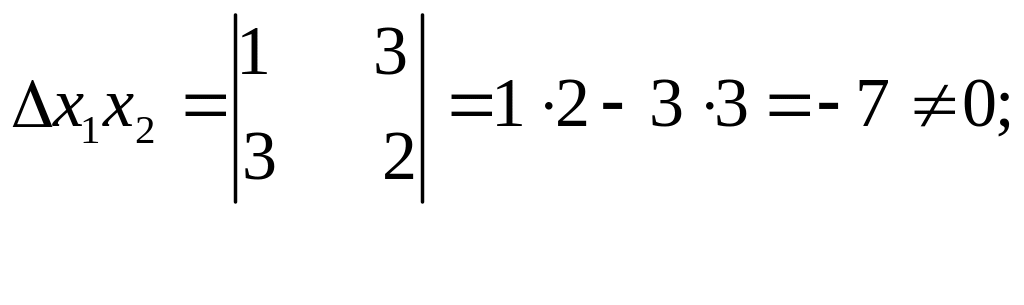
x₁ x₃

x₁ x₄

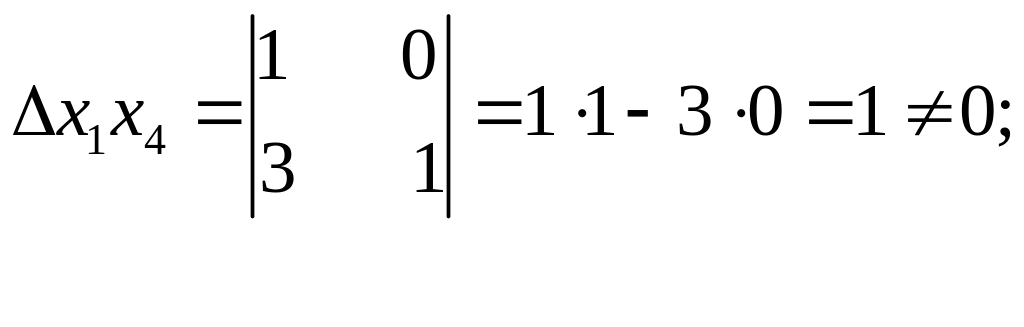
x₂ x₃

x₂ x₄

x₃ x₄

Для всех групп переменных определители отличны от нуля. Следовательно, данную систему можно привести к шести сочетаниям базисных переменных.

Перейдем к сочетанию базисных переменных х₁ х₂.

2. Перенесем в левую часть все элементы целевой функции. Получим

Z - x₁ - x₂ - x₃ - х₄ = 0.

3. Запишем систему ограничений и измененную целевую функцию в таблицу Гаусса. Получим таблицу 2.

Столбец контрольной суммы - это сумма всех элементов строки.

Таблица 2

Базисные переменные			Переменные
			Z	x1	x2		x3	x4	aio	kΣ
-			0	1	3		1	0	5	10
-			0	3	2		2	1	10	18	I*
Z			1	-1	-1		-1	-1	0	-3
			J*

4. Выполним первую итерацию преобразований Жордана - Гаусса.

За разрешающий элемент возьмем элемент во втором ограничении в столбце переменной x1. ai_*j_* = 3

Обведем его в рамку или в кружок, или выделим жирным шрифтом. Результаты расчетов запишем в таблице 3.

Разрешающую строку делим на разрешающий элемент:

a_2z^нов= =0; а₂₁^нов= = =1; а₂₂^нов= а₂₃^нов= ; а₂₄^нов= ;

а₂₀^нов= ; k .

В разрешающем столбце все элементы, кроме разрешающего элемента, равны нулю

a_1j* ^нов = 0; С₁ ^нов = a_3j* ^нов= 0.

Элемент, стоящий на месте разрешающего, равен единице a_i*j* ^нов = 1.

В разрешающей строке в столбце Z стоит 0, следовательно, столбец Z остается без изменений: a_iz ^нов = 0; a_3z ^нов = 1.

Проверим по правилу прямоугольника:

0	1	a1zнов= 0-
0	3

0	3	a1zнов= 1-
1	-1

Найдем элементы столбца x₂:

1	3	a12нов= 3-
3	2

3	2	C2нов=a32нов= -1-
-1	-1

Найдем элементы столбца x₃:

1	1	a13нов= 1-
3	2

3	2	C3нов=a33нов= -1-
-1	-1

Найдем элементы столбца x₄ :

1	0	a14нов= 0-
3	1

3	1	C4нов=a34нов= -1-
-1	-1

Найдем элементы столбца свободных членов:

1	5	a10нов= 5-
3	10

3	10	C0нов=a30нов=0-
-1	0

Найдем элементы столбца контрольных сумм:

1	10	kΣ1нов= 10-
3	18

3	18	kΣz нов= - 3 -
-1	-3

Контрольные суммы находятся для контроля вычислений. Сумма всех элементов строки должна совпадать с контрольной суммой, вычисленной по общим правилам преобразований Жордана - Гаусса.

В первой строке:

Во второй строке:

В третьей строке - строке целевой функции:

Все контрольные суммы совпали. Следовательно, вычисления выполнены верно и записаны в таблицу 3

Таблица 3

Базисные переменные

Переменные

Z

x1

x2

x3

x4

aio

kΣ

-

0

0

7/3

1/3

-1/3

5/3

4

i*

x1

0

1

2/3

2/3

1/3

10/3

6

Z

1

0

-1/3

-1/3

-2/3

10/3

3

J*

II. Перейдем ко второй итерации. Вторая строка уже была разрешающей. Третья строка - строка целевой функции, разрешающей быть не может, следовательно, разрешающей строкой может быть только первая строка.

Мы выбрали сочетание базисных переменных x₁,x₂ . Систему уже разрешили относительно x₁, следовательно, теперь ее разрешим относительно переменной x₂.

Разрешающий элемент

a _i*j* = .

Обведем его в рамку, в кружок или выделим жирным шрифтом.

Выполним преобразования Жордана - Гаусса и запишем результаты в таблицу 4.

Разрешающую строку делим на разрешающий элемент. В разрешающем столбце остальные элементы - нули. Запишем преобразования второй строки:

a₂₂ ^нов = 0; a₂₁ ^нов = 1,

т.к. в разрешающей строке в столбцах Z и x₁ стоят нули, то эти столбцы остаются без изменений.

a₂₃^нов =

a₂₄^нов =

a₂₀^нов =

kΣ₂ =

Найдем сумму элементов второй строки непосредственным сложением и сравним с kΣ₂ .

Суммы совпали. Преобразования выполнены верно.

Запишем преобразования третьей строки - строки целевой функции:

a_3Z^нов = 1; C₁^нов = 0,

т.к. в разрешающей строке в столбцах Z и x₁ стоят нули, то эти столбцы остаются без изменений.

C₂^нов = 0, как элемент разрешающего столбца.

C₃^нов =

C₄^нов =

C₀^нов =

KΣ^нов =

Проверим сумму элементов третьей строки непосредственным сложением и сравним с kΣ_Z .

1 -

В таблице 4 записаны полученные результаты:

Таблица 4

Базисные переменные	Переменные
	Z	x1	x2	x3	x4	aio	kΣ
x2	0	0	1	1/7	-1/7	5/7	12/7
x1	0	1	0	4/7	3/7	20/7	34/7
Z	1	0	0	-2/7	-5/7	25/7	25/7

Выполнили m =2 преобразований Жордана-Гаусса. Получили в базисе переменные x₂, x₁ .

Запишем систему, соответствующую таблице 4. Получим:

(A΄)

Система (А) эквивалентна системе (А'), так как выполняли эквивалентные преобразования.

Перенесем все члены целевой функции, кроме Z, в правую часть, получим целевую функцию

Z = 0·х₁ + 0·x₂+ ·х₃+ ·х₄ + 25/7.

Отбросим базисные переменные x₁, x₂, заменив тип ограничения равенства на неравенства типа меньше или равно и записав условия неотрицательности переменных, получим однородную форму задачи.

(A”)

max Z = ·х₃+ ·х₄ +

Системы А", А', A эквивалентны, так как получены в результате эквивалентных преобразований.

Перейдем теперь от заданной канонической формы к новому сочетанию базисных переменных, например, к сочетанию x₂,x₃. Мы уже проверили, что такое сочетание возможно.

Таблица 2’

	Базисные переменные		Переменные
		Z		x1	x2	x3	x4	aio	kΣ	i*
-		0		1	3	1	0	5	10
-		0		3	2	2	1	10	18
Z		1		-1	-1	-1	-1	0	-3
						J*

I итерация.

Возьмем разрешающей строкой первую строку, а разрешающим столбцом - столбец x₃. Тогда разрешающий элемент

a_i*j* = 1.

Обведем его в таблице 2' в рамку, в кружок или выделим жирным шрифтом.

Выполним первую итерацию преобразований Жордана-Гаусса. Результаты расчетов запишем в таблицу 3'.

II итерация.

Разрешающей строкой должна быть вторая строка. Мы выбрали сочетание базисных переменных x_2, x₃ . Систему уже разрешили относительно переменной x₃, следовательно, теперь ее разрешим относительно переменной x₂. Разрешающий элемент

a_i*j* = -4

Обведем его в рамку, в кружок или выделим жирным шрифтом.

Таблица 3'

Базисные переменные	Переменные
	Z	x1	x2	x3	x4	aio	kΣ
x3	0	1	3	1	0	5	10
-	0	1	-4	0	1	0	-2	i*
Z	1	0	2	0	-1	5	7
			j*

Выполним вторую итерацию Жордана - Гаусса. Результаты запишем в таблицу 4׳.

Таблица 4'

Базисные переменные	Переменные
	Z	x1	x2	x3	x4	aio	kΣ
x3	0	7/4	0	1	3/4	5	17/2
x2	0	-1/4	1	0	-1/4	0	1/2
Z	1	1/2	0	0	-1/2	5	6

Выполнили m = 2 преобразований Жордана - Гаусса. Получили в базисе переменные x₃ x₂. Запишем систему, соответствующую таблице 4', но предварительно перенесем все члены целевой функции, кроме Z, в правую часть. Получим

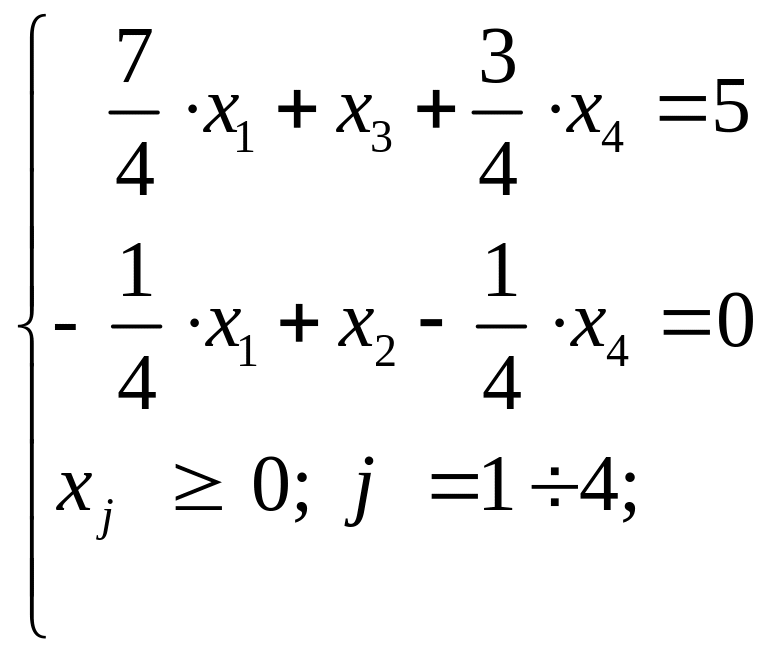(A״׳)

max Z = - ·х₁ + 0·x₂ + 0·х₃+ ·х₄ +5

Отбросив базисные переменные x₂ и x₃, заменив тип ограничения равенства на неравенства типа меньше или равно, записав условия неотрицательности переменных, получим однородную форму задачи

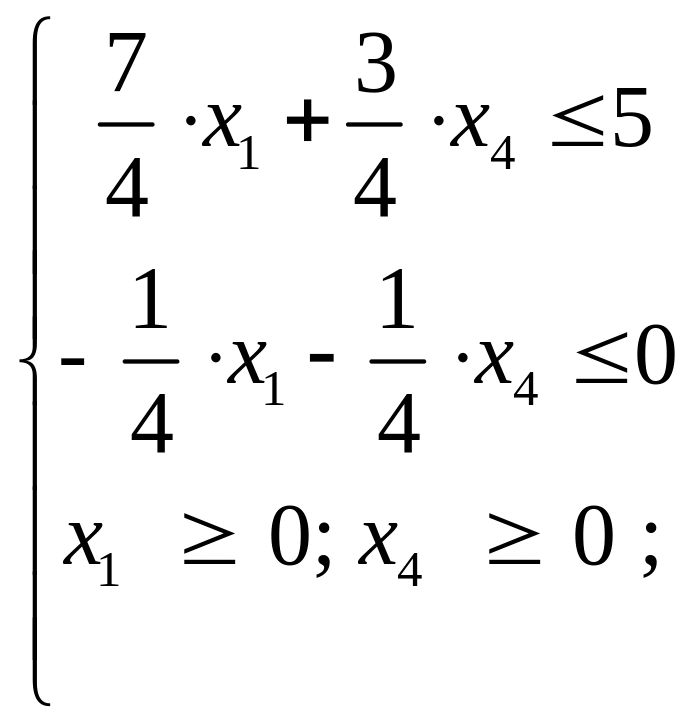(A^IY)

max Z = - х₁ + х₄ + 5.

Системы A ~ A^III ~ A^IV (системы эквивалентны), но A ~ A'~ A", то есть A ~ A'~ A" ~ A^III ~ A^IV.

Ранее мы показали, что данную систему можно привести к шести сочетаниям базисных переменных. При этом системы, полученные в результате перехода от канонической формы к однородной, эквивалентны между собой.

Список индивидуальных данных

Перейти от канонической формы задачи линейного программирования к однородной (значение k – меняется по указанию преподавателя).

Для этого:

- выявить возможные сочетания базисных переменных,

• выполнить в таблицах правила перехода для выбранного сочетания базисных переменных,

• записать эквивалентную каноническую форму найденного сочетания базисных переменных,

• записать эквивалентную однородную форму.

1. max Z = 5·x₁ + 3·x₂ + 4·x₃ + х₄

2. max Z = 3·x₁ + 4·x₂ + 5·x₃ + 2·х₄

3. max Z = 2·x₁ + 3·x₂ + 4·x₃ - 5·х₄

4. max Z = 3·x₁ + 5·x₂ - 6·x₃ + 7·х₄

5. max Z = 6·x₁ + 7·x₂ + 3·x₃ + 2·х₄

6. max Z = x₁ + x₂ + x₃ + х₄

7. max Z = 2·x₁ + 5·x₂ - 3·x₃ + 6·х₄

8. max Z = 3·x₁ + 2·x₂ + 6·x₃ + 4·х₄

9. max Z = 8·x₁ + 3·x₂ + 4·x₃ + 5·х₄

10. max Z = - x₁ + 3·x₂ + 4·x₃ - 2·х₄

11. max Z = -3·x₁ - 3·x₂ + x₃ + 5·х₄

12. max Z = 7·x₁ + 2·x₂ - 3·x₃ + 4·х₄

13. max Z = 2·x₁ - 3·x₂ + 4·x₃ + х₄

14. max Z = x₁ - 4·x₂ + 5·x₃ - 6·х₄

15. max Z = 4·x₁ + 2·x₂ + 6·x₃ + х₄

16. max Z = 2·x₁ - x₂ - 3·x₃ + 5·х₄

Выпишите свой пример:

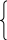max Z = x₁ x₂ x₃ х₄

x₁ x₂ x₃ х₄

x₁ x₂ x₃ х₄

x_j  0 j = 14

x₁ x₂; x₁ x₃; x₁ x₄;

x₂ x₃; x₂ x₄; x₃ x_4.

detx₁x₂

detx₁x₃

detx₁x₄

detx₂x₄

detx₂x₃

detx₃x₄

Каноническая форма

Однородная форма

Получите ещё новый базис, запишите для него каноническую и однородную форму:

Каноническая форма:

Однородная форма:

Получите ещё новый базис, запишите для него каноническую и однородную форму:

Каноническая форма:

Однородная форма:

Контрольные вопросы

1. Какие переменные называются:

• базисными;

• свободными?

2. Какое решение называется:

• возможным;

• общим;

• частным;

• допустимым;

• базисным;

3. Какая строка (ограничение) называется разрешающей?

4. Какой столбец (переменная)называется разрешающим?

5. Как найти разрешающий элемент?

6. Как в таблицах Гаусса преобразуется разрешающая строка?

7. Как в таблицах Гаусса преобразуется разрешающий столбец?

8. Как выполняются преобразования элементов таблицы по правилу прямоугольника?

9. Что образуют в таблице (системе) базисные переменные?

10. Какая переменная записывается в базис системы?

11. Какая форма записи задачи линейного программирования называется канонической?

12. Какая форма записи задачи линейного программирования называется однородной?