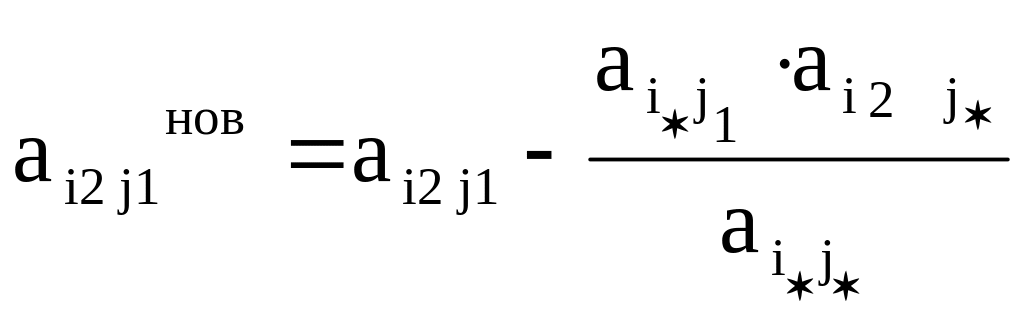Лабораторная работа № 2 «Переход от задачи в канонической форме к задаче в однородной форме»

Теоретическая часть

Переход от задачи в канонической форме к задаче в однородной форме

Возможны три случая перехода от канонической формы к однородной.

Приведём необходимые понятия и определения:

Рангом совместной системы линейных ограничений называется ранг её матрицы.

Чтобы решить задачу математического программирования (МП), необходимо найти совокупность значений n переменных, удовлетворяющую системе ограничений, условиям неотрицательности переменных и для которой целевая функция принимает наибольшее или наименьшее значение.

Возможным решением называется совокупность значений n переменных, удовлетворяющая системе ограничений задачи МП.

Д опустимым решением называется совокупность значений n переменных, удовлетворяющая системе ограничений и условиям неотрицательности.

Переменная, коэффициенты которой образуют единичный столбец

называется базисной.

Базисные переменные образуют единичный базис системы. Переменные, не входящие в единичный базис, называются свободными.

Решение называется общим, если базисные переменные выражены через свободные члены и свободные переменные:

x_i = a_io – a_{i, m+1}·x_m+1 – a_{i, m+2} · x_m+2- ... - a_i,n · x_n, i=1÷ m.

Решение называется частным, если в общем решении свободные переменные принимают любые значения.

Решение называется базисным, если система ограничений приведена к единичному базису, а все свободные переменные равны нулю.

I-й случай перехода от канонической формы к однородной

Каждое ограничение задачи в канонической форме содержит базисную переменную, причем в целевую функцию базисные переменные входят с нулевым коэффициентом. В этом случае, чтобы от задачи в канонической форме перейти к задаче в однородной форме, достаточно из ограничений, условий неотрицательности переменных и целевой функции отбросить базисные переменные, заменить ограничения равенства на ограничения типа меньше или равно.

Пример 1. Перейти от задачи в канонической форме к задаче в однородной форме.

max Z = 19∙x₁ + 17∙x₂ + 16∙x₃ + 0∙х₄ + 0∙х₅ +0∙х₆

Переменные х₄, х₅, х₆ - базисные, в целевой функции у этих переменных коэффициент 0, следовательно, эти переменные отбрасываем. Получаем

max Z = 19∙x₁ + 17∙x₂ + 16∙x₃

2-й случай

Каждое ограничение задачи в канонической форме содержит базисную переменную, но в целевую функцию базисные переменные входят с ненулевыми коэффициентами.

В этом случае, чтобы от задачи в канонической форме перейти к задаче в однородной форме, достаточно:

1) найти выражение базисных переменных через свободные члены и свободные переменные;

2) подставить выражение базисных переменных в целевую функцию;

3) в результате этих преобразований получится первый случай задачи в канонической форме;

4) выполнить преобразования 1-го случая перехода от задачи в канонической форме к задаче в однородной форме.

3-й случай

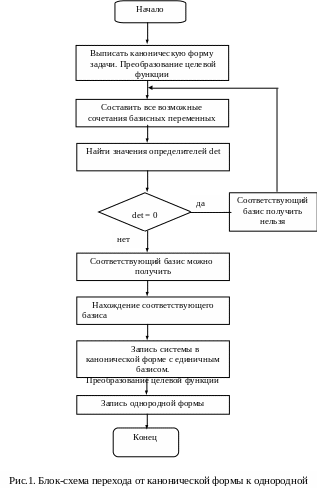
Каноническая форма не содержит в ограничениях базисных переменных. В этом случае для перехода к однородной форме необходимо (рис. 1):

1. Выделить группу из m переменных и найти значение определителя при этих m переменных. Если определитель равен нулю, то выделить новую группу переменных и найти значение определителя для новой группы переменных. И так до тех пор, пока не будет найдена группа переменных, для которой значение определителя отлично от нуля. Если значение определителя не равно нулю, то перейти к пункту 2.

2. Все элементы целевой функции, кроме свободного члена, перенести в левую часть: Z = С₁X₁ + С₂X₂ + ... + С_nX_n + С₀ ; Z - С₁X₁ - С₂X₂ - ... - С_nX_n = С₀.

3. Заполнить таблицу Гаусса следующего вида:

Таблица 1

Базисные переменные	Переменные
	Z	X1	X2	X3	...	Xn	aio	kΣ
-	0	a11	a12	a13	...	a1n	a10	kΣ1
-	0	a21	a22	a23	...	a2n	a20	kΣ2
.	.	.	.	.	...	.	.	.
-	0	am1	am2	am3	...	amn	am0	kΣm
Z	1	-C1	-C2	-C3	...	-Cn	Co	kΣz

Во второй строке таблицы перечислены переменные целевой функции и системы ограничений, свободный член a_io, контрольная сумма kΣ. В первом столбце таблицы - базисные переменные системы ограничений и целевой функции.

В третьей строке таблицы - коэффициенты при переменных первого ограничения, в четвёртой строке таблицы - коэффициенты при переменных второго ограничения и т.д., в (m+2)-й строке таблицы - коэффициенты m-го ограничения, в последней строке таблицы - коэффициенты целевой функции, полученные в пункте 2.

Столбец контрольной суммы kΣ- это сумма всех элементов строки, которую следует записывать в последний столбец таблицы.

4. Выполнить m преобразований Жордана-Гаусса (m итераций).

Переменная, относительно которой разрешается система, называется разрешающей и обозначается j*. Разрешающая переменная соответствует разрешающему столбцу.

Уравнение, которое разрешается относительно переменной, называется разрешающим и обозначается i*. Разрешающее уравнение соответствует разрешающей строке.

На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент, который обозначается a_i٭j٭.

а) Разрешающую переменную выбрать в столбце из группы m-переменных, определитель которой отличен от нуля и которая была выделена в первом пункте.

б) Разрешающая строка может быть любой, кроме строки целевой функции. Если эта строка была разрешающей ранее, то выбираем другую строку.

в) Разрешающий элемент должен быть отличен от нуля; если он равен нулю, то переходим к пункту 4а.

г) Все элементы разрешающей строки разделить на разрешающий элемент.

В столбец базисных переменных (первый) записать переменную разрешающего столбца.

д) Все элементы разрешающего столбца равны нулю

,

кроме элемента, стоящего на месте разрешающего. Элемент, стоящий на месте разрешающего, равен единице

е) Все остальные элементы таблицы считать по формуле

или по правилу прямоугольника.

Правило прямоугольника. Тот элемент, который заменяют, необходимо соединить диагональю с разрешающим элементом. На полученной диагонали построить прямоугольник. Провести вторую диагональ.

Из элемента, который заменяют, вычесть дробь, числителем которой является произведение элементов второй диагонали прямоугольника, а знаменателем разрешающий элемент (рис. 2).

Замечание. Если в разрешающей строке в каком-то столбце стоит ноль, то этот столбец останется без изменений.

Если в разрешающем столбце в какой-то строке стоит ноль, то эта строка останется без изменений.

5) Контроль вычислений. В последнем столбце таблицы записываются контрольные суммы, которые во всех таблицах, начиная со второй, считаются дважды:

• первый - выполняются по общим правилам преобразований Жордана - Гаусса;

• второй - непосредственным сложением всех элементов строки. Эти числа должны быть равными.

	j1		j ٭
i*	ai*j1		ai*j٭
i2	ai2j1		ai2j٭

	j1		j ٭
i1	ai1j1		ai1j٭
i*	ai*j1		ai*j٭

	j٭		j2
i*	ai*j٭		ai*j2
i2	ai2j٭		ai2j2

	j٭		j 2
i1	ai1j٭		ai1j2
i*	ai*j٭		ai*j2

Рис. 2. Вычисления по правилу прямоугольника

6) После m преобразований в каждой строке получаем базисную переменную, причем в целевую функцию эти базисные переменные входят с нулевым коэффициентом.

Выписать систему, соответствующую m+1 таблице. Перенести все члены целевой функции, кроме Z, в правую часть. Записать условия неотрицательности переменных.

7) Получаем систему, соответствующую первому случаю. Отбросив базисные переменные, можно получить однородную форму, записав вместо равенств неравенства типа меньше или равно (≤). Остается записать условия неотрицательности n-m переменных и вновь преобразованную целевую функцию.