Лабораторная работа № 6 «Получение исходного опорного решения»

Теоретическая часть

1 Общие сведения

Симплексный метод решения общей задачи линейного программирования основан на принципе последовательного улучшения опорного решения. Поэтому, чтобы его использовать, необходимо получить исходное опорное решение. Напомним, что решение называется опорным, если система ограничений приведена к единичному базису, свободные переменные равны нулю, а базисные переменные неотрицательные.

2 Переход от однородной формы или исходной формы общей задачи линейного программирования к канонической форме

а) с исходным опорным решением;

Пусть задача задана в однородной форме с неотрицательными свободными членами. При переходе к канонической форме в каждое ограничение неравенство типа меньше или равно (≤) вводится неотрицательная дополнительная переменная с коэффициентом плюс единица. Эти дополнительные переменные являются неотрицательными базисными, а основные переменные (переменные однородной формы) являются свободными переменными. Если свободные переменные приравнены нулю, то система приведена к исходному опорному решению.

б) с исходным базисным решением;

Пусть задача задана в однородной форме с произвольными свободными членами. При переходе к канонической форме дополнительные переменные станут базисными, как и в случае а), основные переменные являются свободными переменными, приравняем их к нулю. Полученное решение является базисным, так как оно удовлетворяет условиям: система приведена к единичному базису, свободные переменные равны нулю, а базисные переменные и неотрицательные, и отрицательные. Поэтому решение является только базисным, а не опорным. К такому базисному решению необходимо применить алгоритм получения исходного опорного решения, основанный на теореме о расширенном симплексном отношении (рассмотрим в пункте 3).

в) без единичного базиса;

Пусть задача задана в исходной форме, содержащей ограничения неравенства типа меньше или равно (≤), больше или равно (≥) и равно (=), неотрицательные свободные члены и неотрицательные переменные. Её сначала необходимо привести к канонической форме, введя дополнительные переменные в ограничения неравенства.

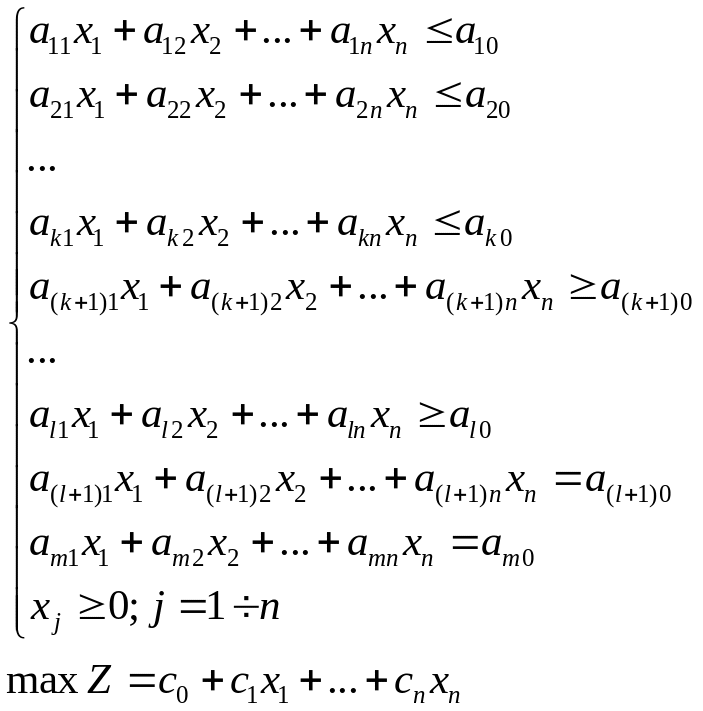
(1)

1. – исходная форма задачи, в которой m – ограничений, из них k - ограничений типа "≤", (l-k) – ограничений типа "≥", (m-l) – ограничений равенств, (k ≤ l ≤ m); n – переменных.

В этом случае каноническая форма задачи только в первых k – ограничениях будет содержать базисные переменные. Начиная с k+1 ограничения, каноническая форма не имеет базисных переменных. Следовательно, задача не приведена к единичному базису. Необходимо перейти к М-задаче всегда имеющей исходное опорное решение (рассмотрим это в пункте 4).

3 Переход от исходного базисного решения к исходному опорному решению

При переходе от исходного базисного решения к исходному опорному решению используют расширенные симплексные отношения. Расширенным симплексным отношением называется неотрицательное отношение свободных членов к ненулевым элементам разрешающего столбца.

а) Теорема. Если при преобразовании разрешающую строку выбрать по минимальному расширенному симплексному отношению, то после преобразования однократного замещения все неотрицательные свободные члены останутся неотрицательными.

б) Алгоритм получения исходного опорного решения.

1. Заполняется исходная таблица Гаусса с выделенным базисным решением, то есть с единичной подматрицей ( в каждом ограничении есть базисная переменная) и неположительными и положительными свободными членами.

1. Исходная таблица Гаусса

Баз\ пер

X1

X2



Xj*



Xk

Xk+1



Xi



Xk+m

a i0

К 

РСО0

Xk+1

a11

a12



a1j*



a1k

1



0



0

a10

К1

a10/ a1j*































Xi

ai1

ai2



aij*



aik

0



1



0

ai0

Кi

ai0/ aij*































Xk+m

am1

am2



amj*



am1

0



0



1

am0

Кm

am0/ amj*

2. По минимальному отрицательному свободному члену выбирается выделенная строка.

3. В выделенной строке по минимальному отрицательному коэффициенту при свободной переменной выбирается разрешающий столбец. Переход к пункту 4. Если такого коэффициента нет, то система ограничений не совместна в области допустимых (опорных) решений.

4. Находятся расширенные симплексные отношения (РСО).

5. По минимальному расширенному симплексному отношению выбирается разрешающая строка.

6. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент.

7. Разрешающий столбец определяет переменную, вводимую в базис.

8. Разрешающая строка определяет переменную, выводимую из базиса.

9. Выполняем пересчёт таблицы по правилам Жордана-Гаусса и заполняем новую таблицу. Если в новой таблице решение не является опорным, то переход к пункту 2.

Примечания.

1. Алгоритм позволяет за конечное число преобразований получить исходное опорное решение или выявить несовместность системы в области допустимых решений.

2. Если возникает неопределённость при выборе разрешающей строки, то есть минимальные расширенные симплексные отношения равны, то условимся за разрешающую строку брать строку с меньшим номером.

3. Если возникает неопределённость при выборе разрешающего столбца, то есть в выделенной строке несколько минимальных отрицательных коэффициентов при свободных переменных, то условимся за разрешающий столбец брать переменную с меньшим номером.