Лабораторная работа № 3 «Графический метод решения задач линейного программирования»

Теоретическая часть

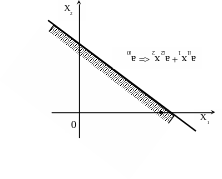
1 Геометрический смысл неравенства a_i1x₁ + a_i2x₂  a_i0

Заменим неравенство равенством a_i1x₁ + a_i2x₂ = a_i0 - это уравнение прямой, проходящей через две точки. Если a_i0  0, то

x1	0	ai0 / ai1
x2	ai0 / ai2	0

Н а координатной оси ОХ₁ откладываем точку (a_i0 / a_i1, 0), на оси ОХ₂ откладываем точку (0,a_i0 / a_i2) и соединяем эти точки прямой, которая называется граничной.

Если a_i0  0, то граничная прямая не проходит через начало координат. Подставляем координаты точки (0,0) в неравенство a_i1x₁ + a_i2x₂  a_i0 и проверяем: верное ли неравенство. Если a_i1* 0 + a_i2* 0 < a_i0 ,т.е. 0 < a_i0, то неравенство верное и полуплоскость с началом координат является искомой.

2 Область допустимых решений и допустимое решение

Областью допустимых решений является пересечение полуплоскостей системы ограничений и условий неотрицательности.

Условия неотрицательности переменных:

а) x₁  0 x₁ = 0 - ось ОХ₂; x₁  0 – полуплоскость справа от оси ОХ_2.

б) x₂  0 x₂ = 0 - ось ОХ₁; x₂  0 – полуплоскость сверху от оси ОХ_1.

Пересечением условий неотрицательности переменных x₁  0, x₂  0 является первая четверть координатной плоскости.

0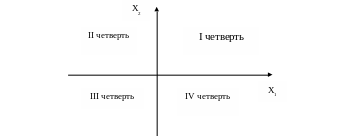

Решение является допустимым, если оно удовлетворяет системе ограничений и условиям неотрицательности переменных или если оно принадлежит области допустимых решений задачи.

Множество W называется выпуклым, если для любых двух несовпадающих точек найдется отрезок, соединяющий эти точки и целиком принадлежащий этому множеству.

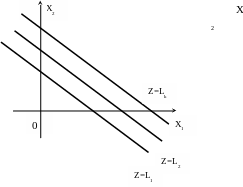
3 Линия уровня

Z = с₁x₁ + с₂x₂ + с₀ - линия уровня – прямая. Линий уровня бесчисленное множество, все они параллельны между собой.

Z = с₁x₁ + с₂x₂ + с₀ = const

_{Z = с1x1 + с2x2 + с0 = L}1

x1	0	(L1- с0 )/ с1
x2	(L1- с0 )/ с2	0

_{Z = с1x1 + с2x2 + с0 = L}2

x1	0	(L2- с0 )/ с1
x2	(L2- с0 )/ с2	0

. . .

_{Z = с1x1 + с2x2 + с0 = Lk}

x1	0	(Lk- с0 )/ с1
x2	(Lk- с0 )/ с2	0

4 Вектор – градиент

Вектор-градиент – частные производные Z по x₁ и x₂.

=

Z = с₁x₁ + с₂x₂ + с₀, = { с₁; с₂}. Строим точку (с₁; с₂) и соединяем начало координат с этой точкой. Получаем истинную длину вектора-градиента. Направление вектора-градиента от начала системы координат к точке (с₁; с₂).

Вектор-градиент показывает направление максимизации целевой функции.

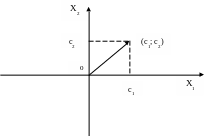
Вектор-градиент и линии уровня всегда взаимно перпендикулярны.