Контрольные вопросы

1. Какие переменные называются базисными, свободными?

2. Какое решение называется: базисным, опорным, допустимым?

3. Какое значение принимают свободные переменные в базисном решении?

4. Какое значение принимают свободные переменные в опорном решении?

5. Чему равны базисные переменные в базисном решении?

6. Чему равны базисные переменные в опорном решении?

7. Могут ли базисные переменные в базисном решении иметь отрицательное значение?

8. Могут ли базисные переменные в опорном решении иметь отрицательное значение?

9. Могут ли переменные в допустимом решении иметь отрицательное значение?

10. Какая строка является выделенной?

11. Как выбирается разрешающий столбец в выделенной строке?

12. Всегда ли М-задача имеет опорное решение?

13. В какие ограничения вводятся искусственные базисные переменные?

14. Вводятся ли искусственные базисные переменные в целевую функцию, если вводятся, то как?

15. Могут ли быть искусственные базисные переменные отрицательными?

16. Чему равны базисные переменные и искусственные базисные в опорном решении М задачи?

Лабораторная работа №7 - 12 «Решение общей задачи линейного программирования симплексным методом»

Теоретическая часть

Алгоритм симплексного метода в полных таблицах при решении задач на максимум целевой функции.

I этап схемы последовательного улучшения опорных решений.

1. Исходное опорное решение записывается в полную симплексную таблицу.

2. В первую строку симплексной таблицы записываются коэффициенты целевой функции при всех переменных, причем свободный член целевой функции записывается с противоположным знаком. В первый столбец записываются коэффициенты целевой функции при базисных переменных. Во второй столбец записываются базисные переменные, а во вторую строку – все переменные задачи, причем свободный член переносится в начало таблицы и обозначается а_i0.

3. Подсчитываются оценки по формуле оценок:

и записываются в последнюю строку таблицы.

№ таб.	cj	-c0	c1	c2	…	ci	…	cm	cm+1	…	cj*	…	cn	К∑ cj	co
ci	П Б	ai0	X1	X2	…	Xi	…	Xm	Xm+1	…	Xj*	…	Xn	К∑
c1	X1	a10	1	0	…	0	…	0	a1m+1	…	a1j*	…	a1n	∑1
c2	X2	a20	0	1	…	0	…	0	a2m+1	…	a2j*	…	a2n	∑2
…	…	…	…	…	…	…	…	…		…	…	…	…	…	…
ci	Xi	аi*0	0	0	…	1	…	0	aim+1	…	аi*j*	…	аi*n	∑i*
…	…	…	…	…	…	…	…	…		…	…	…	…	…	…
cm	Xm	am0	0	0	…	0	…	1	amm+1	…	amj*	…	amn	∑m
	∆j	Z=∆0	0	0	…	0	…	0	∆m+1	…	∆j*	…	∆n	∑∆j

II этап схемы последовательного улучшения опорных решений.

4. Проверка решения на оптимальность по признаку оптимальности: решение задачи на максимум целевой функции оптимально, если все оценки при переменных неотрицательные. Если критерий выполняется, то переход к п. 14(IV этап), если нет, то переход к п.5 (III этап).

III этап схемы последовательного улучшения опорных решений.

5. Разрешающий столбец выбирается по минимальной отрицательной оценке и обозначается j^*. Если наименьших отрицательных оценок несколько, то условимся выбирать разрешающий столбец по наименьшему номеру столбца с наименьшей отрицательной оценкой.

6. Если в разрешающем столбце есть хотя бы один положительный элемент, то переходим к п. 7, если нет, то целевая функция не ограничена.

7. Вычисляются симплексные отношения, то есть отношения неотрицательных свободных членов к строго положительным элементам разрешающего столбца и записываются в последний столбец.

8. По наименьшему симплексному отношению находится разрешающая строка и обозначается i^*. Если минимальных симплексных отношений несколько, то условимся выбирать разрешающую строку с меньшим номером среди минимальных симплексных отношений.

9. На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент, который обозначается .

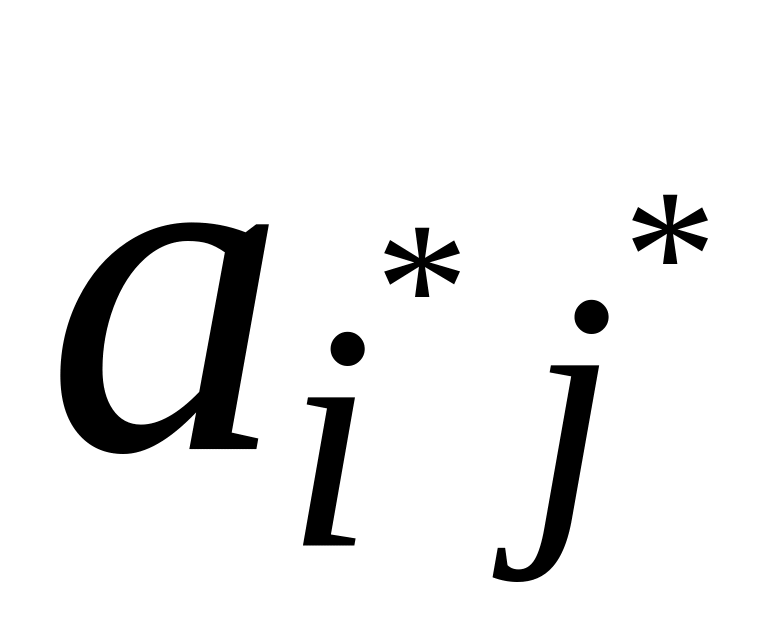10. Производится пересчет таблицы по правилу преобразования Жордана-Гаусса:

а) разрешающую строку делят на разрешающий элемент

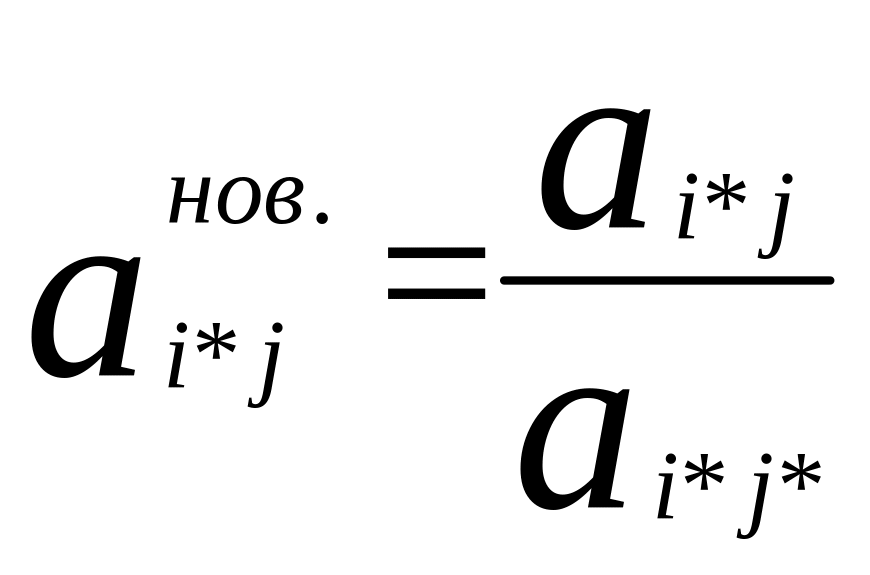
б) в разрешающем столбце элемент, стоящий на месте разрешающего равен единице, остальные элементы – нули

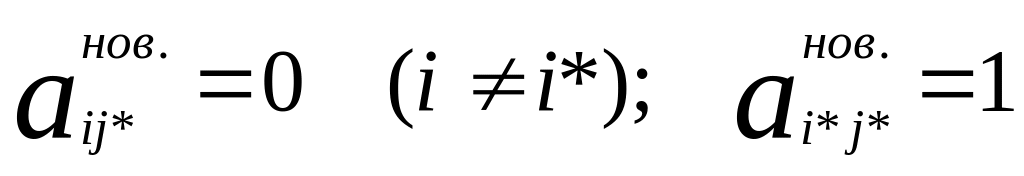
в) все остальные элементы таблицы, включая контрольную сумму и строку оценок, подсчитывают по правилу прямоугольника или по формуле

11. В разрешающей строке в столбец базисных переменных записывается переменная разрешающего столбца, а в столбец коэффициентов целевой функции при базисных переменных записывается коэффициент целевой функции разрешающего столбца.

12. Контроль вычислений осуществляется двумя способами:

а) по контрольным суммам, которые подсчитываются по общим правилам преобразований и непосредственно;

б) по оценкам, которые подсчитываются по формулам оценок (п.3) и по общим правилам преобразований.

Переход ко второму этапу схемы последовательного улучшения опорных решений.

13. Переход к пункту 4.

IV этап схемы последовательного улучшения опорных решений.

13. Запись оптимального решения и значения целевой функции.

Свободные переменные равны нулю. Значения базисных переменных равны соответствующим значениям в столбце свободных членов. Значение целевой функции равно ₀.

Примечание 1. Необходимо следить, чтобы свободные члены были неотрицательными. Если свободный член отрицательный, то разрешающая строка выбрана не по минимальному симплексному отношению.

Примечание 2. Симплексное отношение может быть равным нулю, а разрешающий элемент не может быть равным нулю, так как в симплексных таблицах он всегда положительный.

Пример выполнения работы

Задание 1.

Организация для производства двух видов продукции использует два вида производственных ресурсов: А, В.

Таблица 1. Расход ресурсов на единицу продукции и объём ресурсов

Вид ресурса	Расход ресурсов на единицу вида продукции, ед. веса		Всего ресурсов, ед. веса
	I	II
А	1	1	6
В	1	2.5	10
Стоимость единицы вида продукции, ден.ед.	2	5	-

Ресурсы могут быть недоиспользованы. Найти такое соотношение производства этих видов продукции, которое обеспечит максимальный объем производства продукции в стоимостном выражении.

I) Запишем условия задачи в математическом виде в исходной (однородной) форме.

Обозначения:

Переменные.

Х₁, ед. - количество продукции 1-го вида,

Х₂, ед. - количество продукции 2-го вида.

Целевая функция.

Z,ден.ед. - максимальный объём продукции.

Запишем условия задачи в математическом виде.

Составим ограничения.

1. Баланс ресурсов вида А, ед.

X₁ + X₂ ≤ 6

[ед.] = [ед.]

2. Баланс ресурсов вида В, ед. веса

X₁ + 2,5X₂ ≤ 10

3. Условия неотрицательности переменных.

X₁ ≥ 0, X₂ ≥ 0

Целевая функция: max Z = 2X₁ + 5X₂

Перейдём к канонической форме задачи.

1. X₁ + X₂ +X₃= 6,

где X₃, ед. - недоиспользование ресурсов вида А,

2. X₁ + 2,5X₂ +X₄=10,

где X₄, ед. - недоиспользование ресурсов вида В.

3. Условия неотрицательности переменных.

X_j ≥ 0, j=1÷ 4

Целевая функция: max Z = 2X₁ + 5X₂ +0X₃+0X_4.

А. Каноническую форму задачи с исходным опорным решением X(0;0;6;10),так как задача приведена к единичному базису (X₃,X₄) с неотрицательными значениями базисных переменных,

1. X₁ + X₂ +X₃= 6,

2. X₁ + 2,5X₂ +X₄=10,

3. X_j ≥ 0, j=1÷ 4

max Z = 2X₁ + 5X₂ +0X₃+0X₄

запишем в симплексную таблицу.

№1	Cj	-C0=0	C1=2	C2=5	C3=0	C4=0	7	С.О.
Ci	Баз.\пер.	аi0	X1	X2	X3	X4	kΣ	ai0≥0/ aij*>0
0	X3	6	1	1	1	0	9	6:1=6
0	X4	10	1	2,5	0	1	14,5	10:2,5=4	I*
Z	∆j	0	-2	-5	0	0	-7	х
				J*

В первой строке симплексной таблицы (С.Т.)записаны коэффициенты целевой функции, причем C₀ с противоположным знаком. В первом столбце С.Т.- коэффициенты целевой функции при базисных переменных. В последней строке С.Т. записываются оценки, подсчитанные по формуле оценок.

.

Б. ∆₀= 0*6+0*10- 0=0; ∆₁=0*1+0*1-2=-2; ∆₂=0*1+0*1-5=-5; ∆₃=j₄= 0*1+0*0-0=0.

В. Проверяем решение на оптимальность. Решение не оптимально, так как не все оценки при переменных не отрицательны. ∆₁< 0, ∆₂< 0.

Г. По минимальной отрицательной оценке выбираем разрешающий столбец. Это столбец X₂, так как -5<-2.

Д. Находим по минимальному симплексному отношению разрешающую строку, на пересечении разрешающей строки и разрешающего столбца определяем разрешающий элемент, с которым выполняем преобразования однократного замещения. Получаем новую таблицу. Далее по алгоритму.

Задание 2.

Пусть требуется определить оптимальное сочетание трех культур - пшеницы, ячменя и картофеля. Имеются следующие производственные ресурсы: посевная площадь - 700 га, труда - 33600 человеко-часов и денежных средств на сумму 1000000 денежных единиц. Причем в связи с потребностью в зерне посевная площадь под зерновыми культурами должна быть не менее 350 га.

Таблица 1а. Затраты труда, средств на 1га и выход продукции с 1 га культур

Показатель	Культура
	Пшеница	Ячмень	Картофель
Затраты труда на 1 га, чел-ч	40	24	240
Затраты материально-денежных средств, ден.ед.	150	150	500
Выход валовой продукции с 1 га, денежные единицы	325	350	1000

Критерий оптимальности задачи - максимум валовой продукции в стоимостном выражении. Производственные ресурсы могут быть недоиспользованы, если это целесообразно с точки зрения критерия оптимальности.

Введем обозначения в задаче:

Переменные:

х₁, га - искомая посевная площадь под пшеницей;

х₂, га - искомая посевная площадь под ячменем;

х₃, га - искомая посевная площадь под картофелем;

Z - целевая функция - максимум валовой продукции в стоимостном выражении, денежные единицы.

Составляем по условию задачи систему ограничений.

Первое ограничение соответствует условию по использованию и наличию пашни.

1. Баланс площади посевов, га

х₁ + х₂ + х₃ ≤ 700.

Проверим единицы измерения левой и правой частей ограничения - это гектары, они совпадают. Поэтому ограничение записано верно.

Второе ограничение соответствует условию по использованию трудовых ресурсов.

40 чел-ч затрачивают на 1 га пшеницы, поэтому на всю посевную площадь пшеницы затрачивают 40∙х₁ (чел-ч), аналогично, на 1 га ячменя затрачивают 24 чел-ч, а на всю площадь под ячменем затрачивают 24∙х₂ (чел-ч), на 1 га картофеля используют 240 чел-ч, на весь картофель 240∙x₃ (чел-ч). Всего в наличии 33600 чел-ч, поэтому можем записать ограничение.

2. Баланс трудовых ресурсов, чел-ч

4 0∙х₁ + 24∙х₂ + 240∙х₃ ≤ 33600

Проверим единицы измерения обеих частей ограничения:

Они совпадают.

Третье ограничение соответствует условию по использованию и наличию материально-денежных средств.

Рассуждения по записи третьего ограничения совпадают с рассуждениями по записи второго ограничения.

3. Баланс материально-денежных средств, денежные единицы

150∙х₁ + 150∙х₂ + 500∙х₃ ≤ 1000000

(ден.ед./га)*га = ден.ед.

Четвертое ограничение по использованию площади пашни по посевам зерновых культур.

4. Площадь под зерновыми культурами не менее 350 га

х₁ + х₂ ≥350.

[га] = [га]

5. Условия неотрицательности переменных:

x₁≥0; x₂ ≥0; x₃≥0

Целевая функция задачи записывается в виде следующего математического выражения:

max Z = 325∙x₁ + 350∙x₂+ 1000∙x₃

ден.ед. = (ден.ед./га)*га.

Рассуждения по записи целевой функции аналогичны рассуждениям по записи второго ограничения, так как в целевой функции коэффициенты при переменных определяют выход валовой продукции с 1 га культуры в стоимостном выражении.

Получили следующую запись условий задачи в исходной форме:

max Z = 325∙x₁ + 350∙x₂ + 1000∙x₃ .

Перейдем к канонической форме записи задачи.

В исходной форме все переменные неотрицательные, ограничений равенств нет, поэтому вводим неотрицательные дополнительные переменные и заменяем ограничения неравенства на ограничения равенства.

Первое ограничение - неравенство типа меньше либо равно, поэтому вводим с коэффициентом плюс единица дополнительную переменную х₄, так как основных переменных в задаче три (n = 3), получаем

х₁ + х₂ + х₃+ х₄ = 700 , где х₄, га означает недоиспользование посевной площади.

Второе ограничение - неравенство типа " ≤ ", поэтому введем с коэффициентом "+1" новую дополнительную переменную х₅, получаем

40∙х₁ + 24∙х₂+ 240∙х₃+ х₅ = 33600,

где х_{5 ,} чел-ч означает недоиспользование трудовых ресурсов.

Третье ограничение - неравенство типа " ≤ " поэтому вводим новую дополнительную переменную х₆ с коэффициентом плюс единица.

Получаем 150∙х₁+ 150∙х₂ + 500∙х₃+ х₆ = 1000000,

где х₆, денежные единицы, означает недоиспользование материально-денежных средств.

Четвертое ограничение - типа больше или равно, поэтому вводим новую дополнительную переменную х₇ с коэффициентом "-1", получаем

х₁ + х₂ - х₇ = 350,

где х₇, га означает использование посевной площади под зерновыми культурами сверх минимальной границы 350 га.

Пятое: условия неотрицательности всех семи переменных.

Так как дополнительные переменные показывают лишь степень выполнения того или иного условия задачи, не являются основными переменными задачи, то они не влияют на значение целевой функции, поэтому в целевую функцию они вводятся с нулевыми коэффициентами.

Получаем, max Z = 325∙x₁ + 350∙x₂ + 1000∙x₃+ 0∙х₄+ 0∙х₅ + 0∙х₆ + 0∙х₇

Канонической формой задачи является следующая запись:

max Z = 325∙x₁ + 350∙x₂ + 1000∙x₃ + 0∙х₄+ 0∙х₅ + 0∙х₆ + 0∙х₇

Экономический смысл дополнительных переменных:

х₄, га означает недоиспользование посевной площади.

х_{5 ,} чел-ч означает недоиспользование трудовых ресурсов.

х₆, денежные единицы, означает недоиспользование материально-денежных средств.

х₇, га означает использование посевной площади под зерновыми культурами сверх минимальной границы 350 га.

Задача приведена к канонической форме с неотрицательными свободными членами, но не содержащей единичного базиса (X₄, X₅,X₆ - базисные переменные, а X₇ - свободная переменная), поэтому её надо сначала специальными методами привести к исходному опорному решению, и только потом применять симплексный метод.

Список индивидуальных данных

Ввести обозначение переменных, целевой функции с единицами измерений. Записать условия задачи в математическом виде в исходной форме: названия ограничений с единицами измерений, ограничения, проверка единиц измерения, целевая функция, проверка единиц измерений. Перейти и записать каноническую форму задачи с экономическим значением дополнительных переменных. Проверить: есть ли единичный базис в канонической форме и приведена ли задача к исходному опорному решению. Решить симплексным методом. Сделать вывод о полученном решении, записать ответ в виде вектора решения и выписать значения целевой функции и переменных с экономическим содержанием.

1. Возделываются следующие культуры: горох, овес и кормовая свекла. Площадь посевов - 500 га, трудовые ресурсы - 33600 чел-ч, материально-денежные средства (МДС) - 100000 денежных единиц. Посевная площадь кормовой свеклы не более 50 га.

Таблица 2. Затраты труда, средств на 1 га и выход валовой продукции с 1 га культур

Культура	Затраты на 1 га		Выход валовой продукции с 1 га, ден. ед.
	труда, чел.-час	материально-денежных средств, ден. ед.
Горох	33,6	100	250
Овес	24	100	300
Кормовая свекла	336	250	800

Найти оптимальное сочетание посевов сельскохозяйственных культур, обеспечивающее максимум производства валовой продукции в стоимостном выражении.

2. В отделении возделываются культуры - многолетние и однолетние травы на зеленый корм и на сено. Площадь пашни - 400 га, трудовые ресурсы - 16000 чел-ч, площадь многолетних трав на зеленый корм - не более 100 га.

Таблица 3. Затраты труда на 1 га и выход кормов с 1 га

Показатели	Многолетние травы		Однолетние травы
	на зеленый корм	на сено	на зеленый корм	на сено
Затраты труда на 1 га, чел.-ч	16,0	24,0	32,0	40,0
Выход кормов с 1га, ц к.ед.	30,0	25,0	25,0	20,0

Критерий оптимальности - максимум производства кормов со всей площади.

3. Возделываются культуры: овес, озимая пшеница, картофель. Посевная площадь - 700 га, посевная площадь озимых зерновых – не более 1/3 от площади всех зерновых, посевная площадь картофеля - не более 200 га.

Таблица 4. Урожайность и цены реализации продукции

Культура	Урожайность, ц/га	Цена реализации, ден. ед./ц
Овес	20,0	9
Озимая пшеница	25,0	13
Картофель	150,0	6

Найти оптимальное сочетание посевов сельскохозяйственных культур, обеспечивающее максимум производства валовой продукции в стоимостном выражении.

4. Возделываются три культуры: овес, кукуруза на силос, многолетние травы на сено.

Площадь пашни - 600 га, трудовые ресурсы - 24000 чел.-час. Посевная площадь овса не должна превышать 200 га. Соотношение посевных площадей кукурузы на силос и многолетних трав следующее: площадь под кукурузой не более 1/2 общей площади пашни под этими культурами.

Таблица 5. Затраты труда на 1 га и выход кормов с 1 га

Культура	Выход кормов с 1 га, ц к.ед.	Затраты труда на 1 га, чел.- час.
Овес	25,0	24,0
Кукуруза на силос	24,0	16,0
Многолетние травы на сено	16,0	16,0

Найти оптимальное сочетание посевов этих культур, обеспечивающее наибольшее производство кормов в ц к.ед.

5. Возделываются картофель (его площадь не более 250 га), ячмень, горох. Посевная площадь - 1000 га, объем минеральных удобрений – 850 ц д.в.

Таблица 6. Нормы внесения удобрений, урожайность и цены реализации продукции

Культура	Нормы внесения минеральных удобрений на 1 га, ц д.в.	Урожайность, ц/га	Цены реализации, ден. ед./ц
Картофель	3,0	100	6
Ячмень	1,0	20	9
Горох	2,0	15	20

Найти оптимальное сочетание посевов сельскохозяйственных культур, обеспечивающее максимум производства валовой продукции в стоимостном выражении.

6. Две культуры: кормовая свекла и кукуруза на силос могут возделываться или без орошения, или с поливом. Площадь орошаемой пашни - 200 га, площадь богарных (неполивных) земель - 600 га. Ресурсы труда - 96000 чел.-ч, ресурсы воды - 1500000 м³.

Таблица 7. Нормы затрат ресурсов и выход кормов

Показатель	Кормовая свекла		Кукуруза на силос
	на поливе	без полива	на поливе	без полива
Затраты труда, чел.-ч/га	400	160	240	160
Норма полива, тыс. м3/га	1,0	-	2,0	-
Выход кормов с 1 га, ц к. ед.	50,0	30,0	60,0	22,0

Найти оптимальное сочетание посевов сельскохозяйственных культур, обеспечивающее максимальное производство кормов в кормовых единицах.

7. Для производства кукурузы и гороха на зерно выделено 1200 га посевных площадей, 48000 чел-час трудовых ресурсов и 2500 тракторо-смен.

Таблица 8. Затраты ресурсов на 1 ц и цена реализации 1 ц

Показатель	Затраты на 1 ц
	кукурузы	гороха
Пашня, га	0,025	0,05
Трудовые ресурсы, чел.-ч	1,8	0,32
Трудовые ресурсы механизаторов, тракторо-смен	0,064	0,37
Цена реализации 1 ц, ден. ед.	5,5	10

Найти оптимальное сочетание посевов сельскохозяйственных культур, обеспечивающее максимум валовой продукции в стоимостном выражении.

8. В отчете о прибылях и убытках при методе учёта полных затрат рассчитывается валовая прибыль, как разность между выручкой от реализации продукции и производственной себестоимостью реализованной продукции.

Найти оптимальное сочетание посевов сельскохозяйственных культур, обеспечивающее максимум валовой прибыли при производстве и реализации трех видов продукции.

Имеются ресурсы: посевная площадь в объёме 800 га, трудовые ресурсы в объёме 4400 чел.-дней, материально-денежные средства в объёме 100000 денежных единиц.

Экономические показатели даны в таблице 9.

Таблица 9. Экономические показатели

Вид продукции	Урожайность, ц/га	Затраты на 1 га		Выручка от реализации 1 ц продукции, ден.ед.	Себестоимость 1 ц произведенной продукции, ден.ед.	Конечные остатки 1 ц произведенной продукции, ден.ед.
		труда, чел.-дн.	материально-денеж-ных средств, ден.ед.
1	2	3	4	5	6	7
1	28	5	100	53,9	21,8	2,3
2	30	4	150	28,6	16,1	1,2
3	26	8	50	20.3	14,2	3,4

Пояснение. Обозначим выручку от реализации 1 ц продукции j-ого вида V_j ,ден.ед., себестоимость 1 ц произведенной продукции j-ого вида C_j ,ден.ед., конечные остатки 1 ц произведенной продукции j-ого вида K_j,ден.ед., валовую прибыль от реализации 1 ц продукции j-ого вида WP_j,ден.ед. Тогда формула расчета валовой прибыли от реализации 1 ц продукции j-ого вида имеет вид: WP_j = V_j – (C_j - K_j ), где (C_j - K_j ) – производственная себестоимость реализованной продукции. После расчета валовой прибыли от реализации 1 ц продукции j-ого вида её величину надо умножить на урожайность продукции j-ого вида, получим валовую прибыль от реализации продукции j-ого вида с одного гектара. Эти величины можно записать в таблицу 9, добавив новый столбец.

9. В отчете о прибылях и убытках при методе учёта полных затрат рассчитывается операционная прибыль (до налогообложения), как разность между валовой прибылью от реализации продукции и суммой коммерческих и административных расходов на реализацию продукции.

Используя условия задачи 8, определить операционную прибыль каждого вида продукции и максимум операционной прибыли (до налогообложения) всей продукции, если известны переменные и постоянные коммерческие расходы, административные расходы на каждый вид продукции.

Таблица 10. Исходные данные

Вид продукции	Валовая прибыль от реализации 1 ц продукции, ден.ед.	Коммерческие расходы на реализацию 1 ц продукции, ден. ед.		Административные расходы на реализацию 1 ц продукции, ден.ед.	Сумма коммерческих (переменных и постоянных) расходов на реализацию 1 ц продукции, ден.ед.	Сумма коммерческих и административных расходов на реализацию 1 ц продукции, ден.ед.	Операционная прибыль (до налогообложения) от реализации 1 ц продукции, ден.ед.
		переменные	постоянные
1	2	3	4	5	6	7	8
1		10,5	4,8	8,2
2		2,2	2,3	1,5
3		0,7	0,3	2,0

Пояснение. Обозначим коммерческие переменные расходы на реализацию 1 ц продукции j-ого вида KM1_j ,ден.ед., коммерческие постоянные расходы на реализацию 1 ц продукции j-ого вида KM2_j ,ден.ед., сумму коммерческих (переменных и постоянных) расходов на реализацию 1 ц продукции j-ого вида KMR_j, ден.ед., административные расходы на реализацию 1 ц продукции j-ого вида A_j, ден.ед. , cумму коммерческих и административных расходов на реализацию 1 ц продукции j-ого вида KMAR_j,ден.ед. Тогда формула расчета операционной прибыли (до налогообложения) 1 ц продукции j-ого вида OP_j,ден.ед. имеет вид: OP_j= WP_j – KMAR_j,ден.ед , где KMAR_j = KMR_j + A_j ,ден.ед, а KMR_j= KM1_j,+ KM2_j, ден.ед.

Задание 2. Составить по образцу условия семи задач линейного программирования, имеющих разные варианты решения, и решить их симплексным методом.

Образец.

1. 3х1+2х26 2х1+3х26 х1 ≥ 0, х2 ≥ 0 maxZ=5х1+3х2+6	5. -3х1-2х2-6 -2х1-3х2-6 х1 ≥ 0, х2 ≥ 0 maxZ=-3х1-2х2+6
2. 3х1+2х26 2х1+3х26 х1 ≥ 0, х2 ≥ 0 maxZ=3х1+2х2+6	6. - 3х1+2х26 - 2х1+3х26 х1 ≥ 0, х2 ≥ 0 maxZ=-3х1- 4х2+6
3. 3х1-2х26 2х1-3х26 х1 ≥ 0, х2 ≥ 0 maxZ=-3х1+2х2+6	7. х1+х23 -х1-х2-6 х1 ≥ 0, х2 ≥ 0 maxZ=3х1+2х2+6
4. 3х1+2х26 - х1-2х2-6 х1 ≥ 0, х2 ≥ 0 maxZ=3х1+2х2+6

Задание 3. Получить у преподавателя индивидуальный вариант задачи. Ввести обозначения переменных, целевой функции с единицами измерений. Записать условия задачи в математическом виде в исходной форме: названия ограничений с единицами измерений, ограничения, проверка единиц измерения, целевая функция, проверка единиц измерений. Перейти и записать каноническую форму задачи с экономическим значением дополнительных переменных. Проверить: есть ли единичный базис в канонической форме и приведена ли задача к исходному опорному решению. Решить симплексным методом. Сделать вывод о полученном решении, записать ответ в виде вектора решения и выписать значения целевой функции и переменных с экономическим содержанием.

Задача. Организация для производства двух видов продукции использует два вида производственных ресурсов: А, В.

Таблица 11.

Вид ресурса	Расход ресурсов на единицу вида продукции, ед.*		Всего ресурсов, ед.
	1	2
А	а11	а12	а10
В	а21	а22	а20
Стоимость единицы вида продукции, ден.ед.	С1	С2	-

*) Если коэффициент при какой-либо переменной отрицательный, то предполагается, что соответствующий ресурс в данном процессе производится, а не расходуется.

Ресурсы могут быть недоиспользованы. Найти такое соотношение производства этих видов продукции, которое обеспечит максимальный объем производства продукции в стоимостном выражении.

Задачу линейного программирования: 1) записать в однородной (исходной) форме (правила записи смотрите в лабораторной работе 1).

2). Решить графическим методом. Записать ответ с экономическим содержанием

3). Решить на основе фундаментальной теоремы, то есть перейти от однородной формы к канонической, преобразовать целевую функцию, записать исходное опорное решение с преобразованной целевой функцией в таблицу Гаусса, выполнить симплексные преобразования однократного замещения, выписать опорное решение и значение целевой функции, найти оптимальное решение среди всех опорных решений, сравнив значения целевых функций и выбрав среди них максимальное. Каждому опорному решению поставить в соответствие вершину области допустимых решений, полученную графическим методом.

4) Решить симплексным методом. Записать решение из последней симплексной таблицы.

Вариант	а11	а12	а10	а21	а22	а20	С1	С2	С0
1	1	2	3	1	1	1	1	2	4
2	2	4	8	2	2	4	2	1	3
3	-1	1	2	1	2	10	1	3	5
4	1	2	3	2	1	3	1	1	2
5	-2	3	6	3	-2	12	4	3	1
6	3	4	12	3	-4	8	2	5	4
7	1	2	4	2	-2	6	3	1	4
8	2	-1	6	1	4	4	1	1	5
9	1	4	8	1	2	4	1	6	3
10	2	1	4	1	2	4	1	1	-2
11	1	1	4	2	1	2	1	2	1
12	2	1	6	1	1	4	1	2	4
13	1	1	5	-1	1	3	2	4	1
14	-1	1	2	2	1	8	1	-3	3
15	2	1	5	2	-3	6	3	6	1
16	1	-1	2	2	1	6	1	1	-3
17	7	2	7	4	-2	2	1	2	2
18	-1	2	2	1	1	4	1	3	5
19	1	1	4	2	-1	3	1	1	-3
20	2	1	4	3	2	6	1	5	2
21	1	-1	2	2	3	9	2	1	-1
22	3	-4	6	1	2	4	2	3	-2
23	2	3	6	2	1	2	1	3	4
24	2	3	6	1	2	2	2	1	6
25	3	1	6	1	1	4	2	1	5
26	2	3	6	1	2	4	1	1	3
27	1	1	2	2	1	1	1	2	1
28	1	-1	1	2	1	4	1	1	-2
29	1	1	10	3	-1	5	1	4	9
30	2	5	10	2	1	6	3	-1	3
31	2	3	6	3	2	6	1	2	-3

Контрольные вопросы

1. На каком принципе построен симплексный метод?

2. Как рассчитываются оценки в С.Т.?

3. Как определяют оптимально ли решение при поиске максимума целевой функции?

4. Как находят разрешающий столбец в С.Т.?

5. Как находят разрешающую строку в С.Т.?

6. Всегда ли однозначно определяется разрешающая строка в С.Т.?

7. Всегда ли однозначно определяется разрешающий столбец в С.Т.?

8. Из чего состоит задача математического программирования?

9. Что называется целевой функцией задачи математического программирования?

10. Что называется ограничением задачи математического программирования?

11. Как вводятся дополнительные переменные в ограничения типа меньше либо равно?

12. Как вводятся дополнительные переменные в ограничения типа больше либо равно?

13. Как вводятся дополнительные переменные в ограничения типа равно?

14. Как вводятся дополнительные переменные в целевую функцию?

15. Какой экономический смысл дополнительных переменных, введенных в ограничения типа меньше либо равно?

16. Какой экономический смысл дополнительных переменных, введенных в ограничения типа больше либо равно?

17. Чему равны дополнительные переменные, введенные в ограничения типа меньше либо равно?

18. Чему равны дополнительные переменные, введенные в ограничения типа больше либо равно?