4 Получение исходного опорного решения м-задачи.

В задаче, записанной в канонической форме с неотрицательными свободными членами, но не имеющей в каждом ограничении базисную переменную, для получения исходного опорного решения разрешающую строку можно выбирать по минимальному симплексному отношению, то есть отношению неотрицательных свободных членов к строго положительным элементам разрешающего столбца, причём разрешающий столбец выбирается произвольно среди столбцов свободных переменных. При больших размерностях задачи эти преобразования громоздки, поэтому к таким задачам применяют правила перехода к М-задаче, всегда имеющей исходное опорное решение.

Правила перехода к м-задаче от исходной формы (основной) задачи

1. В ограничения типа меньше или равно (≤) вводим неотрицательные дополнительные переменные с коэффициентом плюс единица.

2. В ограничения типа больше или равно (≥) вводим неотрицательные дополнительные переменные с коэффициентом минус единица.

3. В ограничения, не содержащие базисные переменные, вводим неотрицательные искусственные базисные переменные Y_i.

4. В целевую функцию дополнительные переменные вводятся с нулевым коэффициентом.

5. В целевую функцию искусственные базисные переменные Y_i при решении задачи на максимум целевой функции вводятся с коэффициентом "-М", а при решении задачи на минимум целевой функции вводятся с коэффициентом "+М", где "М" большое положительное число: М ≥ 10⁴.

Правила перехода к М-задаче от канонической формы (основной) задачи без единичного базиса с неотрицательными свободными членами

1. В ограничения, не содержащие базисные переменные, вводим неотрицательные искусственные базисные переменные Y_i.

2. В целевую функцию искусственные базисные переменные Y_i при решении задачи на максимум целевой функции вводятся с коэффициентом "-М", а при решении задачи на минимум целевой функции вводятся с коэффициентом "+М", где "М" большое положительное число: М ≥ 10⁴.

Таким образом, получаем следующую М-задачу:

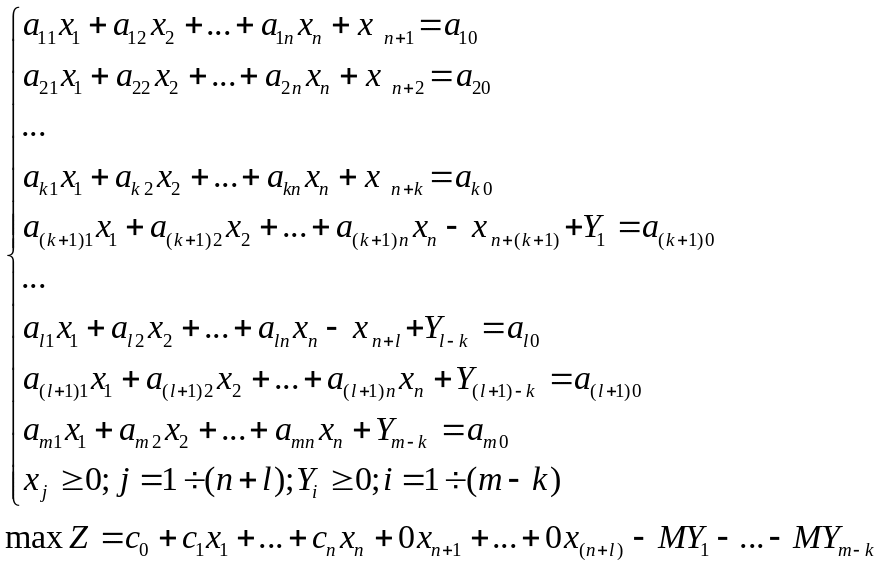
Задача приведена к единичному базису. Каждое ограничение имеет базисные переменные. Это соответственно: X_n+1, X_n+2,..., X_n+k, Y₁, ... , Y _m-k . Свободным переменным присвоим значение ноль, тогда базисные переменные равны неотрицательным свободным членам. Задача имеет следующее опорное решение

X(0,0, ... , 0, a₁₀, a₂₀, ... , a_k0, 0, ... , 0, a_(k+1)0, ... , a_l0, a_(l+1)0, ... , a_m0).

Значение целевой функции для исходного опорного решения М-задачи имеет вид: Z= C₀ -Ma_(k+1)0- ... -Ma_l0-Ma_(l+1)0- ...-Ma_m0.

Пример выполнения работы:

Получить исходное опорное решение в примерах 1-3.

Пример 1.

5X₁+3X₂-X₃ 10

6X₁-5X₂+2X₃  15

X₁0, X₂0, X₃0

maxZ=4X₁+3X₂+2X₃

Перейдём к канонической форме, получим

5X₁+3X₂-X₃ +X₄= 10

6X₁-5X₂+2X₃ +X₅=15

X_j0, j=15

maxZ=4X₁+3X₂+2X₃+0X₄+0X₅

Переменные X₄ и X₅ - базисные переменные, X₁, X₂ и X₃ - свободные переменные, равные нулю, поэтому задача приведена к исходному опорному решению.

Исходное опорное решение имеет вид X_{исх.опорное}(0,0,0,10,15).

Пример2. 3X₁+2X₂ 6

X₁-X₂  -9 .

-X₁-2X₂  -4

X_j0, j=12

maxZ=4X₁+3X₂

Перейдём к канонической форме.

3X₁+2X₂+X₃ = 6

X₁-X₂ +X₄= -9 - выделенная строка.

-X₁-2X₂ +X₅= -4

X_j0, j=15

maxZ=4X₁+3X₂+0X₃+0X₄+0X₅

Получили каноническую форму, каждое ограничение которой содержит базисную переменную, то есть система приведена к единичному базису, но свободные члены произвольные (и положительные, и отрицательные числа). Поэтому система приведена к исходному базисному решению X_{исх.базисное}(0,0,6,-9,-4). В выделенной строке есть отрицательный коэффициент при свободной переменной, поэтому исходное базисное решение записываем в таблицу Гаусса.

Баз\ пер	X1	X2	X3	X4	X5	a i0	РСО
X3	3	2	1	0	0	6	6/2=3
X4	1	-1	0	1	0	-9	-9/ (-1)=9	выдел.строка
X5	-1	-2	0	0	1	-4	-4/ (-2)=2	I
		j

Баз\ пер	X1	X2	X3	X4	X5	a i0	РСО
X3	2	0	1	0	1	2	2/1=2	I
X4	3/2	0	0	1	-1/2	-7	-7/ (-1/2)=14	выдел.строка
X2	1/2	1	0	0	-1/2	2	-
					j

Баз\ пер	X1	X2	X3	X4	X5	a i0	РСО
X5	2	0	1	0	1	2	-
X4	5/2	0	1/2	1	0	-6	-	выдел.строка
X2	3/2	1	1/2	0	0	3	-

Выделенная строка с минимальным отрицательным свободным членом «-6». В выделенной строке нет ни одного отрицательного коэффициента при переменных, следовательно, система не совместна в области опорных (допустимых) решений. Можно это проверить графическим методом.

Пример 3. X₁+2X₂ 8

-3X₁-2X₂  -6 .

-X₁+0,5X₂ -3

X_j0, j=12

maxZ=X₁+6X₂

Перейдём к канонической форме.

X₁+2X₂+X₃ = 8

-3X₁-2X₂ +X₄= -6 - выделенная строка.

-X₁-0,5X₂ +X₅= -3

X_j0, j=15

maxZ=X₁+6X₂+0X₃+0X₄+0X₅

Получили каноническую форму, каждое ограничение которой содержит базисную переменную, то есть система приведена к единичному базису, но свободные члены произвольные (и положительные, и отрицательные числа). Поэтому система приведена к исходному базисному решению X_{исх.базисное}(0,0,8,-6,-3). В выделенной строке есть отрицательные коэффициенты при свободных переменных, поэтому исходное базисное решение записываем в таблицу Гаусса.

Баз\ пер	X1	X2	X3	X4	X5	a i0	РСО
X3	1	2	1	0	0	8	8/1=4
X4	-3	-2	0	1	0	-6	-6/ (-3)=2	выдел.строка I
X5	-1	0,5	0	0	1	-3	-3/ (-1)=3
	j

Баз\ пер	X1	X2	X3	X4	X5	a i0	РСО
X3	0	4/.3	1	1/3	0	6	6/(1/3)=18
X1	1	2/3	0	-1/3	0	2	-
X5	0	7/6	0	-1/3	1	-1	-1/(-1/3)=3	выдел.строка I
				j

Баз\ пер	X1	X2	X3	X4	X5	a i0	РСО
X3	0	5/2	1	0	1	5	-
X1	1	-1/2	0	0	-1	3	-
X4	0	-7/2	0	1	-3	3	-

Система приведена к единичному базису, все свободные члены неотрицательные, следовательно, система совместна в области опорных (допустимых) решений. Получили исходное опорное решение X(3,0,5,3,0), в котором свободные переменные X₂ и X₅ равны нулю, а базисные переменные неотрицательные. Можно это проверить графическим методом, найдя на графике вершину с координатами (3, 0), однозначно соответствующую исходному опорному решению.

Пример 3а.

Получить исходное опорное решение М задачи.

X₁+2X₂ 8

-3X₁-2X₂  -6 .

-X₁+0,5X₂ -3

X_j0, j=12

maxZ=X₁+6X₂

Задача дана в однородной форме, но не все свободные члены неотрицательные. Приведём задачу к исходной форме с неотрицательными свободными членами.

X₁+2X₂ 8

-3X₁+2X₂  6 .

X₁-0,5X₂ 3

X_j0, j=12

maxZ=X₁+6X₂

Перейдём к записи задачи в канонической форме. Получим

X₁+2X₂+X₃ = 8 , X₃ - базисная переменная;

3X₁+2X₂ -X₄ = 6 .

X₁-0,5X₂ -X₅= 3

X_j0, j=15

maxZ=X₁+6X₂+0X₃+0X₄+0X₅

Получили каноническую форму, но не каждое ограничение её содержит базисную переменную, то есть система не приведена к единичному базису, причём свободные члены неотрицательные числа. Поэтому систему приведем к исходному опорному решению М задачи, введя во второе и третье ограничения искусственные неотрицательные базисные переменные Y_i. Получим

X₁+2X₂+X₃ = 8 , X₃ - базисная переменная;

3X₁+2X₂ -X₄ +Y₁ = 6, Y₁ - искусственная базисная переменная;

X₁-0,5X₂ -X₅ +Y₂= 3 , Y₂ - искусственная базисная переменная;

X_j0, j=15

maxZ=X₁+6X₂+0X₃+0X₄+0X₅ -M*Y₁ –M*Y₂

Система приведена к единичному базису с неотрицательными свободными членами. Пусть свободные переменные равны нулю, тогда исходное опорное решение М задачи имеет вид Хисходн. опорное решение М задачи(0,0,8,0,0,6,3),

Z(Хисходное опорное решение М задачи)= -M*6 –M*3= - 9М. Оно не совпадает с исходным опорным решением основной задачи.

Список индивидуальных данных

1). Получить исходное опорное решение с помощью расширенных симплексных отношений или установить несовместность системы ограничений в области допустимых (опорных) решений.

2). Получить исходное опорное решение М задачи и подсчитать Z(X_{исх.опор}._{М задачи}).

3) Проверить результат графическим методом.

Z=C₁*X₁+C₂*X₂+C₀

a_i1* Х₁+ a_i2*Х₂(   a_i0, I=1m

Х₁  0, Х₂  0

№ вари- анта	Х1	Х2	Тип ограничения			№ варианта	Х1	Х2	Тип ограничения
	ai1	ai2	  	ai0			ai1	ai2	  	ai0
1						2
maxZ	-1	-2		-3		minZ	1	2		5
	1	1		4			-1	1		4
	2	1		2			2	-1		2
	1	2		2			-1	2		2
3						4
maxZ	-1	-2		4		minZ	1	1		6
	1	1		7			1	1		7
	2	1		2			-2	1		2
	1	2		2			1	-2		2
5						6
minZ	3	1		2		maxZ	1	2		4
	1	1		3			1	1		5
	2	-3		6			-1	1		3
	3	–2		6			1	-1		3
7						8
maxZ	-1	2		-5		maxZ	1	-3		-9
	1	1		5			1	1		6
	2	-1		6			2	-1		4
	-1	2		6			-1	2		4
9						10
maxZ	2	-4		3		minZ	-2	-2		3
	5	2		10			2	5		10
	2	-1		4			2	-3		6
	-1	2		4			-3	2		6
11						12
maxZ	3	6		7		minZ	-3	-3		-7
	3	1		6			3	1		6
	2	-1		10			2	-1		5
	-1	2		10			-1	2		5
13						14
maxZ	-3	4		7		minZ	-4	2		-7
	-1	-2		-6			-1	-1		-4
	2	-3		-6			2	1		2
	1	-2		2			1	2		2
15						16
minZ	-3	1		2		maxZ	1	-2		4
	1	1		-3			1	1		-5
	2	-3		6			-1	1		3
	3	–2		12			1	-1		8
17						18
maxZ	-1	2		-5		maxZ	-1	-3		9
	1	1		5			1	1		6
	2	-1		6			2	-1		4
	-1	2		6			-1	2		4
19						20
maxZ	2	5		3		minZ	-5	-2		-3
	5	2		10			2	5		10
	2	-1		-4			2	-3		6
	-1	2		14			-3	2		-6
21						22
maxZ	3	-4		8		minZ	-3	4		-8
	3	1		6			3	1		6
	2	-1		1			2	-1		15
	-1	2		1			-1	2		15
23						24
maxZ	-1	2		7		minZ	-8	2		-7
	-1	-2		6			-1	1		-4
	2	-3		-6			2	-1		-2
	3	-2		12			1	-2		2
25						26
minZ	3	-1		12		maxZ	-1	2		14
	1	1		3			1	1		6
	2	-3		12			-1	1		3
	3	–2		6			1	-1		3
27						28
maxZ	1	-2		-5		maxZ	-1	-3		9
	1	1		5			1	1		6
	2	-1		6			-2	-1		4
	-1	-2		6			-1	-2		4
29						30
maxZ	2	3		3		minZ	-2	-3		-3
	5	2		10			2	5		10
	-2	-1		4			-2	-3		6
	-1	-2		4			-3	-2		6
31						32
maxZ	3	5		7		minZ	-5	-2		-7
	3	1		6			3	1		6
	-2	-1		10			-2	-1		5
	-1	-2		10			-1	-2		5
33						34
maxZ	-3	-2		2		minZ	3	2		-6
	-1	-2		-6			-1	-1		-4
	-2	-3		6			2	1		2
	-1	-2		2			-1	-2		2