Билет № 8

1. Медный кубик (Е = 1.110⁵ МПа,  = 0.35) с ребром а = 100 мм вложен без зазоров в гнездо стальной плиты, деформациями которой можно пренебречь. Вычислить деформации сторон кубика и проверить его прочность.

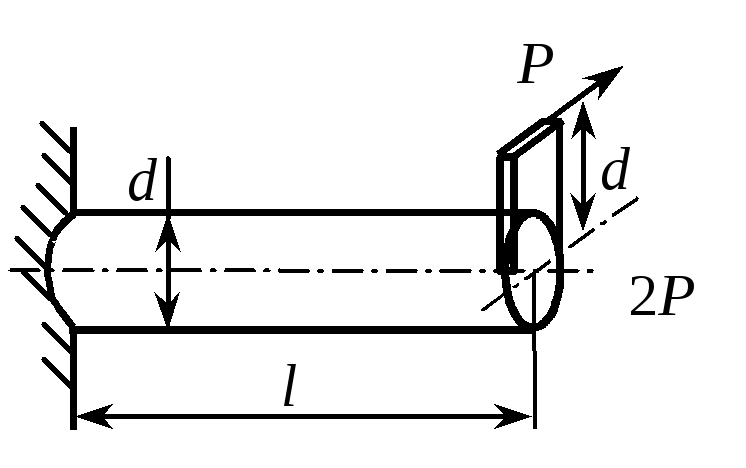
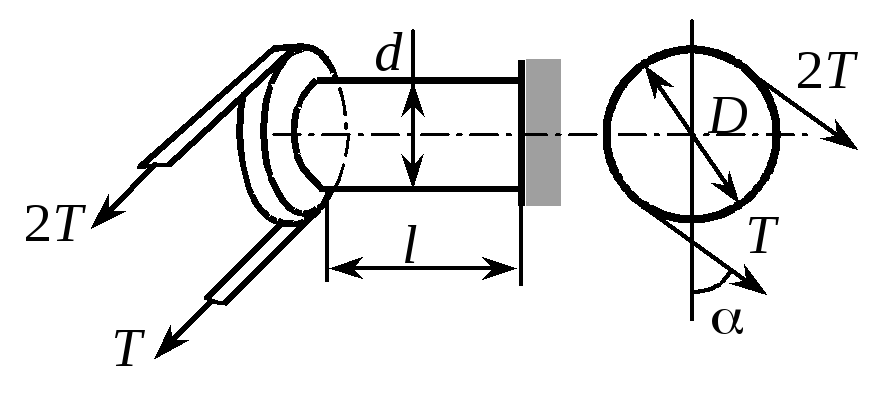
2. Используя III-ю теорию прочности, найти эквивалентное напряжение. Показать точку, в которой оно действует. Р = 20 кН, d = 10 см, l = 1 м.

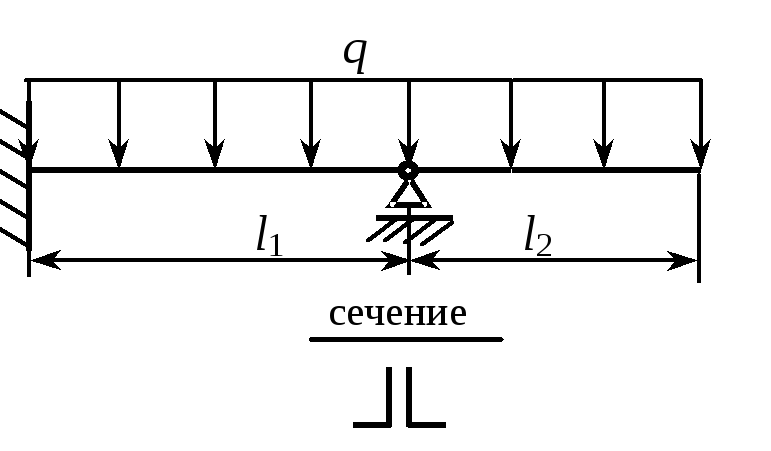
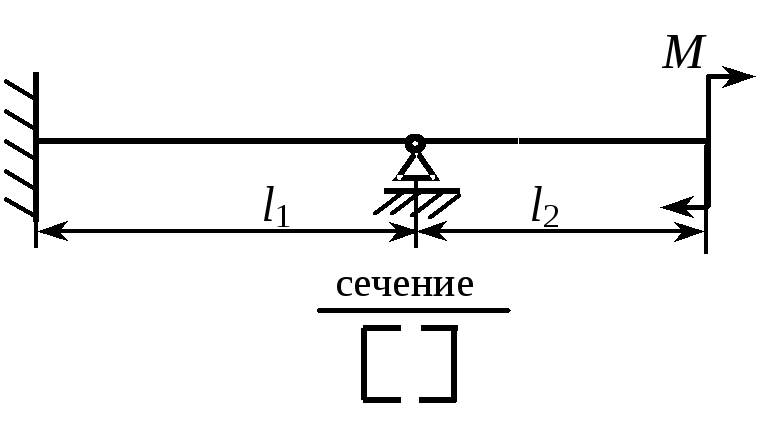
3. Из условия прочности подобрать сечение балки из стали 3 (_Т = 240 МПа), если q = 15 кН/м, l₁ = 3 м, l₂ = 1 м.

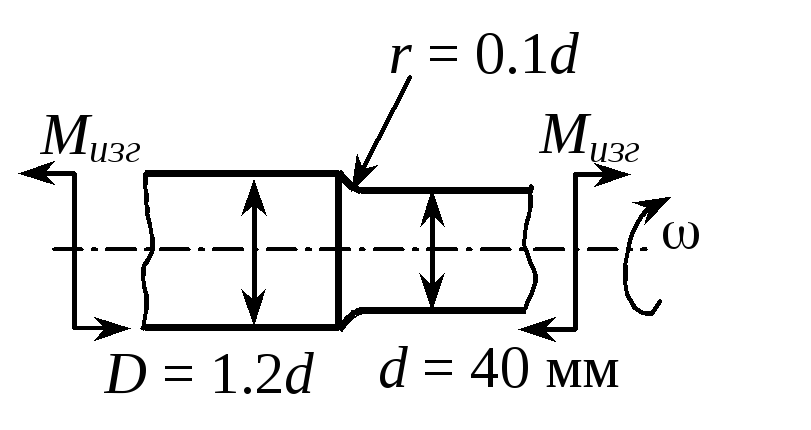
4. Вал редуктора диаметром d = 40 мм из стали 40Х (_в = 900 МПа, _-1 = 400 МПа) спроектирован на действие постоянного изгибающего момента М_изг = 6 кНм. Как изменится запас его усталостной прочности, если его поверхность подвергнуть цементации?

5. Грузоподъемность домкрата, имеющего винт из Ст. 5 (Е = 2.110⁵ МПа, _Т = 250 МПа) с внутренним диаметром d = 20 мм и длиной l = 0.5 м, равна N_кр. Как изменится эта величина, если длину домкрата увеличить до l = 0.8 м?

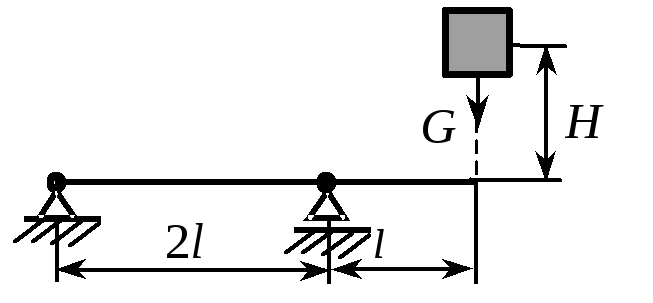
6. На стальную балку прямоугольного сечения bh = 4060 мм (l = 1 м) высоты H = 40 мм падает груз весом g = 1 кН. Определить динамические реакции, возникающие в опорах балки. Как они изменятся, если груз приложить мгновенно без начальной скорости?

1. Стальной кубик (Е = 2.010⁵ МПа,  = 0.25) с ребром а = 50 мм и медный (Е = 1.010⁵ МПа,  = 0.36) с ребром 2а поочередно сжимаются на прессе. Определить величину соотношения между сжимающими их усилиями N₁ и N₂, вызывающими одинаковые упругие укорочения.

2. Используя III-ю теорию прочности, найти эквивалентное напряжение. Показать точку, в которой оно действует. Т = 20 кН, d = 2d = 16 см, l = 1 м,  = 60.

3. Из условия прочности подобрать сечение балки из стали 3 (_Т = 240 МПа), если М = 10 кНм, l₁ = 2 м, l₂ = 2 м.

4. Определить запас прочности стержня из стали 40ХН (_в = 900 МПа, _-1 = 400 МПа, _-1 = 240 МПа) диаметром D = 60 мм с поперечным отверстием 5 мм, нагружаемого переменным крутящим моментом, меняющимся от - 2кНм до 8 кНм.

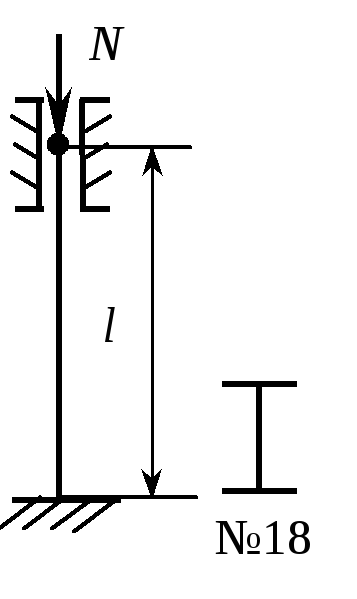
5. Стальной стержень (Е = 2.010⁵ МПа, [] = 200 МПа) двутаврового сечения длиной l = 6 м сжимается силой N. Исходя из условий прочности и устойчивости определить грузоподъемность стержня.

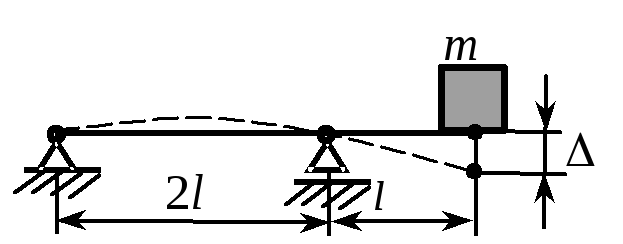
6. На балке лежит груз массой m, под действием которого она прогибается на  = 1.5 см. Как изменится этот прогиб, если тот же груз упадет с высоты H = 0.75 м?