Свойства последовательно соединённых элементов

Рассмотрим пример электрической цепи, приведенный на рисунке 3.14, состоящей из разнородных элементов (четырех резистивных элементов - , , , , трех индуктивностей - , , и двух емкостей - , ), соединенных последовательно.

Вычертим векторную диаграмму этой цепи (рис. 3.15).

Вектор тока откладываем в произвольном направлении. Далее откладываем падение напряжения на всех элементах: напряжения и ток на резистивных элементах совпадают по фазе, напряжение на индуктивных элементах по фазе опережает ток на , ток на емкостных элементах опережает напряжение на .

Используя векторную диаграмму можно определить величину напряжения на любом участке электрической цепи и его сдвиг по фазе относительно тока. Например, напряжение между точками схемы 3 и 8 равно - , а между точками 6 и 9 - .

В общем случае суммарное падение напряжения на резистивных элементах равно , на индуктивных элементах - , на емкостных элементах - . Таким образом, последовательно соединённые резистивные, индуктивные и емкостные можно заменить эквивалентными. Они соответственно равны:

.

Тогда полное сопротивление всей ветви, соответственно равно:

При последовательном соединении резистивного, индуктивного и емкостного элементов, напряжение на зажимах цепи, можно разбить на две составляющие напряжения активную и реактивную (рис. 3.16).

Из приведенной векторной диаграммы следует: , .

Пример 3.1. Возможные варианты расчета цепей с последовательным соединением, рассмотрим на примере электрической цепи, представленной на рисунке 3.17. Заданы величины U = 170 (B), ω = 314 (рад/с) (f = 50 Гц), r₁ = 10 (Ом), r₂ = 9 (Ом), r₃ = 14 (Ом), L₁ = 30 (мГн), С₂ = 90 (мкФ), L₃ = 25 (мГн). Необходимо определить ток в цепи, напряжения на элементах цепи и напряжение на участке 3-6.

1. Определяем омические сопротивления реактивных элементов:

(Ом),

(Ом),

(Ом).

2. Определяем полное сопротивление ветви.

   1. Эквивалентное активное сопротивление

(Ом).

2. Эквивалентное индуктивное сопротивление

(Ом).

3. Эквивалентное емкостное сопротивление

(Ом).

2.4. Полное сопротивление

(Ом).

3. Определяем ток в цепи 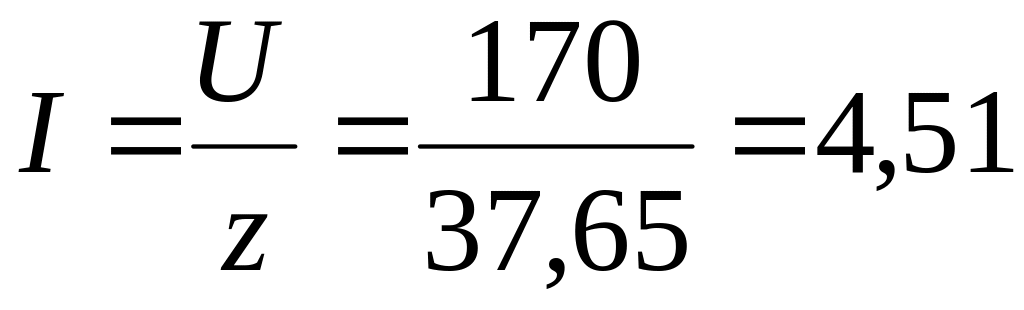(А).

4. Определяем напряжения на каждом элементе цепи

(В),

(В),

(В),

(В),

(В),

(В).

5. Напряжение на участке цепи 3-6 равно

(В).

6. Векторная диаграмма рассматриваемой цепи приведена на рисун- ке 3.18.

3.5. Параллельное соединение r, l, c

На рисунке 3.19. приведена электрическая схема с параллельно соединенными элементами r, L, C и к цепи приложено напряжение

Проводимости каждой ветви соответственно равны:

.

Эти формулы имеют ограниченное применение, т.е. они справедливы в том случае, если ветвь содержит один идеальный элемент.

Согласно первому закону Кирхгофа общий ток равен:

.

Оценку соотношений между действующими значениями токов в каждой ветви электрической цепи можно оценить с помощью векторной диаграммы, изображенной на рисунке 3.20.

Порядок построения векторной диаграммы следующий.

1. Откладываем вектор напряжения в произвольном направлении.

2. Далее откладываем токи в каждой из параллельных ветвей:

   1. Ток на резистивном элементе совпадает по направлению с напряжением .

   2. Ток на индуктивном элементе отстает по направлению от напряжения на 90⁰.

   3. Ток на емкостном элементе опережает по направлению напряжение на 90⁰.

3. Результирующий вектор тока , получаем путем векторного сложения , , (начало вектора соединяем с концом вектора ).

На приведенной векторной диаграмме ток опережает напряжение на угол , следовательно, режим работы активно-емкостной.

Из векторной диаграммы следует:

,

где – полная проводимость цепи.

Выражение I =Uу представляет закон Ома для цепи синусоидального тока.

Соотношения между величинами активной , реактивной и полной проводимостями можно оценить с помощью треугольника проводимостей (рис. 3.21).

Из этого треугольника следует:

.

Цепь с произвольным числом параллельно соединенных идеальных элементов, по аналогии, обладает следующими свойствами. Однородные параллельно соединенные элементы можно заменить эквивалентными и тогда:

g =  g_i ;

b_L =  b_Li ;

b_C =  b_Ci .

Таким образом, параллельно соединённые одноименные сопротивления можно заменить эквивалентными.

В общем случае, при параллельном соединении резистивного, индуктивного и емкостного элементов, ток в неразветвленном участке цепи, можно разбить на две составляющие тока активную и реактивную (рис. 3.22).

Из векторной диаграммы следует: .

Пример 3.2. Возможные варианты расчета цепей с параллельным соединением, рассмотрим на примере электрической цепи, представленной на рисунке 3.23. Заданы величины U = 150 (B), ω = 314 (рад/с) (f = 50 Гц), r₁ = 22 (Ом), r₂ = 17 (Ом), r₃ = 14 (Ом), L₁ = 60 (мГн), С₂ = 300 (мкФ), L₃ = 30 (мГн). Необходимо определить токи в ветвях I_i и ток в неразветвленном участке цепи I.

1. Определяем омические сопротивления реактивных элементов:

(Ом),

(Ом),

(Ом).

2. Определяем полную проводимость цепи.

1. Проводимость ветвей с резистивными элементами

(См),

(См),

(См).

Эквивалентная проводимость ветвей с резистивными элементами

(См).

2. Проводимости ветвей с индуктивными элементами

(См),

(См).

Эквивалентная проводимость ветвей с индуктивными элементами

(См).

3. Проводимость ветви с емкостным элементом

(См).

Эквивалентная проводимость ветвей с емкостным элементом

(См).

2.4. Полная проводимость

(См).

3. Определяем ток в цепи (А).

4. Определяем токи в каждой параллельной ветви

(А),

(А),

(А),

(А),

(А),

(А).

7. Векторная диаграмма рассматриваемой цепи приведена на рисунке 3.24.