Рассмотрим практическое применение этого положения

Пусть имеются два синусоидальных тока и с одинаковой частотой и различными амплитудами и начальными фазами:

,

.

Допустим необходимо получить сумму этих токов .

Подобные операции сложения токов синусоидальных величин используются в первом законе Кирхгофа.

В результате сложения этих токов (рис. 3.5), получим синусоидальный ток такой же частоты, но со своей амплитудой и начальной фазой:

.

Так как частота этих токов одинакова, то они вращаются с одинаковой частотой ω. Т.е. эти вектора друг относительно друга неподвижны, то для определения I_m можно применить операцию векторного сложения. В результате такого сложения мы получим величины I_m и _i, а следовательно все характеристики мгновенного значения результирующего тока i.

Из примера следует, что законы Кирхгофа для действующих (максимальных) значений цепей синусоидального тока выполняются в векторной форме. Графическое изображение действующих значений токов (напряжений) в электрических схемах называют векторной диаграммой токов (напряжений) цепи.

3.3. Протекание синусоидального тока по r, l, c

1. Синусоидальный ток в цепи с резистивным элементом

Пусть имеется резистивный элемент r (рис. 3.6), по которому протекает синусоидальный ток .

Согласно закону Ома на этом элементе возникает падение напряжения:

.

Максимальные значения тока и напряжения связаны выражением:

.

Следовательно, действующие значения тока и напряжения также связаны выражением: .

Из вышеизложенного следует, что напряжения и ток на резистивном элементе совпадают по фазе, т. е. имеет место совпадение максимальных значений в один момент времени. Это означает, что векторы действующих значений тока и напряжения направлены в одну сторону.

На рисунке 3.7,а показаны кривые мгновенных значений тока и напряжения на резистивном элементе, на рисунке 3.7,б – векторная диаграмма токов и напряжения.

Мгновенная мощность определяется как .

Среднее значение мощности за период равно:

.

Резистивный элемент называется активным сопротивлением, т.к. протекание синусоидального тока сопровождается потреблением активной мощности.

2. Синусоидальный ток в цепи с индуктивным элементом

Пусть имеется индуктивный элемент L (рис. 3.8), по которому протекает синусоидальный ток равный .

На зажимах возникает напряжение , которое согласно закону Фарадея равно: .

Из выражения u_L следует, что максимальное значение напряжения и ток индуктивности связаны выражением:

,

где имеет размерность сопротивления и называется индуктивным сопротивлением.

Следовательно, действующие значения тока и напряжения связаны выражением: .

Напряжение по фазе опережает ток на и вектор напряжения опережает ток на 90.

На рисунке 3.8,а показаны кривые мгновенных значений тока и напряжения на индуктивном элементе, на рисунке 3.8,б – векторная диаграмма токов и напряжения.

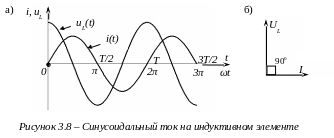
При положительных значениях напряжений, в интервале , напряжение имеет положительный знак, ток возрастает, т.е. имеет место накопление энергии магнитного поля катушки.

В интервале , напряжение имеет отрицательный знак, т.е. происходит разряд индуктивности.

В момент имеет место максимум напряжения , катушка разряжена и далее идет процесс накопления магнитного поля катушки с обратным знаком и т.д.

Мгновенная мощность равна:

.

Средняя мощность за период равна:

.

Из полученного следует, что потребление активной мощности при протекании синусоидального тока в индуктивности не происходит. Энергия идёт на создание магнитного поля катушки . Имеет место периодические заряд и разряд индуктивного элемента.

Индуктивный элемент называется реактивным.