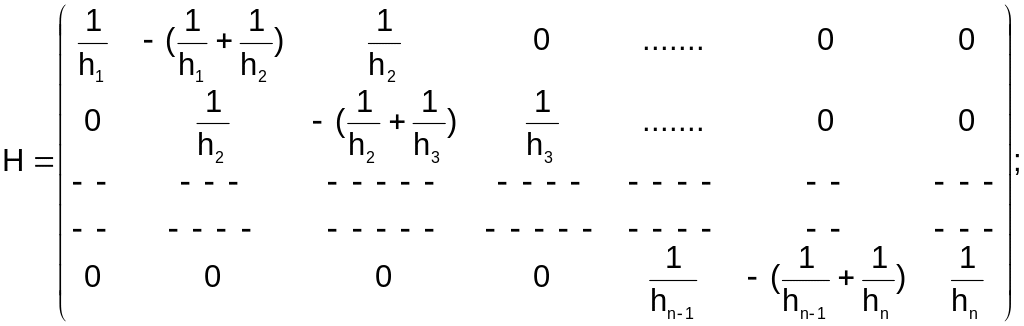- •Требования к выполнению лабораторних работ
- •Постановка задачи
- •Содержание отчета
- •Теоретические сведения
- •Примеры выполнения заданий
- •Расчет в пакете mathcad
- •Постановка задачи
- •Содержание отчета
- •Постановка задачи.
- •Выводы. Теоретические сведения
- •Примеры выполнения заданий
- •Уточнение корня комбинированным методом.
- •Пример вычислений по методу хорд в пакете mathcad.
- •Пример реализации модифицированного метода
- •Варианты лабораторных работ
- •Лабораторная работа № 3 решение алгебраических и трансцендентных уравнений методом простой итерации
- •Постановка задачи
- •Содержание отчета
- •Постановка задачи.
- •Теоретические сведения
- •Примеры выполнения заданий
- •П ример решения трансцендентного уравнения в пакете mathcad.
- •Пример расчета в пакете matlab.
- •Встроенные функции пакетов mathcad, matlab для приближенного решения уравнений Пакет mathcad
- •Пакет matlab
- •Постановка задачи
- •Содержание отчета
- •Теоретические сведения.
- •Выводы. Теоретические сведения
- •Примеры выполнения заданий
- •Пример вычислений в пакете mathcad.
- •Программная реализация метода Гаусса для решения слау в пакете matlab.
- •Варианты лабораторных работ
- •Лабораторная работа № 5 итерационные методы решения системы линейных алгебраических уравнений (слау)
- •Постановка задачи
- •Содержание отчета
- •Постановка задачи.
- •Теоретические сведения.
- •Выводы. Теоретические сведения
- •Пример выполнения заданий
- •Решение системы методом простой итерации.
- •Пример расчета в пакете mathcad.
- •Программная реализация метода простой итерации для решения слау в пакете matlab.
- •Встроенные функции пакетов mathcad и matlab
- •Для приближенного решения систем линейных
- •Алгебраических уравнений
- •Пакет mathcad
- •Пакет matlab
- •Тема 3. Интерполяция и приближение полиномами Лабораторная работа № 6 интерполяционный многочлен лагранжа
- •Постановка задачи
- •Теоретические сведения.
- •Выводы. Теоретические сведения
- •Пример выполнения заданий
- •Построение полинома Лагранжа для таблично заданной функции.
- •Построение полинома Лагранжа в пакете mathcad.
- •Пример построения полинома Лагранжа в пакете matlab.
- •Пример использования узлов Чебышева.
- •Пример вычисления погрешности интерполирования.
- •Варианты лабораторных работ
- •Лабораторная работа № 7 интерполирование для таблиц с постоянным шагом. Численное дифференцирование. Обратное интерполирование
- •Постановка задачи
- •Содержание отчета
- •Постановка задачи.
- •Теоретические сведения.
- •Выводы. Теоретические сведения
- •Пример выполнения заданий
- •Построение первой формулы Ньютона в пакете mathcad.
- •Пример программ для вычислений по первой формуле Ньютона в matlab.
- •Обратное интерполирование с помощью полинома Ньютона в пакете mathcad.
- •Решение задачи обратного интерполирования
- •Варианты заданий
- •Лабораторная работа № 8 интерполирование кубическими сплайнами
- •Постановка задачи
- •Содержание отчета
- •Постановка задачи
- •Теоретические сведения.
- •Выводы. Теоретические сведения
- •Пример выполнения заданий
- •Построение кубического сплайна в пакете matlab.
- •Построение кубического сплайна в пакете mathcad.
- •Варианты лабораторных работ
- •Варианты лабораторных работ (окончание)
- •Встроенные функции интерполирования Пакет mathcad
- •Пакет matlab
- •Библиографический список
- •Содержание
- •Тема 1. Приближенное решение алгебраических
- •Тема 2. Приближенное решение систем линейных
- •Тема 3. Интерполяция и приближение полиномами……50
Варианты заданий
Номер варианта |
Функция |
Точки интерполяции |
|
Номер варианта |
Функция |
Точки интерполяции |
1 |
А |
1 |
16 |
А |
9 |
|
2 |
Б |
2 |
17 |
Г |
6 |
|
3 |
В |
1 |
18 |
Б |
4 |
|
4 |
А |
2 |
19 |
Д |
5 |
|
5 |
Г |
7 |
20 |
Г |
10 |
|
6 |
В |
2 |
21 |
А |
8 |
|
7 |
Б |
5 |
22 |
Д |
2 |
|
8 |
Д |
3 |
23 |
Б |
7 |
|
9 |
А |
3 |
24 |
В |
10 |
|
10 |
Г |
1 |
25 |
Г |
5 |
|
11 |
В |
6 |
26 |
Б |
8 |
|
12 |
Д |
4 |
27 |
А |
5 |
|
13 |
Б |
3 |
28 |
В |
4 |
|
14 |
В |
9 |
29 |
Г |
3 |
|
15 |
Д |
7 |
30 |
Д |
10 |
Точки интерполяции
№ п/п |
|
|
|
|
|
№ п/п |
|
|
|
|
1 |
0,01 |
0,52 |
0,89 |
0,02 |
|
6 |
0,04 |
0,54 |
0,89 |
0,86 |
2 |
0,04 |
0,46 |
0,87 |
0,88 |
|
7 |
0,03 |
0,43 |
0,86 |
0,02 |
3 |
0,05 |
0,41 |
0,86 |
0,03 |
|
8 |
0,02 |
0,43 |
0,87 |
0,86 |
4 |
0,02 |
0,32 |
0,89 |
0,87 |
|
9 |
0,03 |
0,42 |
0,88 |
0,02 |
5 |
0,01 |
0,45 |
0,88 |
0,03 |
|
10 |
0,05 |
0,43 |
0,87 |
0,89 |
Уравнения для решения задачи нахождения корня методом обратного интерполирования взять из лабораторной работы № 2.
Лабораторная работа № 8 интерполирование кубическими сплайнами
Цель работы: научиться решать задачу построения кубического сплайна, для функции, заданной таблично, построить кусочно-полиномиальный сплайн.
Постановка задачи
Построить кубический интерполяционный сплайн для заданной системы точек в среде пакетов MATLAB , MATHCAD.
Графически визуализировать полученные результаты.
Проверить правильность построения с помощью встроенных функций пакетов MATLAB, MATHCAD.
Содержание отчета
Постановка задачи
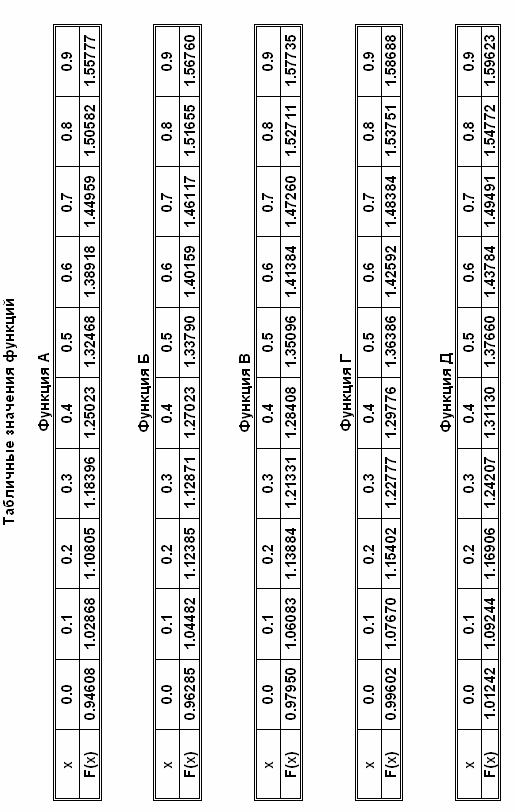
Таблица значений функции.
Теоретические сведения.
Листинги счета на ЭВМ.
Выводы. Теоретические сведения
Интерполяционный полином не всегда дает хороший результат. Например, аппроксимация резонансных кривых колебательных систем дает большую погрешность как на концах кривых (крыльях), так и между узлами. При увеличении степени интерполяционного полинома погрешность только возрастает (явление волнистости). Широкое распространение для решения задачи интерполяции получает аппарат сплайнов. Рассмотрим интерполяцию кубическими сплайнами. В отличии от интерполяции полиномом на каждом участке строится отдельный сплайн.
Пусть на отрезке [a, b] имеется таблично заданая функция a=x0<x1<…<xn =b. Шаг таблицы может быть непостоянным.
Постановка задачи: На отрезке [a, b] необходимо найти функцию g(x), которая удовлетворяет следующим требованиям:
1.
Сплайн g(x)
![]() классу c2(a,b),
т.е.
классу c2(a,b),
т.е.
![]() непрерывны на отрезке [a,b], график g(x) не
имеет острых углов
(т.к.
непрерывны на отрезке [a,b], график g(x) не
имеет острых углов
(т.к.
![]() непрерывна), радиус кривизны определен
в каждой точке.
непрерывна), радиус кривизны определен
в каждой точке.
2.
На каждом участке g(x) является кубическим
полиномом III степени, т.е.
![]() ,
,
где
ai(k)
– коэффициенты сплайна, которые
определимы из дополнительных условий:
![]() – номер сплайна.
– номер сплайна.
3. выполняется основное условие интерполяции:
![]()
![]()
4. вторая производная g''(x) удовлетворяет граничным условиям. В общем случае эти условия зависят от конкретной задачи. Довольно часто используется условие свободных концов сплайнов, а именно g''(a) = g''(b) = 0.
В результате построения с соблюдением всех условий будем иметь
![]()
![]()
Для
определения неизвестных m0…mn
используем непрерывность
![]() В результате получим систему для
определения mk
с n-1 уравнением и n+1 неизвестными. Её
нужно доопределить для однозначного
решения. Дополняем систему граничными
условиями, например условиями свободных
концов сплайна m0
=
mn
=
0.
В результате получим систему для
определения mk
с n-1 уравнением и n+1 неизвестными. Её
нужно доопределить для однозначного
решения. Дополняем систему граничными
условиями, например условиями свободных
концов сплайна m0
=
mn
=
0.
Получаем систему n-1 уравнения с n-1 неизвестными:


В матричном виде систему можно записать следующим образом:
![]() ,
,
где
|
|
|
|
Матрица А – неособенная матрица, система для определения m имеет единственное решение, следовательно, сплайн-функция g(x) однозначно восстанавливается, т.е. задача о нахождении кусочно-кубической функции g(x) имеет единственное решение. Решение системы может быть найдено с помощью метода прогонки (частный случай метода Гаусса) или каким-либо другим способом.