4.4. Модели систем типа Мс

Рассмотрим несколько видов классификационных признаков и соответствующие классы моделей, не претендуя на попытку обоснования их выбора. Заметим только, что сочетания различных классификационных признаков могут образовывать достаточно большое разнообразие практически выделяемых классов моделей.

Аппроксиматоры, называемые также в литературе «черными ящиками» (blackbox),«формальными моделями», являются разновидностью математических моделей, описывают функциональные связи между входами и выходами моделируемой системы без учета (при отсутствии) каких-либо знаний о топологии системы. Коэффициенты таких моделей могут не иметь какого-либо физического смысла, не соотносятся, например, с технологическими параметрами процессов. В этом заключается недостаток таких моделей. Однако, эти модели эффективны в случае невозможности или трудности построения строгих математических описаний поведения систем.

Распространенными примерами таких моделей являются нейронные сети(НС).

Механистические модели. Если знания о функционировании модели формализованы, то для описания таких моделей могут быть использованы механистические модели (ММ), к числу которых относят:

- алгебраические модели (АМ), представляющие собой системы алгебраических и трансцендентных уравнений,

- дифференциальные уравнения (ДУ) и системы ДУ,

- передаточные функции (ПФ),

- логические модели (ЛМ) и др.

Такие модели обычно получают путем анализа физических и химических основ моделируемых процессов. Результатом анализа является прямая илиобратнаямодель процесса. Прямая модель отражает влияние входных координат процесса на выходные и может быть представлена в виде функции

Y=F(X),

где Х и Y- множества входных (в том числе управляющих) и выходных координат соответственно.

В ряде случаев необходимым является получение обратной модели вида

X=Q(Y_н),

где Y_н- множество наблюдаемых или измеряемых значений выходных координат процесса. В большинстве случаев построение обратных моделей является некорректной задачей, т.е. имеющей более одного решения или вообще его не имеющей.

Статистические моделиявляются технологией построения моделей путем описания свойств процесса через статистические переменные и соответствующие статистические оценки этих переменных. По своей сути эти модели содержат элемент неопределенности.

Модели, согласно этой технологии, строятся с использованием методов статистического анализа, теории игр, теории информации и т.п.

Разновидностями данных моделей являются вероятностныеикорреляционныемодели. Вероятностные модели используют плотности вероятности переменных процесса. При этом наиболее часто используются нормальный и экспоненциальный законы распределения. Использование таких моделей ограничено тем, что при числе переменных более двух требуется большое число экспериментов, возникают трудности, связанные с коррелируемостью параметров.

Динамическиемоделии характеристики описывают поведение систем в динамике, т.е. во времени.

Наиболее часто динамические модели представляются линейными и нелинейными дифференциальными уравнениями, разностными уравнениями в частных производных, операторными уравнениями, передаточными функциями и др.

Линейныминазываются элементы, для которых справедлив принцип суперпозиции:

(х₁+ х₂) =(х₁) +(х₂),

где - некоторый оператор.

Таким свойством обладают операторы суммирования, интегрирования, дифференцирования.

При исследовании динамических свойств систем может быть использованы прикладные математические методы операционного исчисления. Например, функционирование некоторой системы описывается ДУ вида

, (4.14)

где х и у - входная и выходная величины. Если в данное уравнение вместо x(t) иy(t) подставить функцииX(s) иY(s) комплексного переменногоsтакие, что

и, (4.15)

то ДУ (4.14) при нулевых начальных условиях равносильно линейному алгебраическому уравнению

a₂ s² Y(s) + a₁ s Y(s) + a₀ Y(s) = b₁ X(s) + b₀ X(s).

Такой переход от ДУ к алгебраическому уравнению называетсяпреобразованием Лапласа, формулы (2.2) соответственноформулами преобразования Лапласа, а полученное уравнение -операторным уравнением.

Новые функции X(s) иY(s) называютсяизображениямидляx(t) иy(t) по Лапласу, тогда какx(t) иy(t) являютсяоригиналамипо отношению кX(s) иY(s).

Переход от одной модели к другой заключается в замене знаков дифференциалов на операторыsⁿ, знаков интеграловна множители, а самихx(t) иy(t) - изображениямиX(s) иY(s).

Для обратного перехода от операторного уравнения к функциям от времени используется метод обратного преобразования Лапласа. Общая формула обратного преобразования Лапласа:

,

где f(t) - оригинал,F(j) - изображение приs=j,j- мнимая единица,- частота.

Преобразование ДУ по Лапласу дает возможность ввести понятие передаточной функции, характеризующей динамические свойства системы.

Например, операторное уравнение

3s²Y(s) + 4sY(s) +Y(s) = 2sX(s) + 4X(s)

можно преобразовать, вынеся X(s) иY(s) за скобки и поделив друг на друга:

Y(s)*(3s²+ 4s+ 1) =X(s)*(2s+ 4),

.

Полученное выражение называется передаточной функцией.

Передаточная функция- это отношение изображения выходного воздействияY(s) к изображению входногоX(s) при нулевых начальных условиях:

.

Передаточная функция для линейных элементов часто является дробно-рациональной функцией комплексной переменной:

,

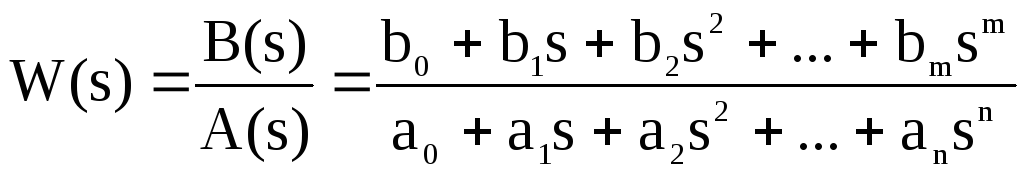где B(s) = b₀ + b₁s + b₂ s² + … + b_m s^m - полином числителя,

А(s) = a₀ + a₁s + a₂ s² + … +a_nsⁿ- полином знаменателя.

Если вместо sподставить выражениеs=j^., получаем преобразование Фурье, которое характеризует связь между частотными характеристиками входных и выходных сигналов элемента. Частотные характеристики дают возможность анализировать описание системы с учетом динамики.

В последнее время более широко используется описание динамики систем методом пространства состояний.

Для описания динамики элементов систем используется в данном методе матричная запись ДУ:

, (4.16)

где А – матрица коэффициентов, U– матрица входов или управлений, Х – матрица пространства состояний:

Х = (х₁, х₂, … х_n)^Т.

В данном случае х_iназывается переменной состояния или фазовой переменной («Т» – символ транспонирования).

Предположим, что динамические свойства объекта описываются ДУ вида

, (4.17)

где a_iиb_i– коэффициенты, у – выходной сигнал,u– входной сигнал объекта.

Если ввести переменные состояния:

и т.д.,

то левая часть ДУ (4.17) примет вид (после деления на (-а_n ):

.

Можно записать уравнение в матричном виде:

.

Решением полученного матричного уравнения является матрица Х.

Для определения выходных параметров y_iуравнение (4.16) дополняется уравнением

Y=C^.X+D^.U,

где С (pn) – матрица связей,D(pq) – матрица обхода,p– число выходных параметров у_i,q– число входных параметровu_i.

Решение матричных уравнений для некоторых случаев может быть произведено аналитически, в частности, для однородного ДУ вида

. (4.18)

Прямое преобразование Лапласа для данного уравнения дает

s^.X(s) –X₀=A^.X(s),

где Х₀– матрица начальных условий, т.е. начальные условия по переменной у, по скорости ее изменения, ускорению и т.д. Отсюда получено

Х(s) =X₀^.[s^.E–A]^-1= Ф(s)^.X_0,

где Е – единичная матрица, Ф(s) – изображение фундаментальной матрицы

Ф(s) = [s^.E–A]^-1.

Оригиналом фундаментальной матрицы является матричный экспоненциал

.

Тогда решение ДУ (4.18) можно получить в виде ряда с шагом tпо времени:

Х₀– начальные условия,

Х(t) = Ф(t)^.Х₀,

Х(2^.t) = Ф(2^.t)^.Х(t) и т.д.

Качественные модели

Существует множество примеров, когда природа процессов принятия решений или функционирования объекта не может быть описана в виде математических соотношений в виду наличия нечетких определений и лингвистических операций или ограничений на технологические параметры и т.д.

Решением этой проблемы является использование качественных моделей, которые наиболее часто представляются в терминах нечетких множеств.