
- •Уфимский государственный нефтяной технический университет
- •А.П. Верёвкин, о.В. Кирюшин
- •Теория систем
- •Учебное пособие
- •1. Системы и задачи их анализа
- •1.1. Свойства систем
- •1.2. Количество информации
- •1.3. Классификация систем
- •2. Элементы теории множеств
- •2.1. Основные понятия и термины
- •2.2. Операции над множествами
- •2.3. Свойства операций над множествами
- •2.4. Алгебры
- •3. Элементы теории графов
- •4. Модели систем
- •4.1. Цели моделирования систем
- •4.2. Уровни моделирования
- •4.2.1. Классификация уровней моделирования
- •4.2.2. Задачи анализа свойств систем, решаемые на концептуальном уровне
- •4.2.3. Задачи, решаемые на топологическом уровне
- •I. Определение структурных свойств системы
- •II. Определение эквивалентных передач
- •III. Выделение подсистем в системе
- •4.2.4. Модели структурного уровня
- •4.2.5. Модели параметрического уровня
- •4.3. Классификация моделей систем
- •4.4. Модели систем типа Мс
- •4.5. Модели требований типа мт
- •5. Современная методология научных исследований и методы системного анализа
- •5.1. Основные понятия
- •5.2. Методология системного анализа
- •5.3. Общая схема принятия решений
- •5.4. Основные этапы приятия решений
- •5.5. Аналитические методы системного анализа
- •5.6. Математические методы
- •5.7. Семиотические методы
- •5.8. Группа экспертных методов
- •5.9. Игровые методы принятия решений
- •5.10. Имитационное моделирование
- •Список использованной литературы
4.5. Модели требований типа мт
Спектр моделей требований весьма широк, т.к. отражает уровень формализованности как целей и критериев, так и моделей принятия решений.
На одном конце этого спектра лежат модели требований для наиболее простых систем принятия решений – регуляторовили простейших видовуправляющих устройств, используемых для формирования управлений в автоматических системах регулирования (АСР), а на другом – схемы экспертного, субъективного, характера.
4.5.1. По своей сути модели регуляторов являются моделями типа Мсмеханистического класса.
Если считать, что информацией является ошибка регулирования
е = х – у,
где х – желаемое значение регулируемого параметра, у – его текущее значение, то управляющее воздействие может формироваться, например, с использованием трех наиболее часто используемых законов:
П-законарегулирования (пропорциональный), для которого управляющее воздействие определяется как
U=K1.e,
где K1– коэффициент усиления регулятора;
И-закона(интегральный), для которого
![]() ;
;
Д-закона(дифференциальный), для которого
![]() .
.
Обычно используются сочетания перечисленных законов регулирования: ПИ- и ПИД-законы.
4.5.2. В более сложных случаях, когда требуется описывать процессы принятия решений с участием человека на тех или иных этапах, эти модели оказываются мало пригодными. Некоторые особенности моделей принятия решений с участием человека рассмотрим на примере оптимизационной задачи, когда решение принимается на основе процедуры оптимизации по множеству показателей или критериев - векторному критерию.
Заметим, что задача формирования управляющих переменных на основе процедуры оптимизации по одному (скалярному) критерию, также как и на основе стандартных законов регулирования, является полностью формализованной и относится к алгоритмическим методам принятия решений.
Векторный критерий состоит из набора (множества показателей), в числе которых могут быть показатели с разными направлениями шкалы полезности.
Направление шкалы полезности связывает категории «больше»-«меньше» с категориями «лучше»-«хуже».
Например, чем выше цена, тем хуже для покупателя, но чем выше качество товара, тем лучше для того же покупателя.
При оптимизации по скалярному критерию решение получается как наилучшее (с учетом ограничений), соответствующее минимуму или максимуму критерия в зависимости от направления шкалы полезности. Иное дело, если показателей несколько.
Рассмотрим задачу выбора решения для случая, когда имеется векторный критерий состоит из двух показателей:
 .
.
Оба показателя имеют одинаковые шкалы полезности: чем меньше, тем лучше. Если для какого-либо показателя направление шкалы не совпадает с установленным, то для изменения направления шкалы полезности вводится показатель вида I’I= 1 /IiилиI’1= -I1(I’I– уровень «плохости»).
Рассмотрим задачу покупки товара наилучшего качества за наименьшие деньги (см. рис. 4.6). Ресурсом оптимизации (варьируемым параметром или параметрами q), от которых зависят значения показателейI1 (q),I2(q) будут варианты товара у разных продавцов.
Движение начнем с произвольного выбора товара, точка 0. Далее будем выбирать товар либо более дешевый и не худшего качества, либо более качественный, но не более дорогой товар.
При этом каждая последующая точка пути соответствует лучшему соотношению цены и качества. В конце концов, наступит момент (точка 3), когда описанную процедуру выполнить не удастся, т.е. одновременное улучшение по двум показателям будет невозможно.
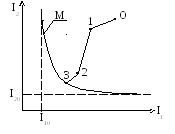
Рис. 4.6
Точка 3 принадлежит множеству решений
М ={q*|arg{Jopt}}
– множеству Парето(множество компромиссов, переговорное множество). Это множество не улучшаемых в смысле векторного критерия решений, (в рассматриваемом случаеopt=min). Существенно, что решение задачи оптимизации по векторному критерию носит принципиально множественный характер и для выбора наилучшего варианта нуженсуперкритерий,который устанавливает приоритеты между показателями. Приоритеты, в конечном счете, устанавливает человек – лицо, принимающее решение (ЛПР).
Существует несколько методов получения решений из множества Парето:
1) метод сворачивания векторного критерия в глобальный скалярный,
2) метод последовательных уступок,
3) метод минимизации по частному критерию или показателю и ряд других.
Метод сворачивания векторного критерия
Сворачивание может производится по одной из следующих форм:
1) Аддитивный критерий
![]() ,
,
где αi– веса (весовые коэффициенты) показателей.
Если показатели имеют разные шкалы или размерности, то для облегчения выбора весов иногда эти показатели нормируют:
![]() ,
,
где
![]() -
минимально (максимально) возможное
значение показателя.
-
минимально (максимально) возможное
значение показателя.
Веса
также нормированы, т.е.
![]() .
.
Физический смысл минимизации такого критерия – это минимизация общих потерь (применений, когда все показатели имеют одинаковый смысл).
2) Линейно-квадратичный критерий
![]() .
.
Минимизация по такому критерию эквивалентна нахождению точки, ближайшей к началу координат (с учетом весов). Физический смысл - минимизация среднеквадратичных (статистических) потерь.
3) Минимаксный (Чебышёвский) критерий
![]() .
.
Физический смысл – минимизация самой большой потери.
4) Модель справедливого компромисса
![]() .
.
Для случая n= 2 имеем α = α1= α2= 0,5 и решение
![]() .
.
То есть относительные потери по одному критерию приводят к относительному выигрышу другого и наоборот.
Метод последовательных уступок
Метод требует большой определенности информации о приоритетах показателей (об их важности). Последовательность применения метода:
1 шаг. Все показатели должны быть расположены в порядке убывания приоритетов.
2 шаг. Отыскивается минимум старшего (наиболее важного) показателя и назначается уступка
I1I1*+I1.
3 шаг.В рамках назначенной уступки проводится минимизация очередного критерия и т.д.:
![]()
![]()
…
![]() .
.
Метод минимизации по частному критерию или показателю
Метод можно рассматривать как вариант предыдущего, если уступки по всем критериям, кроме наименее важного, известны.
Пример
Рассмотрим задачу оптимизации по двум показателям (частным критериям) I1иI2. Допустим, что
 , (4.19)
, (4.19)
где х – переменная (ресурс оптимизации).
Свойства решений задач оптимизации по частным критериям.
Задача 1.I1min.
Область определения х (-, +).
Результат:![]() ,
то есть абсолютный минимумI1достигает при х = 0.
,
то есть абсолютный минимумI1достигает при х = 0.
Задача 2.I2min.
Область определения х (-, -1) и х(-1, +).
![]() при
0. При этомI2-.
при
0. При этомI2-.
На плоскости критериев {I1,I2} =I1I2частным решениям задач 1 и 2 соответствуют точки а(1,1) и с(, -).
Возможные методы получения точек из множества Парето.
I. Метод минимизации одного частного критерия (для данной размерности задачи совпадает с методом последовательных уступок)
 Предположим,
что по критериюI1делается уступка (вводится ограничение)1:
Предположим,
что по критериюI1делается уступка (вводится ограничение)1:
I1 I1* + 1,
где I1* = min I1.
Тогда, как можно видеть из анализа задачи (4.19), существуют два важных случая:
1) При 1< 1 аргумент может изменяться в пределах
х(-1, 1). Решение
задачи:x=arg{xmax},
то есть при![]() решение
будет
решение
будет
![]() и
и![]() .
.
Случаю х (-1, 1) соответствует отрезок кривой между точками А и В (см. рис. 4.7).
2) При 11 решение задачи 2 дает значение х = -1 иI2=I2*, то есть в точке В решение «срывается» в -. Другими словами, при всех11 существует единственное решение х = -1.
II. Метод сворачивания векторного критерия в глобальный скалярный
Выберем аддитивную форму сворачивания:
![]() (4.20)
(4.20)
и попытаемся найти экстремум функции классическим методом:
![]() .
.
Приходим к кубическому уравнению
2.с.х.(х + 1)2= 1 – с, х-1 - из (4.20).
Если представить это уравнение в виде
![]() ,
,
то легко убедиться, что при с = 1 (абсолютный приоритет критерия I1) получается решение х = 0. При с = 0 (приоритетI2) решения не существует.
 Рассмотрим
качественно минимизацию (4.20).
Рассмотрим
качественно минимизацию (4.20).
При некотором с 0 и с1 получается качественно график функцииJ(x) (см. рис. 4.8). Как видно, при неограниченном диапазоне изменения х решение задачи (4.20) и, соответственно, задачи (4.19) будет х = -1.
Если ограничить x> -1, то решение существует сopt, зависящим от с. Причем при уменьшении с (при с0) точка х =arg{minJ} смещается в сторону увеличения.
Для
с << 1 примерное решение:
![]() .
Например, при с = 0,001 имеем х = 10.
.
Например, при с = 0,001 имеем х = 10.
Принятие решения на основе оптимизационной процедуры при известных показателях принципиальных трудностей не вызывает. Неопределенными могут оказаться только приоритеты ЛПР. К сожалению, так бывает очень редко. Обычно имеется неопределенность как в моделях объекта типа Мс, так и в моделях принятия решений (критериях и способах получения решения).
Рассмотрим некоторые виды моделей типа Мт, используемые для принятия решений в более сложных случаях.
К числу таких моделей относится большая группа моделей семиотического типа и группа экспертных методов.
4.5.3. Семиотика – общая теория, исследующая свойства систем знаков, каждому из которых сопоставляется значение. Для семиотического подхода характерны три уровня исследования знаковых систем:
1) синтактика– изучает синтаксис, правила построения и связи в знаковых системах;
2) семантика– изучает интерпретацию, смысл знаковых систем;
3) прагматика– изучает отношения между знаковыми системами и теми, кто их использует.
Теоретическая семиотика изучает совокупность семантики и синтактики, является основой металогики, математических исчислений. Является, в конечном счете, моделью фрагментов мира людей.
В эту группу моделей входят:
- логические модели четкой (конечно-автоматные (КАМ) модели) и нечеткой логики (НЛМ);
- семантические сети (СС);
- продукционные системы (ПС);
- предикатные системы (ПрС) и ряд других.
Рассмотрим некоторые из моделей этой группы.
Логические модели
Конечные автоматы. Логические модели этого типа базируются на алгебре логики. В булевой алгебре используются два элемента «0» и «1» (или {0, 1}).
Примечание: кроме булевой логики имеются также многозначные логики, например, {-1, 0, 1}, а также нечеткие логики, в которых переменные принадлежат значениям 0 и 1 с различной степенью уверенности.
Если используются две переменные Х и Y, принимающие по два значения: 0 = «ложь» и 1 = «правда», то для булевой алгебры определены логические операции (см. табл.4.1):
Таблица 4.1
|
Х |
0 |
0 |
1 |
1 |
Название логической операции |
Обозначение |
|
Y |
0 |
1 |
0 |
1 |
|
в выражениях |
|
|
0 |
0 |
0 |
1 |
- конъюнкция (лог. умножение) |
И, AND,&, *,V |
|
|
0 |
1 |
1 |
1 |
- дизъюнкция (лог. сложение) |
ИЛИ, OR, +, |
|
|
1 |
0 |
0 |
1 |
- тождественность |
=, ~ |
А также функция одного операнда - отрицание (функция «НЕ», NOT, «¬»), например, если Х = 0, то ¬Х = 1.
Существуют и другие функции: стрелка Пирса, штрих Шеффера, импликация и др.
Из булевых переменных и логических операций могут быть построены логические выражения.
Для формирования любой логической формулы достаточно только двух логических операций, одна из которых – отрицание. Для этого применяются законы де Моргана-Шеннона:
![]() и
и ![]() .
.
Для получения логической функции используют таблицу состояния, которая может иметь произвольный вид. Например, см. табл. 4.2.
Таблица 4.2
|
X |
Y |
Z |
F |
|
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Для синтеза логической функции существуют две основные формы записи логических выражений:
1) совершенная дизъюнктивная нормальная форма (СДНФ), представляющая собой дизъюнкцию конъюнкций логических переменных; иными словами, логическая сумма слагаемых, каждое из которых является логическим произведением переменных и называется «термом»:
![]() ,
,
где Di– дизъюнкт (терм),n– число дизъюнктов в выражении;
2) совершенная конъюнктивная нормальная форма (СКНФ), представляющая собой конъюнкцию дизъюнкций, иначе называемую записью по нулю:
![]() ,
,
где Ki– конъюнкт,n– число конъюнктов.
Правило записи выражения в СДНФ: если в строке, где значение функции равно F= «1», какая-либо переменная принимает значение «1», то эта переменная записывается в дизъюнкт в чистом виде, если принимает значение «0», то с отрицанием.

Рис. 4.9
Правило записи выражения в СКНФ: если в строке, где значение функции равно F= «0», какая-либо переменная принимает значение «0», то эта переменная записывается в конъюнкт в чистом виде, если принимает значение «1», то с отрицанием.
Так, для функции Fпо табл. Х имеем СДНФ:
![]()
или то же самое в более простой записи:
![]() .
.
Для упрощения записи логических функций используются:
- логические преобразования,
- карты Карно,
- диаграммы Вейтча,
- методы целенаправленного перебора (алгоритм Мак-Класки).
Рассмотрим метод упрощения полученного логического выражения с помощью карты Карно. Карта Карнопредставляет собой особый вид таблиц состояний, имеющих прямоугольный вид и состоящих из 2nквадратов, гдеn– число входных переменных. Стороны карты помечаются именами переменных таким образом, чтобы половина карты соответствовала «1»-му значению переменной, а другая – «0»-му, причем в карте должны быть учтены все возможные сочетания значений переменных (состояния входов). В результате каждая ячейка карты будет соответствовать определенному набору значений входных переменных. В ячейки заносятся соответствующие значения минимизируемой функции. Так, для рассматриваемого примера карта представлена на рис. 4.9.
Далее для записи выражения в СДНФ производятся объединения ячеек карты, содержащих «1» так, чтобы данные ячейки образовывали прямоугольники или квадраты размером 1, 2, 4, 8, 16 и т.д. ячеек. Каждый такой прямоугольник будет соответствовать своему терму, причем, чем он больше, тем проще будет терм. Прямоугольники могут пересекаться.
После этого записываются термы по принципу: если данному прямоугольнику соответствует «1»-е значение какой-либо переменной, то данная переменная входит в терм в чистом виде; если «0»-е значение, то в инверсном; если соответствует как «1»-е, так и «0»-е, то в терм переменная не входит. Наконец, термы объединяются в логическое выражение с помощью функций дизъюнкции. Для рассматриваемого примера получено выражение, состоящее из трех термов:
![]() .
.
Запись выражений в СКНФ производится аналогично, но объединяются ячейки с нулями. Термы записываются в виде дизъюнкции переменных по принципу: если прямоугольнику соответствует «1»-е значение какой-либо переменной, то данная переменная входит в конъюнкт в инверсном виде; если «0»-е значение, то в чистом; если соответствует как «1»-е, так и «0»-е, то в конъюнкт переменная не входит. После конъюнкты объединяются функциями конъюнкции. Для рассматриваемого примера:
![]() .
.
Из логических выражений подобного вида могут быть образованы логические последовательности, моделирующие процессыпринятия решений.
Элементы теории нечетких множеств и нечеткой логики
Нечеткие множества и логические операции на нечетких множествах (далее НС - нечеткие системы) в последнее время стали завоевывать ведущее положение в системах управления, использующих слабоструктурированную, например, лингвистическую информацию. Они позволяют использовать эвристический опыт управления процессами в тех случаях, когда моделирование процессов принятия решений формальными методами не дает удовлетворительного эффекта. В результате появились технические и программные продукты, выпускаемые ведущими мировыми производителями как бытового, так и технологического оборудования.
В частности, расширение языков программирования промышленных контроллеров на базе нечетких систем (FuzzyLogicProgramming) предложено для стандартаIEC1131.
Нечеткая логика появилась как расширение Булевой логики путем использования логических (нечетких) переменных, принимающих любые значения в интервале [0, 1]. Она была введена доктором Л. Заде (Lotfi Zadeh) в 1960-х годах как способ моделирования неопределенностей естественного языка. Основная идея Заде состояла в том, что человеческий способ рассуждений в большинстве случаев не может быть описан традиционными математическими формализмами. Основная цель нечеткой логики - моделирование человеческих рассуждений и объяснение человеческих приемов принятия решений в ходе решения различных задач.

Рис. 4.10
Основным понятием НС является нечеткая логическая переменная х, которой поставлена в соответствие некоторая функция принадлежности (х),
характеризующая уверенность в принадлежности элемента какому-либо множеству.

Рис. 4.11
Существует несколько типовых видов функций принадлежности (см. рис. 4.12):

Пример. Введем переменную х, характеризующую рост человека.
Допустим, что это лингвистическая переменная означает свойство «высокий». Поскольку представления людей о том, какой рост человека считать высоким четко не определены, данная переменная будет являться нечеткой. Интуитивно полученная зависимость ее значения от роста в метрах может иметь, например, вид (рис. 4.10): для характеристики человеческого роста может быть введено множество переменных Х = {х1, х2, х3, х4, х5}, соответствующих значениям: х1 - «очень низкий», х2 - «низкий», х3 – «средний», х4 – «высокий», х5 – «очень высокий». Соответственно переменным определяются функции (хi), которые могут иметь вид, показанный на рис. 4.11.
Операции над нечеткими множествами:
1) сравнение: А = В, если А(х) =В(х);
2)
дополнение (отрицание):
![]() ,
еслиВ(х) = 1 -А(х);
,
еслиВ(х) = 1 -А(х);
3) пересечение АВ:АВ(х) =min(А(х),B(х));
4) объединение АВ:АВ(х) =max(А(х),B(х));
5)
разность:
![]() ;
;
6) сумма: А+В(х) =А(х) +B(х) –А(х)*B(х);
7) произведение: АВ(х) =А(х)*B(х);
8) концентрация («очень»): con(A)(х) =2А(х);
9)
растяжение («довольно»):
![]() .
.
Системами НЛ называются системы, которые оперируют с нечеткими понятиями и используют при этом нечеткую логику. Системы НЛ могут быть классифицированы на три основных типа:
1) простые (pure),
2) системы Токаги и Суджено,
3) системы с фаззификатором и дефаззификатором (fuzzy).
В простых системахиспользуется механизм нечеткого вывода
![]() ,
,
где R– композиционные правила.
Недостаток простых систем в том, что входные и выходные переменные являются нечеткими.
Системы Токаги и Суджено. Предлагается выходные переменные взвешивать пропорционально значениям входных.
Системы с фаззификатором и дефаззификаторомполучаются из простых систем, если перед применением нечетких операций входные переменные фаззифицировать (перевести в нечеткий вид), а после - дефаззифицировать выходные (преобразовать из нечеткого вида в четкий или аналоговый).
Продукционные системы
Наиболее простым с точки зрения построения и широко используемым типом моделей принятия решений являются продукционные системы. Они представляют собой структурированные наборы продукционных правил (ПП) вида
PR= <S,N,F,AC,W>,
где S- сфера применения данного правила;N- номер или имя правила;F- предусловие применения (условие активизации), содержащее информацию об истинности и приоритетности данного правила;AC- ядро ПП;W- постусловие.
Сфера применения Sобозначает принадлежность ПП какому-либо определенному этапу функционирования ПС или состоянию процесса принятия решения.
В состав правил могут входить условия активизации F, которые представляют собой либо переменную, либо логическое выражение (предикат). КогдаFпринимает значение «истина», ядро продукции может быть активизировано. ЕслиF«ложно», то ядро не активизируется.
Постусловие Wописывает, какие изменения следует внести в ПС, и актуализируется только после того, как ядро продукции реализовалось.
Интерпретация ядра может быть различной в зависимости от вида А и С, находящихся по разные стороны знака секвенции «». Прежде всего, все ядра делятся на два типа:детерминированныеинедетерминированные. В детерминированных ядрах при актуализации ядра и при выполнимости А правая часть ядра выполняется обязательно; в недетерминированных ядрах В может выполняться с определенной вероятностью. Таким образом, секвенция «» в детерминированных ядрах реализуется с необходимостью, а в недетерминированных - с возможностью.
Наиболее часто в ПС используют детерминированные ПП вида
«если А то С»,
где А и С - логические выражения, которые могут включать в себя другие выражения; А называется антецедентом, С -консеквентом.
ПП могут быть доопределены логическими выражениями, определяющими инициируемые процедуры, которые имеют место в случае отсутствия ее активности:
«если А то С1иначе С2».
Продукционные правила, используемые в СУ, учитывают накладываемые ограничения, а также показатели эффективности, по которым определяются управляющие воздействия и которые часто являются неизмеряемыми лингвистическими переменными.
Достоинствами продукционных систем являются:
- удобство описания процесса принятия решения экспертом (формализация его интуиции и опыта);
- простота редактирования модели;
- прозрачность структуры.
ПС в качестве моделей применимы в следующих случаях:
- не могут быть построены строгие алгоритмы или процедуры принятия решений, но существуют эвристические методы решения;
- существует, по крайней мере, один эксперт, который способен явно сформулировать свои знания и объяснить свои методы применения этих знаний при принятии решения;
- пространство возможных решений относительно невелико (число решений счетно);
- задачи решаются методом формальных рассуждений;
- данные и знания надежны и не изменяются со временем.
Сети Петри
Сети Петри(СП) являются примером семантических сетей, представленных разновидностью ориентированных двудольных графов. Двудольный граф включает вершины двух типов: позиции (обозначаются кружками) и переходы (обозначаются планками). Сеть Петри может быть формально представлена как совокупность множеств:
N= (P,T,G,),
где P= {p1,p2…pn} – множество всех позиций (n– количество позиций),
Т = {t1,t2…tm} – множество переходов (m– количество переходов),
G= (Gp-t,Gt-p) – множество дуг сети:
Gp-t= (pt),Gt-p= (tp) – множества дуг, ведущих соответственно от переходов к позициям и от позиций к переходам (дуг, соединяющих однородные вершины, не существует),
= {1,2…k} – множество весов дуг (k– количество дуг).
Каждая позиция может быть маркирована, т.е. содержать некоторое число фишек. Если обозначить числа фишек, находящихся в i-й позицииpi, какmi, то маркировка всей сети:M= {m1,m2…mn}. Тогда полное определение сети Петри, включая данные о начальной маркировке, можно записать в виде
PN= (N,M0),
где М0– начальная маркировка сети.
При моделировании процессов принятия решений с помощью СП ее позиции интерпретируют собой некоторые условия, состояния, значения переменных и т.д. Переходы интерпретируют собой логические предложения (принятие решений), соответствующие выполнению действий, при этом входные позиции – условия выполнения действий, выходные позиции – результат выполнения действий. Действие (переход) связано с принятием какого-либо решения, которое инициировано определенными условиями и результатом которого является новое состояние (условие).
Пример. Схема принятия решений при попытке получить деньги из банкомата (см. рис.4.13).

Рис. 4.13
Смысл позиций: Р1– карта (ее наличие); Р2– исправность банкомата; Р3– введенный код; Р4– код набран правильно, запрашивается сумма; Р5– код набран неправильно; Р6– сумма доступна; Р7– сумма недоступна (нет такого количества денег на карте); Р8– деньги (получены). Смысл переходов:t1– банкомат принимает карту и делает запрос в банк, ввод кода;t2– запрос суммы;t3– повторный ввод кода;t5– выдача сообщения о недоступности суммы;t6– выдача денег;t7– повторный набор суммы;t8– забрать карту из банкомата (другой исход: имеется другая карта, с которой также нужно снять деньги – см. дуги, обозначенные пунктиром);t9– выдача сообщения, что код неверный.
Роль указателей мощности потоков выполняют фишки или метки (●). Формально метка – это знак выполнения соответствующего условия. Переход срабатывает только в том случае, если во всех входных позициях имеется достаточное количество меток (по меньшей мере, по одной). При срабатывании перехода из входных позиций изымаются метки (в случае взвешенной СП изымается количество меток, соответствующее весам дуг, связывающих входные позиции с данным переходом), а во входные – добавляются (для взвешенной СП – также соответственно весам дуг). Начальная маркировка СП есть начальное состояние системы.
Таким образом, если осуществить начальную маркировку СП, то использованием формальных правил можно описать логику работы системы и произвести анализ ее работоспособности. Переходы меток описываются графом достижимости (ГД), у которого каждой вершине соответствует определенная маркировка, а каждой дуге – переход, который срабатывает при данной маркировке.
Таким образом, граф достижимости представляется как
GD= (V,E),
где V– массив вершин (маркировок, соответствующих вершинам):
V= {М1, М2 … Мq},
Мi–i-я маркировка,q– количество маркировок;
Е = {e1,e2 …ep} – массив дуг, связывающих вершины (р – количество дуг).
Каждая дуга представляется как совокупность ei= {1,2, Т}, где1и2– номера начальной и конечной вершин графа; Т = {t1,t2, …tk} – массив переходов, соответствующий дуге;k– количество одновременно срабатывающих переходов при переходе от одной маркировки к другой.
Алгоритм построения графа по исходной СП:
1. За исходную берется маркировка М0и ей присваивается метка «новая».
2. Для каждой «новой» маркировки выполнять следующие операции:
2.1. Для «новой» маркировки Мновопределяются все переходы, которые могут быть запущены, а также все возможные комбинации этих переходов.
2.2. Для каждого разрешенного перехода или комбинации переходов производятся следующие действия:
2.2.1. Определяется маркировка М’, которая образуется при срабатывании данного перехода (комбинации переходов).
2.2.2. Просматриваются все маркировки на пути от М’ к начальной М0. Если на пути находится маркировка М”, элементы которой больше либо равны соответствующим элементам новой и которая не равна М’, то вместо элементовm’i, которые больше, чем элементыmiмаркировки М0, записывается символ «» (бесконечность). В массив Е записывается дуга с соответствующими1,2и Т.
2.2.3. Просматриваются все маркировки графа. Если находится маркировка, равная новой, то в массив Е записывается новая дуга, у которой 1=2и равны номеру найденной маркировки.
Т аблица
4.3
аблица
4.3
-
(Р1Р2Р3Р4Р5Р6Р7Р8)
М1
(11000000)
М2
(00100000)
М3
(00010000)
М4
(00000100)
М5
(00000001)
М6
(00001000)
М7
(00000010)
2.2.4. Если в п.п. 2.2 и 2.3 маркировки не найдены, то создается новая вершина графа, в которую записывается новая маркировка, в массив Е записывается дуга, у которой 1равна номеру исходной маркировки,2- номеру новой маркировки, Т – набор переходов, срабатывание которых привело к переходу от одной маркировки к другой. Далее определяется массив всех разрешенных переходов и расчет продолжается, начиная с п. 2.2.
Для рассмотренного выше примера СП граф ГД имеет вид (см. рис. 4.14), список маркировок приведен в табл. 4.3.С помощью ГД могут быть определены свойства СП и, в конечном счете, моделируемой системы. К ним относятся:
- живость (отсутствие тупиковых состояний);
- ограниченность (сеть ограниченна, если символ «» не входит ни в одну вершину графа);
- безопасность (сеть безопасна, если в метки вершин входят только «0» и «1») – физически безопасность означает отсутствие зацикливаний;
- правильность (если сеть безопасная и живая, то она правильная);
- обратимость (сеть обратима, если в графе имеется хотя бы одна дуга, направленная к начальной маркировке М0);
- пассивность переходов (переход tiпассивен, если он не соответствует ни одной дуге графа);
- число возможных состояний Nсост.
Сеть Петри называется k-ограниченной, если в любом состоянии в любой позиции скапливается не болееkфишек.
Любая система должна представляться правильной сетью.
Для рассмотренного примера можно сделать вывод, что сеть правильная, обратимая и без пассивных переходов.
Практическое значение и наиболее ясную интерпретацию имеют два вида СП:
1) Маркированные графы– каждая позиция такой СП должна иметь не более одного входного и одного выходного перехода;
2) А-сети(автоматные сети) – каждый переход такой СП должен иметь не более одной входной и одной выходной позиции.
СП моделируют очень широкий класс логических задач. Существует много разновидностей сетей. Главное их достоинство – возможность анализировать логический процесс по неизбыточным моделям. Кроме того, формализованные методы анализа СП в сочетании с возможностью декомпозиции дают возможность решать очень сложные задачи принятия решений.
Методология SADT
Примером реализации семантической сети (см. раздел 5.4) является методология SADT(Structure Analysis and Design Technique), которая реализуется в различных автоматизированных программных пакетах анализа и конструирования для целей структуризации и формализации процессов принятия решений в организационных системах. В частности, широко известна так называемаяIDEF-методология построения моделей систем, согласно которой модель системы представляется в виде совокупности трех моделей:
- IDEF0 – функциональной модели, отображающей причинно-следственные связи между функциями и подфункциями в системе;
- IDEF1X– информационная модель, показывающая структуру информации;
- IDEF/CPN – динамическая модель, базирующаяся на так называемых раскрашенных СП (ColoredPetriNet) и позволяющая просматривать и анализировать систему с точки зрения динамики.
В терминах IDEF0 модель системы представляется в виде комбинации блоков и дуг. Блоки используются для представления функций системы и сопровождаются текстами на естественном языке. Дуги представляют множества объектов(как физических, так и информационных) или действия, которые образуют связи между функциональными блоками. Место соединения дуги с блоком определяет тип интерфейса.
Управляющие выполнением функции данные входят в блок сверху, в то время как информация, которая подвергается воздействию функции, показана с левой стороны блока; результаты выхода показаны с правой стороны. Механизм (человек или автоматизированная система), который осуществляет функцию, представляется дугой, входящей в блок снизу (рис. 4.15).

Рис. 4.15
Важнейшая цель информационной модели заключается в выработке непротиворчивой интерпретации данных и взаимодействий между ними с тем, что необходимо для интеграции, совместного использования и управления целостностью данных.
Появление понятий концептуальной схемы данных привело к методологии семантического моделирования данных, т.е. к определению значений данных в контексте их взаимосвязей с другими данными.
Методология IDEF1X - один из подходов к семантическому моделированию данных, основанный на концепции "Сущность - Отношение" (Entity-Relationship ), это инструмент для анализа информационной структуры систем различной природы. Информационная модель, построенная с помощью IDEF1X-методологии, представляет логическую структуру информации об объектах системы. Эта информация является необходимым дополнением функциональной IDEF0-модели, детализирует объекты, которыми манипулируют функции системы.
Концептуально IDEF1X-модель можно рассматривать как проект логической схемы базы данных для проектируемой системы. Основными объектами информационной модели являются сущности и отношения.
Сущность представляет множество реальных или абстрактных предметов (людей, объектов, мест, событий, состояний, идей, пар предметов и т.д.), обладающих общими атрибутами или характеристиками. Отдельный элемент этого множества называется "экземпляром сущности". Каждая сущность может обладать любым количеством отношений с другими сущностями.
Сущность является "независимой", если каждый экземпляр сущности может быть однозначно идентифицирован без определения его отношений с другими сущностями.
Сущность называется "зависимой", если однозначная идентификация экземпляра сущности зависит от его отношения к другой сущности.
Сущность обладает одним или несколькими атрибутами, которые либо принадлежат сущности, либо наследуются через отношение, обладает одним или несколькими атрибутами, которые однозначно идентифицируют каждый образец сущности и может обладать любым количеством отношений с другими сущностями модели.
Если внешний ключ целиком используется в качестве первичного ключа сущности или его части, то сущность является зависимой от идентификатора. И наоборот, если используется только часть внешнего ключа или вообще не используются внешние ключи, то сущность является независимой от идентификатора.
Пример независимой сущности приведен на рис. 4.16, зависимой - на рис. 4.17.

Рис. 4.16
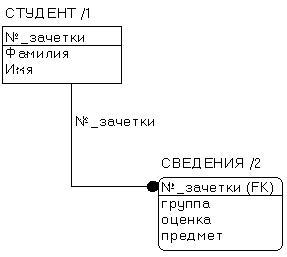
Рис. 4.17
Динамическая модель (IDEF/CPN) осуществляет проверку функциональной модели системы путем преобразования ее в СП. При этом функциональным блокам ставятся в соответствие переходы СП, а дугам – позиции.
4.5.4. Группа экспертных моделей представляет собой, по существу, схемы организации опроса экспертов и принятия решений. Конкретные методы из группы экспертных моделей рассматриваются в разделе 5.5.
