4.2.4. Модели структурного уровня

Различают модели элементов в статике и в динамике.

Моделями статикиявляются функции вида

y=f(x),

где хиусоответственно входные и выходные координаты системы, которые не зависят от времени или их значения рассматриваются как установившиеся (t).

f– функция, которая может задаваться аналитически, графически или алгоритмически.

Динамическиемодели и характеристики описываются линейными и нелинейными дифференциальными уравнениями, разностными уравнениями. уравнениями в частных производных, операторными уравнениями, передаточными функциями и др.

4.2.5. Модели параметрического уровня

Прежде, чем говорить о задании параметров, необходимо сказать, что параметры могут быть измерены в разных шкалах. Существует четыре уровня измерений:

1) шкала наименований(примеры: Иванов, Эверест,…);

2) шкала порядка– имеется признак, по которому производится сравнение, но не обязательно в виде числа (пример: холодно – тепло – горячо);

3) шкала интервалов– используются числа, характеризующие разности границ интервалов (пример: температура в гр. Цельсия или Фаренгейта);

4) шкала отношений.

Для шкал 3-го и 4-го уровней справедливы группы аксиом:

1) аксиомы тождественности

А = В (или А В),

если А = В, то В = А,

если А = В и В = С, то А = С;

2) аксиомы рангового порядка(для их выполнения требуется, чтобы выполнялось условие сравнимости и транзитивности; например, нельзя сравнивать бифштекс с книгой)

если А > B, тоB<A,

если А > В и В > С, то А > С (то же для нестрогого порядка);

3) аксиомы аддитивности

если А = Р и В > 0, то А + В > Р,

А + В = В + А,

если А = Р и В = Q, то А + В =P+Q,

(А + В) + С = А + (В + С).

Кроме переменных, измеряемых действительными числами, существуют комплексные числа, задаваемые парой (а,в) действительных чисел, одно из которых (а) условно измеряет действительную, а второе (в) - мнимую составляющую.

Кроме того, существуют также переменные, измеряемые нечеткими, лингвистическими «числами», характеризуемые парой (х, _х), где х нечеткая переменная,_х - функция принадлежности к какому-либо множеству. С помощью таких переменных измеряют (оценивают) человеческие ощущения. Данные числа сложно отнести к какому-либо из вышеперечисленных типов и следует согласиться, что это особый тип чисел.

4.3. Классификация моделей систем

Одна из возможных классификаций моделей, используемых в процессе анализа и синтеза (создания) систем, представлена на рис. 4.5.

Среди моделей различного вида и назначения выделяются два принципиально различных типа:

-первый тип предназначен для описания характеристик (свойств) систем, т.е. для целей анализа;

-второй тип предназначен для принятия каких-либо решений с целью достижения целей.

В дальнейшем эти типы моделей будем условно обозначать как Мс– модели систем иМт – модели требований. Рассмотренные выше примеры моделей, в основном, могут быть отнесены к типу Мс.

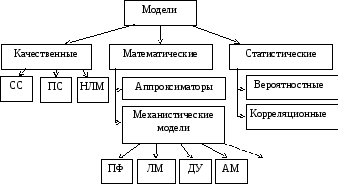
Рис. 4.5

Основными элементами моделей типа Мт являются:

• -цели и критерии, по которым осуществляется выбор решения;

• модели принятия решений: законы регулирования и управления, алгоритмы формирования управлений, схемы и процедуры принятия решений и т.д.

Все возможные варианты постановки задач построенияцеленаправленных систем являются бинарными отношениями (декартовым произведением) этих двух типов моделей

S = Мс  Мт.

Далее в п.п. 4.4 и 4.5 будут рассмотрены некоторые виды моделей типов МсиМт.