
- •Уфимский государственный нефтяной технический университет
- •А.П. Верёвкин, о.В. Кирюшин
- •Теория систем
- •Учебное пособие
- •1. Системы и задачи их анализа
- •1.1. Свойства систем
- •1.2. Количество информации
- •1.3. Классификация систем
- •2. Элементы теории множеств
- •2.1. Основные понятия и термины
- •2.2. Операции над множествами
- •2.3. Свойства операций над множествами
- •2.4. Алгебры
- •3. Элементы теории графов
- •4. Модели систем
- •4.1. Цели моделирования систем
- •4.2. Уровни моделирования
- •4.2.1. Классификация уровней моделирования
- •4.2.2. Задачи анализа свойств систем, решаемые на концептуальном уровне
- •4.2.3. Задачи, решаемые на топологическом уровне
- •I. Определение структурных свойств системы
- •II. Определение эквивалентных передач
- •III. Выделение подсистем в системе
- •4.2.4. Модели структурного уровня
- •4.2.5. Модели параметрического уровня
- •4.3. Классификация моделей систем
- •4.4. Модели систем типа Мс
- •4.5. Модели требований типа мт
- •5. Современная методология научных исследований и методы системного анализа
- •5.1. Основные понятия
- •5.2. Методология системного анализа
- •5.3. Общая схема принятия решений
- •5.4. Основные этапы приятия решений
- •5.5. Аналитические методы системного анализа
- •5.6. Математические методы
- •5.7. Семиотические методы
- •5.8. Группа экспертных методов
- •5.9. Игровые методы принятия решений
- •5.10. Имитационное моделирование
- •Список использованной литературы
3. Элементы теории графов
При изложении предыдущего материала уже были использованы модели в виде графов. Наряду с теоретико-множественным описанием моделей систем представление в виде графов является одним из наиболее распространенных.
ГрафГ – геометрическая фигура, построенная на множестве вершинV= {v1,v2, …vm} и реберR= {r1,r2, …rn}:
Г = (V,R). (3.1)
Если ребра ориентированы, то их называют дугами, а граф - ориентированным (орграфом). При этом вершины называютсяузлами.

а) б)
Рис. 3.1
Примеры использования графов для моделирования:
1. Неориентированные графы описывают (моделируют) дороги между населенными пунктами А, B,CиD(см. рис. 3.1, а).
2. Орграф описывает однонаправленные каналы передачи информации (см. рис. 3.1, б).
Дуга ri, связанная с зломvj, называетсяинцидентнойэтому узлу, причем, если заходит – положительно инцидентная, если выходит – отрицательно инцидентная.
Два узла vkиviсмежны, если им инцидентна одна дуга. Аналогично, две дуги смежны, если они инцидентны одному узлу, причем, если одна выходит, а другая заходит – последовательно смежны, в противном случае - параллельно смежны.
Дуга, выходящая из узла и в нее же заходящая, называется петлей.
Узел, из которого дуги только выходят, называется истоком, а в который только заходят –стоком. Узлы сток и исток – висячие узлы.
Две системы S1иS2с заданными на них отношениямиR1иR2изоморфны, если:
1) их структурные элементы попарно взаимно однозначно соответствуют друг другу;
2) подмножество элементов А1системыS1связано отношениемR1, тогда соответствующее подмножество (см. п. 1) А2системыS2связано отношениемR2.
Существует гомоморфизм – упрощенная модель исходной системы, т.е. не выполняются какие-либо из вышеуказанных условий.
Связи в системе можно изображать двояко:
1) элементы – это вершины, а связи – дуги (вершинныйграф),
2) элементы – дуги, а связи – узлы (реберныйилисигнальныйграф).
Структуры графов можно представить как графически, так и структурными матрицами. Известны три вида структурных матриц, изоморфных графической модели графа: матрицы смежности, инцидентности (инциденций) и структуры связей.
Матрица
смежности– квадратная матрица А =
{aij},![]() ,
гдеm– число узлов, т.е.
Аmxm, для которой
,
гдеm– число узлов, т.е.
Аmxm, для которой
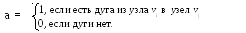
Число единиц в матрице А равно числу дуг n.
Эта матрица обладает интересным свойством: если возвести матрицу А в k-ю степень, то каждый элемент матрицы Аkбудет равен числу путей из узлаviв узелvjдлиной вkдуг.
Путь в графе – это последовательность последовательно смежных дуг, ориентированных в одном направлении.
Пример 3.1.

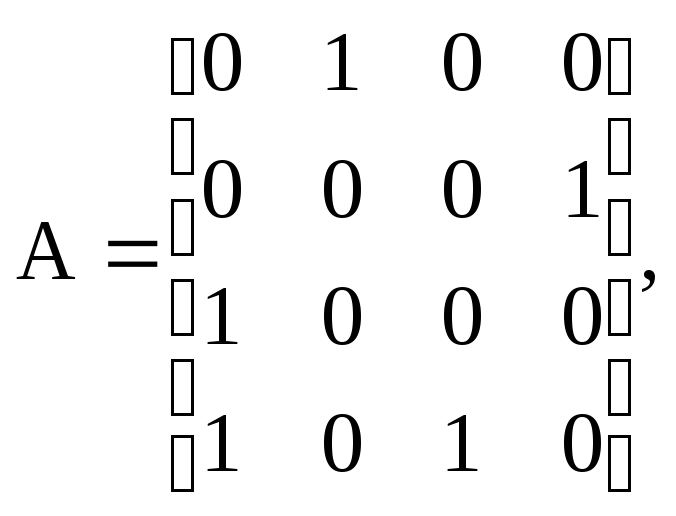
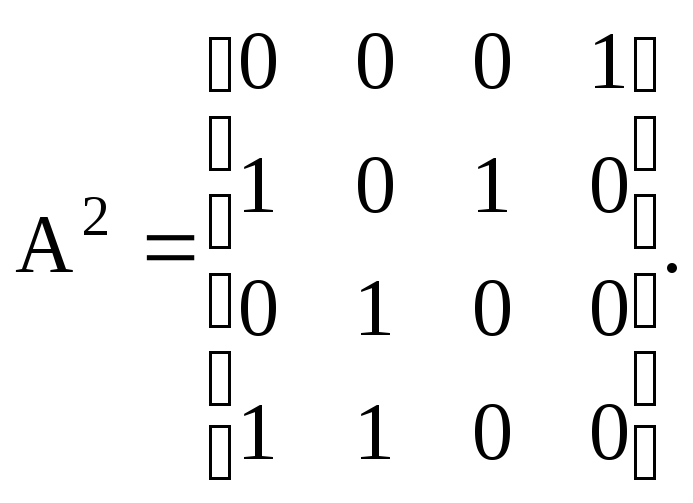
Как видно (см. рис. 3.2), через две (k= 2) смежные дуги можно попасть: из вершины 1 в вершину 4, из 2 в 1, из 2 в 3, из 3 в 4, из 4 в 1 и из 4 в 2.
Таким образом, можно алгоритмически определить, существует ли путь из viвvjдлиной вkдуг. Очевидно, что если число узловm, максимальная степеньk, в которую нужно возвести А для определения самого длинного пути, равна (m– 1).
Матрица
инцидентности– в общем случае
прямоугольная матрица В = {bij},![]() ,
,![]() ,
гдеm– число вершин,n– число ребер. Для орграфов:
,
гдеm– число вершин,n– число ребер. Для орграфов:
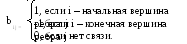
Для неориентированных:
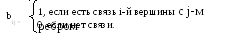
№№ вершин


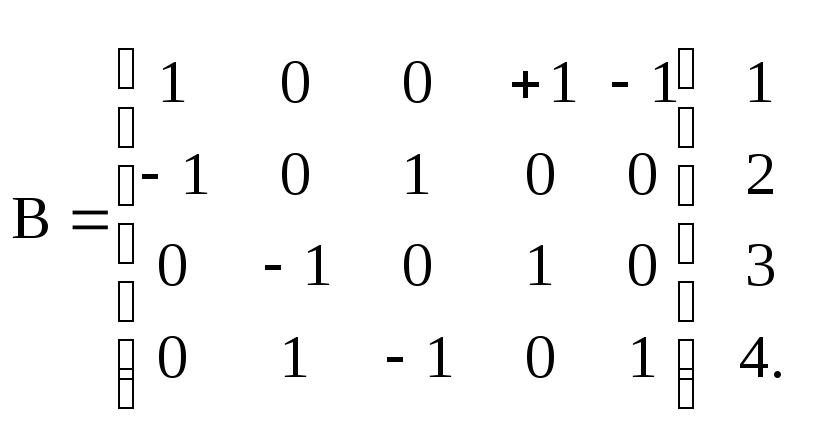
Матрица структуры связейС = {cij} устанавливает отношения между дугами:
С = ВТВ,
С – симметрическая матрица размером nxn, т.е. Сnxn, для которой
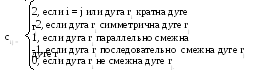


Рис. 3.3
Таким образом, матрица структуры связей содержит информацию о взаимной ориентации пар дугграфа.
Кроме этого, могут использоваться структурные матрицы, кодирующие отдельные свойства графов:
- наличие контуров (контур = замкнутый путь),
- наличие путей,
- отношения касания.
Касающимисяназываются пути, контуры или пути с контурами, если они содержат хотя бы один общий узел.
Сильносвязаннымназывается граф, в котором любой узел достижим из любого другого узла.
Достижимость– это существование пути из узлаviв узелvj. Например, на рис. 3.3 путь из узла 1 в узел 4 имеет вид:
узел 1 W1узел 2W2узел 3W4узел 4.

 Может
оказаться, что не все узлы достижимы из
остальных узлов. В этом случае может
быть выделен подграф Г1, т.е.
совокупность, подмножество узлов, для
которого условие сильной связности
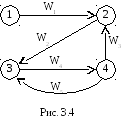
выполняется. Например, граф Г (см. рис.
3.4) не сильносвязный, т.к. в узел 1 из узлов
2, 3 и 4 нет путей. Сильносвязной компонентой
Г1для графа Г состоит из узлов 2,
3 и 4 с соответствующими дугамиW2–W5.
Может
оказаться, что не все узлы достижимы из
остальных узлов. В этом случае может
быть выделен подграф Г1, т.е.
совокупность, подмножество узлов, для
которого условие сильной связности
выполняется. Например, граф Г (см. рис.
3.4) не сильносвязный, т.к. в узел 1 из узлов
2, 3 и 4 нет путей. Сильносвязной компонентой
Г1для графа Г состоит из узлов 2,
3 и 4 с соответствующими дугамиW2–W5.
Физический смысл сильной связности – наличие обратных связей (ОС) между всеми узлами или, другими словами, взаимозависимость (взаимовлияние) всех переменных в графе.
Важность понятия «сильная связность» вытекает из того, что практически все целенаправленные системы строятся на основе принципа обратной связи, когда информация о выходных величинах (координатах) некоторого объекта используется для формирования управляющего сигнала Uэтим объектом.
Структура простейшей системы управленияописывается графом (см. рис. 3.5), гдеW1можно интерпретировать как модель объекта управления, аW2– модель управляющего устройства. Узлы 1 – управлениеU, 2 и 4 можно интерпретировать как выходную величину объекта у, 3 (ε) –ошибка регулирования, узел 5 – задание х (желаемое значение величины у).

W2
Рис. 3.5
