Фізичний аналіз

Фізичну систему утворює ідеальний газ. Початковий та кінцевий стан системи відомі. Виходячи з цього, можна визначити зміну внутрішньої енергії ( ), тому що вона не залежить від виду процесу.

Враховуючи, що процеси, в яких бере участь газ, квазістатичні, параметри проміжного стану системи можна обчислити за допомогою газових законів, а потім визначити роботу, яку виконує система, і кількість теплоти за першим законом термодинаміки.

Розв’язання

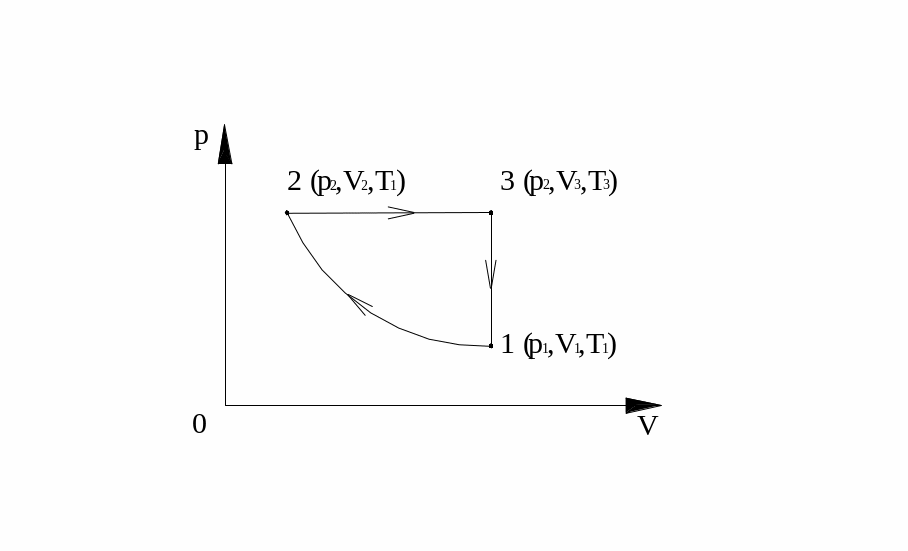
Розглянутий процес зображується на діаграмі двома відрізками прямих – ізохорою – та ізобарою , де - проміжний стан, який характеризується параметрами . Користуючись рівнянням стану, легко показати, що , оскільки маса азоту залишається сталою, то в точках 1 та , наприклад, матимемо: , звідки . Аналогічно , звідки (див. умову).

1. Визначимо зміну внутрішньої енергії.

Згідно з рівнянням внутрішньої енергії

,

де - число молів азоту.

Оскільки згідно з рівнянням стану ідеального газу

- для стану 1,

- для стану 2,

то ,

тоді .

Після обчислення за цією формулою одержимо Дж.

2. Обчислимо кількість теплоти.

При ізохорному та ізобарному процесах кількості теплоти дорівнюють відповідно:

,

.

Шукана сумарна теплота процесу дорівнює:

Оскільки

, , а ,

то:

.

Після обчислення одержимо:

(Дж).

Як бачимо, в результаті переходу азот віддає теплоту зовнішньому середовищу.

Шукана робота , тому що при ізохорній зміні стану . Отже, згідно з рівнянням .

Після обчислення одержимо: Дж.

Робота від’ємна, як це й повинно бути при стиcкуванні газу.

Задача 5. На якій висоті густина повітря при температурі С зменшується порівняно з густиною на рівні моря вдвічі? Температуру газу вважати сталою.

С, К
- ?

Фізичний аналіз

Фізична система – повітря, що знаходиться у полі тяжіння Землі, тому розподіл молекул повітря підпорядковується закону Больцмана. При розв’язанні задачі повітря будемо вважати ідеальним газом.

Розв’язання

Для розв’язання задачі будемо використовувати барометричну формулу

, (1)

де - тиск газу на висоті ,

- тиск на висоті .

Густину газу визначимо з рівняння стану ідеального газу

, (2)

(3)

Підставляючи (2) і (3) в (1), одержимо:

, тоді

.

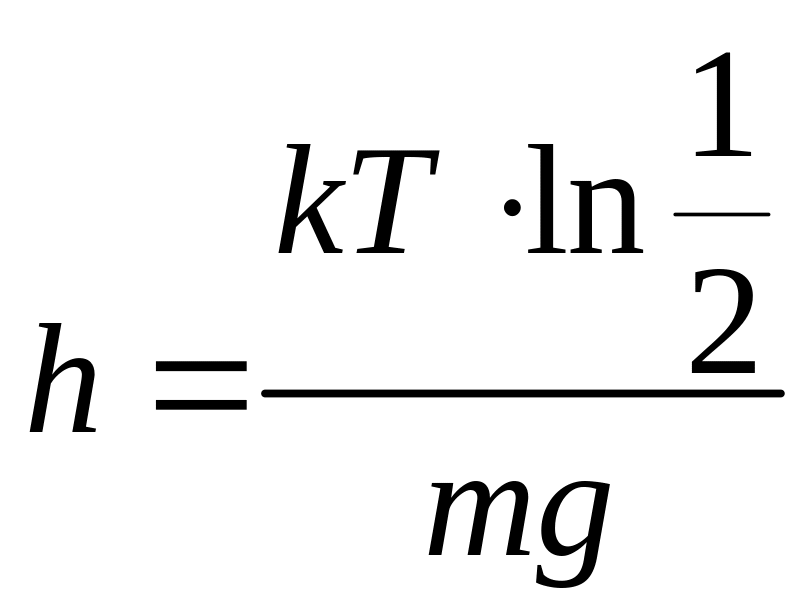Після обчислення за цією формулою одержимо: км.

Задача 6. Обчислити зміну ентропії азоту масою кг, що охолоджується від температури К до К при сталому об’ємі.

кг К К
- ?

Фізичний аналіз

Фізична система – азот масою . Фізичний процес полягає у зміні ентропії газу, що відбувається при ізохорному процесі. Процес є квазістатичним та оборотним.

Розв’язання Визначимо зміну ентропії, що відбувається в системі, за формулою:

,

де - кількість теплоти, що її віддає система при охолодженні.

Цю зміну кількості теплоти визначимо з I-го початку термодинаміки

.

Для ізохорного процесу , тому

.

Тоді .

Кількість ступенів вільності азоту .

Після обчислення за цією формулою одержимо: Дж/К (знак “-” свідчить про те, що у цьому процесі ентропія зменшується).

Приклад 7. Один моль ідеального газу здійснює цикл, який складається з ізотерми, ізобари та ізохори. Обчислити ККД циклу.

(2-3) (3-1)
-?