29. Что такое функция распределения св? Что такое плотность вероятности св? Приведите ее свойства.

Плотностью вероятности (плотностью распределения вероятностей) непрерывной СВ X называют функцию

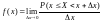. (1.3)

Из свойства 4 функции распределения имеем:

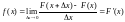(1.4)

Итак, плотность вероятности равна производной от функции распределения (поэтому иногда ее называют дифференциальной функцией распределения).

Свойства плотности вероятности:

1. .

2. .

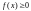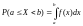3. Если f(х) – плотность вероятности непрерывной СВ, то функция распределения .

4. .

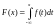30. Как рассчитывается вероятность попадания св в определенный интервал с помощью функции распределения, с помощью плотности вероятности?

Можно отметить, что для непрерывной СВ справедливы равенства

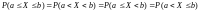(1.5)

На рис. 1.2 и 1.3 изображены характерные графики функции распределения и плотности вероятности непрерывной СВ.

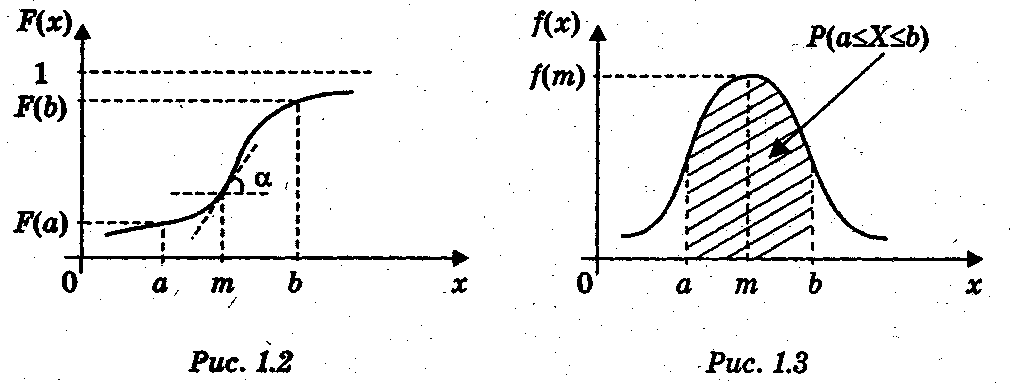
Из свойств функции распределения и плотности вероятности нетрудно заключить, что 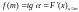( 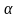–- угол наклона касательной к кривой F(x) в точке х = m). Площадь под графиком кривой плотности вероятности f(x) равна единице. Площадь S заштрихованной фигуры на рис. 1.3 равна: 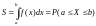. Вероятность попадания значений СВ в «хвосты» распределения, т.е. в интервалы 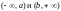, равна .

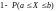Таким образом, с помощью плотности вероятности f(x) непрерывной СВ X можно определить вероятность ее попадания в заданный интервал: 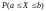, что имеет большое прикладное значение.

36 Что такое дерево вероятностей? Сформулируйте правила построения и проверки корректности дерева вероятностей?

Использование деревьев вероятностей может упростить определение сложных вероятностей, связанных с несколькими взаимозависимыми событиями. Дерево вероятностей представляет собой графическое отображение затронутых вероятностей.

Дерево вероятностей — это рисунок, на котором показаны безусловные и ус­ловные вероятности для комбинаций двух и более событий. Рассмотрим сначала пример, для которого дерево вероятностей уже построено, и проследим детали его построения. Дерево вероятностей тесно связано с деревом решений, которое широко используют в финансах и других областях коммерческой деятельности.

Пример. Управление поддержкой программного обеспечения

Поддержка программного обеспечения — достаточно сложный вид деятельности. Некоторые пользовате­ли звонят, чтобы попросить совета, как работать с программой. Другим необходимо помочь разрешить проблемы, с которыми они столкнулись во время работы. Представьте себе, что в качестве руководителя отдела поддержки вы количественно описали вероятности некоторых характерных звонков пользовате­лей и изобразили свои результаты в виде дерева вероятностей, показанного на рис. 6.5.1.

Рис. 6.5.1 содержит много информации. Будем рассматривать его слева направо. Прежде всего отметим, что вероятность события "пользователь раздражен" составляет 0,20 (это значит, что 20% всех обратив­шихся за помощью были раздражены, а 80% — нет).

Условные вероятности записаны на рисунке над четырьмя ветвями дерева, расположенными прямо под надписью "Получил ли пользователь помощь?". Обратите внимание, что 15% раздраженных пользова­телей помощь получили (это вероятность события "пользователь получил помощь" при условии события "пользователь раздражен"), а 85% раздраженных пользователей помощи не получили. Ниже нарисова­ны две другие ветви. Они свидетельствуют о том, что помощь получили 70% "нераздраженных" пользо­вателей и не получили помощь 30% таких пользователей. Явно видно, что отдел поддержки лучше справляется с оказанием помощи пользователям, которые при обращении не высказывают своего раз­дражения (соотношение получивших помощь пользователей для этих групп составляет 70% к 15%).

Числа в кружках в правой части рис. 6.5.1 показывают вероятности различных событий, сформированных путем комбинирования и и не. Вероятность того, что пользователь был раздражен и получил помощь, со­ставляет 0,03. Это означает, что 3% всех пользователей были раздражены и получили при этом помощь. Далее, 17% всех пользователей были раздражены и помощи не получили; в 56% случаев пользователи не были раздражены и помощь получили, а 24% пользователей не были раздражены и помощи не получили.

Из представленного на рисунке дерева можно найти любую из представляющих интерес вероятностей. Вероятность события "пользователь раздражен" приведена в первом столбце обведенных в кружок чисел (0,20), а вероятность противоположного события, "не раздражен", показана в кружке, расположенном непосредственно ниже. Вероятность события "пользователь получил помощь" находим сложением двух помещенных в кружочках справа вероятностей, характеризующих получение помощи: 0,03 + 0,56 • 0,59. Условная вероятность события "пользователь получил помощь" при условии наступления события "пользователь раздражен" приведена над соответствующей ветвью дерева, она равна 0,15. Несколько сложнее найти вероятность события "пользователь раздражен" при условии события "пользователь по­лучил помощь". Для этого можно воспользоваться определением условной вероятности.

Таким образом, из всех пользователей, которым сотрудники отдела оказали помощь, раздраженными при обращении были 5,1 %. Другой способ найти эту условную вероятность состоит в том, чтобы построить новое дерево вероятностей, начинающееся не с события "пользователь раздражен", а с события "пользователь получил помощь", поскольку для того, чтобы представить некоторую условную вероятность, информацию, задающую условие, необходимо разместить в дереве перед этой условной вероятностью.

Правила построения дерева вероятностей

Для построения дерева вероятностей прежде всего необходимо нарисовать са­мо дерево, затем записать на рисунке всю известную для данной задачи инфор­мацию и, наконец, воспользоваться основными правилами, чтобы вычислить не­достающие числа и закончить дерево.

1. Вероятности указываются в каждой из конечных точек и обводятся кружоч­ками. На каждом уровне дерева сумма этих вероятностей должна равняться 1 (или 100%). Так, например, на рис. 6.5.1 сумма вероятностей на первом уров­не составляет 0,20 + 0,80 = 1,00 и на втором уровне — 0,03 + 0,17 + 0,56 + 0,24 = 1,00. Это правило помогает заполнить один пустой кружок в столбце, если значения всех остальных вероятностей этого уровня известны.

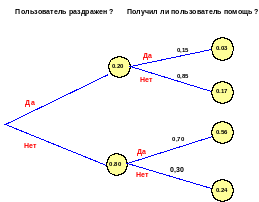
Рис. 6.5.1

2. Условные вероятности указываются рядом с каждой из ветвей (кроме, возможно, ветвей первого уровня). Для каждой из групп ветвей, выходящих из одной точки, сумма этих вероятностей также равна 1 (или 100%). Например, на рис. 6.5.1 для первой группы ветвей получаем 0,15 + 0,85 = 1,00 и для второй группы — 0,70 + 0,30 = 1,00. Это правило позволяет вычислить одно неизвестное значение условной вероятности в группе вет­вей, исходящих из одной точки.

3. Обведенная кругом в начале ветви вероятность, умноженная на условную вероятность рядом с этой ветвью, дает вероятность, записанную в круге в конце ветви. Например, на рис. 6.5.1 для верхней ведущей вправо ветви имеем 0,20 х 0,15 = 0,03, для следующей ветви — 0,20 х 0,85 = 0,17; аналогичные соотношения выполняются и для других двух ветвей. Это правило можно использовать для вычисления одного неизвестного значения вероятности из трех, соответствующих некоторой ветви.

4. Записанное в круге значение вероятности равно сумме обведенных кружками вероятностей на концах всех ветвей, выходящих из этого круга вправо. Так, например, для рис. 6.5.1 из круга со значением 0,20 выходят две ветви, на концах которых находятся обведенные кружками вероятности, сумма которых равна этому значению: 0,03 + 0,17 = 0,20. Это правило позволяет найти одно неизвестное значение вероятности в группе, включающей эту вероятность и все вероятности на концах ветвей дерева, выходящих из соответствующего круга.

Используя эти правила можно, зная все, кроме одного значения вероятности для некоторой ветви или на некотором уровне, находить это неизвестное значение.