26. В каких случаях применяют формулу Байеса? (Показать на примерах)

Теорема. Вероятность произведения двух независимых событий, равна произведению вероятностей этих событий, т.е.

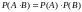
Правила вычисления условной вероятности при наличии дополнительной информации

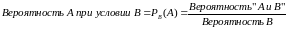
ПРИМЕРЫ

1. Рассмотрим в качестве примера вероятности роста или паде­ния двух биржевых индексов. События не являются взаимоисключающими, поскольку очевидно, что оба индекса могут опус­каться и подниматься одновременно. Предположим, что индекс _{FTSE 100} может возрасти с вероятностью 0,55 и упасть с вероят­ностью 0,45. Также предположим, что в тот же интервал времени индекс _{S&P 500 возрастет} с вероятностью 0,35 и может упасть с вероятностью 0,65. Существует также вероятность, равная 0,3, что оба индекса возрастут одновременно. Какова вероятность того, что индекс _{FTSE 100} или _{S&P 500} возрастет?:

2. Если два фондовых индекса не влияют друг на друга своими изменения­ми, то их ковариация равна нулю, и, следовательно, они незави­симы. Однако следует отметить, что ковариация между основ­ными индексами обычно отличается от нуля.

Тем не менее представим, что индексы _{FTSE 100} и _{S&P 500} не зависит друг от друга. Какова будет тогда вероятность того, что оба индекса возрастут одновременно?

Отсюда вероятность одновременного возрастания обоих ин­дексов будет

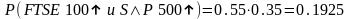
3. Применим правило умножения для зависимых событий в случае с двумя фондовыми рын­ками, если между изменениями их индексов существует положи­тельная или отрицательная ковариация. Каждое изменение со­стояния рынка — это событие, а условная вероятность — это вероятность роста или падения рынка, обусловленная падением или ростом другого рынка. Мы знаем, что _{FTSE 100} и _{S&P 500}

не являются независимыми друг от друга, (коэффициент корреляции между ними равен 0,793). В нашем примере вероятность роста _{FTSE 100} в следующий момент времени и роста _{S&P 500} равна 0,3. Мы также знаем, что вероятность роста _{FTSE 100} равна 0,55. Отсюда можно вывести вероятность роста _{S&P 500} , обусловленную ростом _{FTSE 100} :

^{Т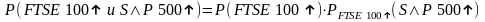 о есть .}

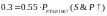^{Таким образом, вероятность}

27. В каких случаях применяют формулу Бернулли? (Показать на примерах)

§ 1. Испытания Бернулли.

Теория вероятностей имеет дело с такими экспериментами, которые можно повторять, по крайней мере теоретически, неограниченное число раз. Пусть некоторый эксперимент повторяется n раз, причем результаты каждого повторения не зависят от исходов предыдущих повторений. Такие серии повторений часто называют независимыми испытаниями. Частным случаем таких испытаний являются независимые испытания Бернулли, которые характеризуются двумя условиями:

1. результатом каждого испытания является один из двух возможных исходов, называемых соответственно «успехом» или «неудачей»;

2. вероятность «успеха» в каждом последующем испытании не зависит от результатов предыдущих испытаний.

Теорема Бернулли. Если производится серия из n независимых испытаний Бернулли, в каждом из которых успех появляется с вероятностью р, то вероятность того, что успех в n испытаниях появится ровно m раз , выражается формулой

P_n(m)=C_n^mp^mq^n-m, где q=1-p – где вероятность неудачи.

Эта формула называется формулой Бернулли.

Задача 1. Игральная кость бросается 6 раз. Найти вероятность того, что ровно 3 раза выпадет «шестерка».

Решение. Пятикратное бросание кости можно рассматривать как последовательность независимых испытаний с вероятностью успеха («шестерки») равно 1/6 и вероятностью неудачи — 5/6. Искомую вероятность найдем по формуле .

Задача 2. Монета бросается 6 раз. Найти вероятность того, что герб выпадет не более, чем 2 раза.

Решение. Искомая вероятность равна сумме трех вероятностей

Р = Р₆(0) + Р₆(1) + Р₆(2) = .