
- •Глава 8. Представление знаний в виде фреймов
- •8.1. Логики знания и фреймы
- •Эпистемическая модальность
- •Деонтическая модальность суждений
- •Алетические модальности
- •Вывод с умолчаниями в немонотонных логиках
- •Α(х):Мβ1(х),...,βm(х) γ(х)
- •Ограничение — форма немонотонного вывода
- •Структура знания и структуры крипке
- •Байесовский подход
- •Извлечение знаний из текстов
Алетические модальности
Алетические модальности — это выраженная в суждении, в терминах необходимость — случайность либо возможность - невозможность информация о логической или фактической детерминированности суждения. В естественном языке показателями суждений возможности являются слова: «возможно», «может быть», «не исключается», «допускается». Например: договор купли-продажи жилого дома с условием пожизненного содержания продавца может быть расторгнут по требованию продавца, если покупатель не исполняет обязанностей, принятых на себя по этому договору. Возможность обозначается знаком 0, необходимость — знаком . Детерминированные суждения в модальных терминах возможности и невозможности выражаются следующим образом.
Необходимость
р эквивалента невозможности
![]() p:
p:
p
=
![]() ◊O
◊O![]() р.
р.
Возможность
р эквивалента отрицанию необходимости
![]() p:
p:
◊p
=
![]()
![]() р.
р.
Вывод с умолчаниями в немонотонных логиках
Логики
умолчаний введены для умозаключений,
являющихся всего лишь правдоподобными.
При неполной информации мы вынуждены
получать всего
лишь правдоподобные, предположительные
заключения. Для того чтобы учесть
изменения в логическом описании ситуации,
возникающие по мере поступления новых
знаний, в логике умолчаний предлагается
следующее расширение логики исчисления
предикатов первого порядка. Логика
с умолчаниями
∆-
это пара <W,D>,
где W
- множество формул исчисления предикатов
первого порядка (ИП) и D
- множество умолчаний или правил вида
А: М В/С (где А, В и С - ИП формулы и М
является сокращением для слова
«совместно»). Правила умолчания следует
читать «Если А известно и
![]() B
невыводимо, тогда выводи С». Идея состоит
в том, что W
представляет неполное
описание мира и D
представляет множество метаправил,
используемых
для того, чтобы создать расширение
описания. Например:
B
невыводимо, тогда выводи С». Идея состоит
в том, что W
представляет неполное
описание мира и D
представляет множество метаправил,
используемых
для того, чтобы создать расширение
описания. Например:
Предприятие(х): М является прибыльным (х)
является прибыльным (х)
что читается как «большинство предприятий являются прибыльными». Система логики умолчаний представляется теорией с умолчаниями, состоящей из некоторого множества особо выделенных формул и правил вывода. В ней содержатся формулы логики предикатов, представляющие основную часть информации, обрабатываемую в соответствии с имеющимися аксиомами. Содержатся также правила умолчаний, отражающие различные утверждения, касающиеся исключений. Логики умолчаний позволяют формализовать рассуждения в виде правил вывода, называемых умолчаниями. Правило умолчания D — это выражение вида:
Α(х):Мβ1(х),...,βm(х) γ(х)
где α(х), β1(x),...βm(x),γ(x) — формулы языка ИП, свободные переменные у которых выбраны среди х - (x1...,xn), α(х) называется требованием умолчания, |βi(х) — обоснование умолчания Di, i = 1,...,т, γ(х) — следствие умолчания D, М — некий символ метаязыка. Интуитивный смысл таков: если мы верим в α(х) и если β1(x), ..., βт(х) выполнимо вместе со всем, во что мы верим, то можно верить и в у(х).
Умолчание
D
называется замкнутым тогда и только
тогда, когда α(х), β1
(х), ..., βm(x),
γ(Х) не содержат свободных переменных.
Свободные переменные
умолчания считаются
![]() -квантифицированными.
Область действия этих
кванторов простирается на все члены
умолчания. Незамкнутое умолчание
называется открытым. Его конкретизацией
является замкнутое умолчание,
полученное заменой всех свободных
переменных открытого умолчания на
константы языка ИП.
-квантифицированными.
Область действия этих
кванторов простирается на все члены
умолчания. Незамкнутое умолчание
называется открытым. Его конкретизацией
является замкнутое умолчание,
полученное заменой всех свободных
переменных открытого умолчания на
константы языка ИП.
Теория с умолчаниями подразумевает некоторое (нулевое или большее) число множеств предложений, которые выводимы с использованием множества формул W и удовлетворяют свойству выполнимости. Эти множества предложений называются расширением данной теории с умолчанием. Расширение — это надмножество основных сведений, включающее все выводимое по правилам классической логики и/или логики умолчаний.
Применение
правил умолчания в различном порядке
может порождать различные варианты
расширения, например набор высказываний
<{A![]() B},
{:M
B},
{:M![]() A/
A/![]() A,:M
A,:M![]() B/
B/![]() B}>
дает в одном варианте расширение,
содержащее А и
B}>
дает в одном варианте расширение,
содержащее А и
![]() B
и расширение, содержащие В и
B
и расширение, содержащие В и![]() А.
Расширения должны быть внутреннесовместны,
но как можно видеть из примера, два
различных расширения могут
быть несовместны. Теория с умолчаниями
может иметь нуль или более расширений,
каждое из которых является минимальным
множеством Е со следующими
свойствами.
А.
Расширения должны быть внутреннесовместны,
но как можно видеть из примера, два
различных расширения могут
быть несовместны. Теория с умолчаниями
может иметь нуль или более расширений,
каждое из которых является минимальным
множеством Е со следующими
свойствами.
Любое расширение Е содержит W.
Е замкнуто относительно монотонной дедукции.
Е нечувствительно к умолчаниям (если A: MB/C
 D
и А
D
и А Е
и B
Е
и B D
тогда
С
D
тогда
С D).
D).
Доказательство в теории с умолчаниями определяется следующим образом. Пусть f — замкнутая формула ИП. Конечная последовательность D0,.. .,Dk есть доказательство для f в ∆ тогда и только тогда, когда:
l.W U{KC(D0)}├f,
2.W U{KC(Di)}├ КТ(Di-1)для1=1,2,...,k,
Dk
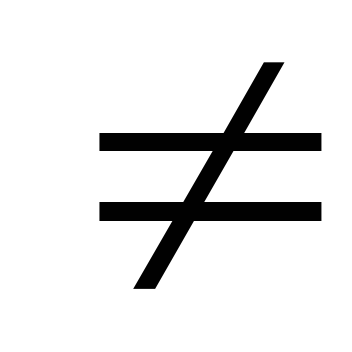 ø,
ø,W U {KC(Di)}/0 < i < k} выполнимо, где KC(Di) — конъюнкция следствий и KT(Di) — конъюнкция требований умолчаний из Di, таким образом доказательство есть последовательность подмножеств умолчаний.
Пусть X — подмножество W, Thw(x) — множество замкнутых формул, общезначимо выводимых из X по классическим правилам вывода из W:
Thw(x)
= {w
│w
![]() W,
w
— замкнута и X
├w}.
W,
w
— замкнута и X
├w}.
Пусть ∆ = (W,D) — теория с умолчаниями, S — подмножество в W. Обозначим F(S) — наименьшее подмножество в W, удовлетворяющее следующим трем условиям:
W![]() Г(S),
Г(S),
Thw(Г(S)),
если
![]()
Множество
формул E![]() W
является расширением для А тогда и
только тогда,
когда Г(Е) = Е, т.е. Е — неподвижная точка
оператора Г.
W
является расширением для А тогда и
только тогда,
когда Г(Е) = Е, т.е. Е — неподвижная точка
оператора Г.
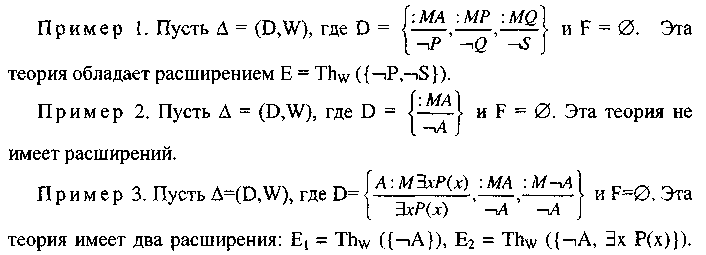
Некоторые теории с умолчаниями не обладают расширениями. Они состоят из нормальных умолчаний.
