3.3. Техника вывода

Вывод заключается в порождении новых фактов и знаний из уже имеющихся в базе данных посредством применения правил вывода. Основным инструментом вывода является представление знаний в форме правил следующего вида:

IF <ситуация > THEN <действие >. Это же правило основное в реализации выводов из хранимых фактов. Вывод — это разновидность знания, а именно, знания о том, как можно извлечь из базы данных эксплицитно представленных знаний, дополнительные знания, не представленные эксплицитно.

Стратегии вывода. Существуют два общих типа стратегий вывода: в прямом направлении и обратном направлении. Чтобы объяснить эти стратегии, правила базы данных преобразуются в ациклический AND/OR орграф. Орграф означает направленный граф, в то время как дуга на фигуре указывает отношение AND.

На графе вывода стратегия прохода вперед начинается с процесса вывода путем опроса фактов о листьях, таких как отрасли промышленности, процент задолженности и темпы роста. При условии, что эти данные определены, задолженность и рост выводятся прослеживанием направленных узлов. Итерации продолжаются до тех пор, пока не будет достигнуто определенное заключение, по получении которого вывод заканчивается. Система продвижения вперед по графу иногда называется стратегией снизу вверх или вывод, управляемый данными

Возвратная стратегия начинается с корневой вершины, чтобы подтвердить, удовлетворяет или нет эта вершина определенному утверждению. Если заданы некоторые факты, значение их истинности получается прослеживанием направленных вершин. Итерации продолжаются до тех пор, пока не будет достигнуто определенное заключение относительно истинности этих фактов, в этот момент вывод заканчивается. Стратегия вывода вперед иногда называется стратегией сверху вниз или стратегией выводов, управляемых правилами.

Возможности логического вывода — основной процесс системы, основанной на знаниях. При дедуктивном выводе знания представляются на языке логики как множество формул (аксиом) А. Рассмотрим простой пример вывода

Рассмотрим следующие три элемента знания, каждый из которых представлен в двух или более формах:

К1. У каждого человека существует отец: ua FATHER(a.u), что можно записать в более краткой форме как ua FA (a,u) или a FA (а,и).

К2. Дед является отцом отца: xyz (FA(z,y)  FA(y,x)  G(z,x).

КЗ. У каждого есть дед: bv G(v,b).

Первое из утверждений приведено как на естественном языке, так и в виде предложения формализованного языка исчисления предикатов первого порядка, которое читается следующим образом: «Для любого u существует а такое, что а есть отец u.»

Рис 3.6. Дерево вывода утверждения КЗ «у каждого есть бед»

методом резолюций

Чтобы сделать формулу более наглядной, символы предикатов, такие как FATHER часто сокращают и опускают скобки, если это не приводит к неоднозначности. Кванторы общности могут опускаться по соглашению.

Как можно заметить, КЗ действительно является логическим следствием К1 и К2. Таким образом, система с дедуктивными способностями может просто хранить К1 и К2 в базе знаний, но пользователь может также получить доступ к КЗ. В качестве правила вывода используется правило резолюции.

Чтобы применить метод резолюций, наши три формулы должны быть подвергнуты некоторым механическим подготовительным преобразованиям к так называемой клаузальной форме. Это преобразование начинается с отрицания формулы

FG К1К2 —> КЗ или эквивалентной ей формулы К1К2  КЗ Логические символы, отличные от ,  и  в литералах замещаются согласно хорошо известным правилам, включающим сколемизацию экзистенциально связанных переменных.

Наконец, преобразование к конъюнктивной нормальной форме в нашем случае дает следующий набор клозов:

{FAzy, FAyx, Gzx} {FA(fu,u)} {Gvb} — множество из трех клозов (интерпретируемое как их конъюнкция), каждый из которых состоит из множества литералов, интерпретируемого как их дизъюнкция, f и b-сколемовские функции в этом случае. Удивительно, что только совсем недавно был предложен алгоритм с линейной, а не экспоненциальной сложностью преобразования формул к сколемовской нормальной форме. Можно заметить, что отрицание FG — излишний шаг. Если мы исключим его, то получим:

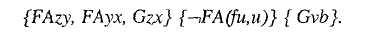
Резолюция теперь разрешает любой из двух клозов, формируя их объединение в качестве нового клоза после удаления пары литералов, которые могут быть сделаны взаимно дополнительными посредством унификации соответствующих термов. Подстановка v вместо z и b вместо х унифицирует термы в двух литералах с предикатным символом G. Этот процесс повторяется итеративно до тех пор, пока мы не получим пустой клоз, свидетельствующий об успешном завершении доказательства. Мы покажем такое резолютивное доказательство для нашего примера вместе с подстановкой, выполняемой на каждом шаге на рис. 3.6.

В процессе вывода важную роль играют Хорновские дизъюнкты, которые по крайней мере в одном литерале не имеют знака отрицания. Наш пример состоит фактически из Хорновских дизъюнктов.

При оценке запросов знания представляются множеством определений D и интерпретацией, которая дает связывает множества примитивных предикатных символов с отношениями базы данных. Запрос — это формула Q(v) со свободными переменными v. Пусть Q(v)/D означает результат подстановки определения произвольных символов в Q(v). Результат обработки запроса — это множество инстанциаций S такое, что Q(s)/D — истинно при интерпретации.