20.Основные этапы нейросетевого анализа. Классификация известных нейросетевых структур по типу связей и типу обучения и их применение [1/1].

Тип обучения Тип связей	Обучение «с учителем»	Обучение «без учителя»
Без обратной связи	Многослоный персептрон (задачи классификации и аппроксимации)	Сети Кохонена конкурентные сети (задача кластеризации и сжатия данных)
С обратной связью	Рекуррентные аппроксиматоры (задача прогнозирования)	Сети Хопфильда (задачи кластеризации, оптимизации, ассоциативная память)

Основные этапы нейросетевого анализа:

Этап 1: Подготовка исходных данных. Формирование обучающей выборки. (Данные должны быть не противоречивыми).

Этап 2: Необходим выбор типа архитектуры НС.

– Выбор типа нейрона со своей функцией активации.

– Выбор количества входов и выходов, что связано с постановкой задачи.

– Выбор количества слоев и нейронов в каждом слое.

Этап 3: Подготовка данных.

– Кодирование входов/выходов.

– Нормировка данных (если необходимо).

– Обеспечение независимости между входами нейросети – предобработка данных

Этап 4: Процесс обучения сети.

Этап 5: Выбор нейросети, который наилучшим образом подходит по результатам обучения для решения задачи.

Этап 6: Оценка значимости ошибки, которую дает нейронную сеть для решения поставленной задачи.

В случае если нас не устраивает результат, то возвращаемся к этапу 2.

21. Алгоритм обучения с учителем для многослойного персептрона [1/1]

М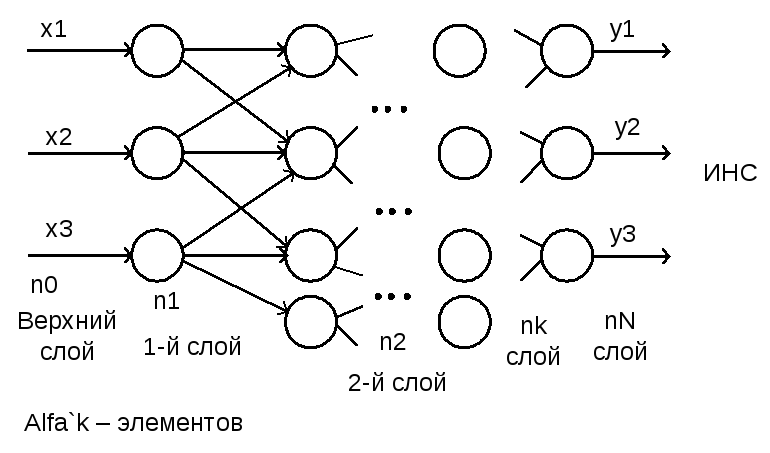ногослойный персептрон – искусственная нейронная сеть, в которой имеется несколько слоев нейронов с настраиваемыми весами связи.

Нейроны входных слоев принимают синоптические сигналы от нейронов предыдущих слоев.

- значение выходного сигнала j к-го слоя.

1-й слой , 2-й слой, …, к-й слой, выходной слой.

Обучение искусственной нейронной сети включает 2 этапа: 1) прямое распространение входного обучающего образа. 2) вычисление ошибки и ее образа распространения. 3) регулирование весов.

Этот метод основан на вычислении вектора градиента поверхности ошибок, который указывает на направление кратчайшего спуска по поверхности из данной точки. Последовательность шагов приводит после ряда итераций к минимуму поверхности ошибок. Алгоритм основан на ∆-правиле, которое гласит: «Корректировка весов на текущем шаге обучения осуществляется в направлении антиградиента функции ошибок». Минимизируемая функция ошибок:

, где - реальное выходное состояние нейронаj выходного слоя нейросети при подаче на ее входы k-го образа; - требуемое, целевое выходное состояние этого нейрона.;

;

22. Алгоритмы обучения нейронных сетей. Алгоритм обратного распространения ошибки [1/1]

Под обучением понимается целенаправленное изменение весовых коэффициентов синоптических связей нейронов сети из условий достижения требуемых характеристик сети, т.е. желаемая реакция на входные воздействия. В основе лежит базовый принцип обучения – минимизация эмпирической ошибки между желаемым выходом сети и фактической реакции сети. Теорема Розенблатта: Для любого данного набора входной векторов и любой требуемой их классификации алгоритм обучения через конечное число шагов приведет к вычислению требуемого набора весов, если таковой существует.

Существует 2 алгоритма обучения: 1) с учителем; 2) без учителя.

Обучение с учителем: обучение, которое производится под контролем внешнего «учителя», который оценивает поведение системы и управляет ее последующими модификациями. Используется в сетях, предназначен-ных для решения задач классификации, аппроксимации, прогнозирования. Обучение без учителя: Сеть путем самоорганизации делает необходимые изменения. Применяется в задачах кластеризации и сегментации для поддержки принятия решений.

Процедура обратного распространения ошибки.

Обучение искусственной нейронной сети включает 2 этапа: 1) прямое распространение входного обучающего образа. 2) вычисление ошибки и ее образа распространения. 3) регулирование весов.

Этот метод основан на вычислении вектора градиента поверхности ошибок, который указывает на направление кратчайшего спуска по поверхности из данной точки. Последовательность шагов приводит после ряда итераций к минимуму поверхности ошибок. Алгоритм основан на ∆-правиле, которое гласит: «Корректировка весов на текущем шаге обучения осуществляется в направлении антиградиента функции ошибок». Минимизируемая функция ошибок:

, где - реальное выходное состояние нейронаj выходного слоя нейросети при подаче на ее входы k-го образа; - требуемое, целевое выходное состояние этого нейрона.;

;