6. Определения четких и нечетких множеств. Определение нечеткого множества. Функция принадлежности. Примеры нечетких дискретных и непрерывных множеств. [1/2]

Нечеткость – понятие, относящееся к таким множествам, в которых возможны градация степени принадлежности к ним, от полной принадлежности до полной не принадлежности, т.е. такой класс объектов в котором нет резкой границы между объектами с полной принадлежностью к нему и его окружением.

Четкое множество – множество, которое задано в виде множества пар

, где X€AcX, - функция принадлежности

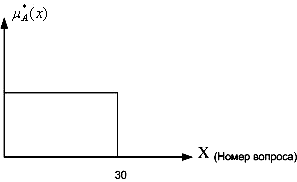
Нечеткое множество считается заданным, если задано множество пар

В нечетком множестве вводится понятие функции принадлежности , которая показывает степень принадлежности элементаX множеству A.

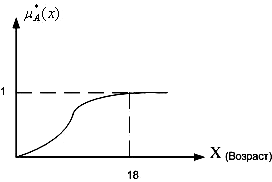
Существует также нечеткие дискретные множества, которые формируются при известной функции

*6. Определения четких и нечетких множеств. Определение нечеткого множества. Функция принадлежности. Примеры нечетких дискретных и непрерывных множеств. [2/2]

Например подходящая температура купания на море

Четкое множество в теории множеств:

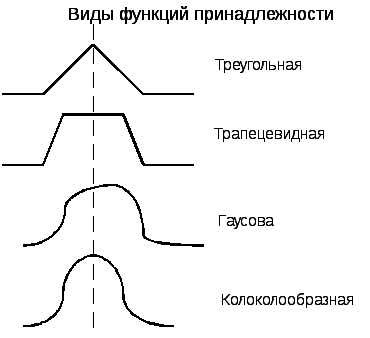
Выбор функции принадлежности осуществляется двумя способами:

а) Прямой. Группа экспертов непосредственно определяют виды и параметры функции принадлежности, основываясь на особенностях предметной области.

б) Косвенной. Проводит опрос экспертов, в процессе которого они отвечают на да или нет.

7. Основные свойства нечетких множеств. Нечеткое число и нечеткий интервал.[1/3]

1. Носитель (основание) нечеткого множества А – множество тех элементов х для которых функция принадлежности>0.

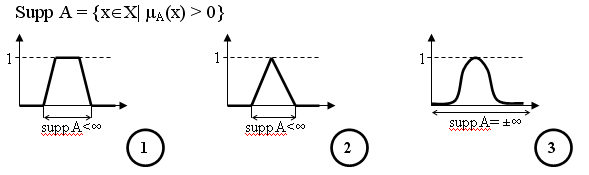
Если SuupA<∞, то основание называется компактным (совокупность точек является замкнутом и ограниченным)

Если SuupA=±∞, то основание называется некомпактным

2. Высота нечеткого множества – это точная верхняя грань функции принадлежности

Если hghA=1, то это нормализованное (нормальное) множество.

Если hghA<1, то это субнормализованное множество.

- коэффициент нормирования

3. -срез

 cut А = {xX , µ_A }

-срез – множество элементов х, для которых принимает значения не меньше заданного числа (0≤≤1).

4. Ядро

core A = {x  X | µ_A(x)=1}

*7. Основные свойства нечетких множеств. Нечеткое число и нечеткий интервал.[2/3]

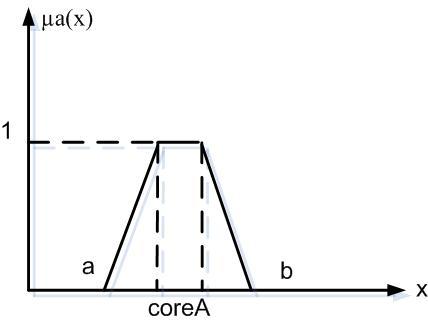
5. Точка перхода

сrossover_point = {xX | µ_A=0,5}

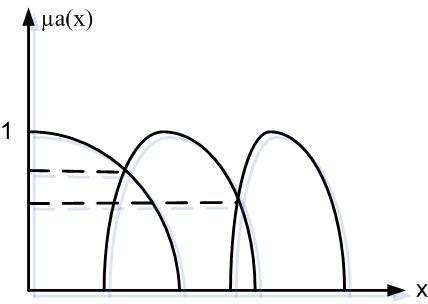
6. Выпуклые нечеткие множества. Нечеткое множество называется выпуклой, если выполняется следующее условие:

 x₁, x₂, x₃  Х : x₁  x₂  x₃ µ_A(x) min {µ_A(x₁); µ_A(x₃)}.

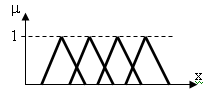
7. Нечеткое разбиение нечеткого множества А на нечеткие подмножества А_j:

Если А_j, j=1..N, hgh A_j = 1, A_j – выпуклое и для любого j А_j содержит не более 2-х пересечений с другими нечеткими подмножествами, то {A_j} – нечеткое разбиение.

*7. Основные свойства нечетких множеств. Нечеткое число и нечеткий интервал.[3/3]

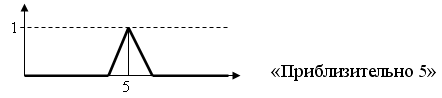
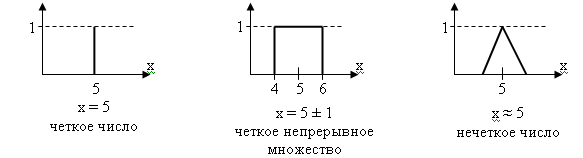
8. Нечеткое число.

Задается следующим образом: если для нечеткого множества задаются следующее условие: выпуклое, нормальное, кусочно-непрерывное, ядро А содержит одну точку

9. Нечеткий интервал.

Если выполняются условия 1, 2, 3, но не выполняется условие 4.

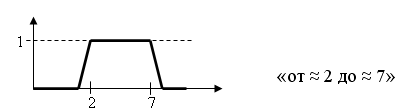
8. Понятия фаззификации, дефаззификации, лингвистической переменной. Пример. [1/1]

Определение операции фаззификации (fuzzification)

Определение: Процесс перехода от четкого представления к нечеткому называется фаззификацией.

Определение понятия лингвистическая переменная.

Определение: Переменная, значениями которой являются термы (слова, фразы на естественном языке) называется лингвистической.

Для проектирования нечеткой системы необходимо все переменные описать как лингвистические: задать для каждой переменной множество термов, а каждый терм описать как нечеткое множество со своей функцией принадлежности.

х – температура воды

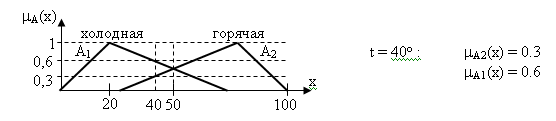
Таким образом, граница между нечеткими подмножествами является размытой и переход из одного подмножества в другое осуществляется плавно без скачков.