25. Преобразование алгоритма кластеризации с целью реализации в нейросетевом базисе. Структура сети Кохонена [1/1]

1. Количество входов – m, количество выходов – k. Выходы нейронной сети (НС) интерпретируется как вероятности принадлежности объектов к тому или иному классу. И ответом признается выход с максимальным значением.

2. Преобразуем следующий критерий , в нашем случае:.

.

Объект будет относиться к тому кластеру, у которого критерий (*) будет максимальным.

3. Реализация в нейросетевом базисе. Псевдокод для вычисления критерия (*).

цикл для p=1,n

цикл для l=1,k

(**)

конец цикла l

конец цикла p

При реализации в нейросетевом базисе: (**) – соответствует одному нейрону, цикл по l соответствует слою нейронов, для поиска l₀ – используется блок-интерпретатор, а цикл по p реализуется в процедуре обучения.

Примечание:

Каждый нейрон слоя

Коханена запоминает

с помощью своих

весовых коэф-тов

коэф-ты ядра кластера,

за который он отвечает

26. Алгоритм обучения без учителя для сетей Кохонена. Обобщенная процедура [1/1]

1. Инициализация весов

   1. малые случайные числа;

   2. равномерная инициализация;

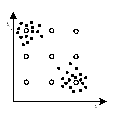
Для случая n=k обучение не проводится. Для нормальной работы n>>k.

1. специальные методы инициализации.

1. Обучающая выборка:

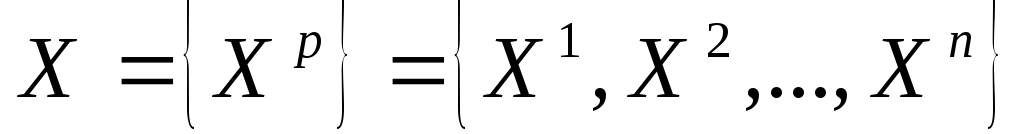
2. Рассчитывается l₀ – прямой проход по сети.

3. Корректировка весов сети Кохонена.

   1. традиционный способ;

Корректируются веса только нейрона победителя:

α – скорость обучения (0<α<1) монотонно убывает. Смысл корректировки весов заключается в попытке приблизить координаты нейрона – победителя к входному образу вектора. Обучение продолжается до тех пор пока координаты весов не перестанут изменяться. По окончанию обучения каждый нейрон отвечает за определение кластера.

2. метод выпуклой комбинации;

3. модифицированные алгоритмы.

27. Алгоритм обучения без учителя для сетей Кохонена. Метод выпуклой комбинации. Графическая интерпретация [1/1]

1. Инициализация весов

1. малые случайные числа;

2. равномерная инициализация;

3. специальные методы инициализации.

2. Обучающая выборка:

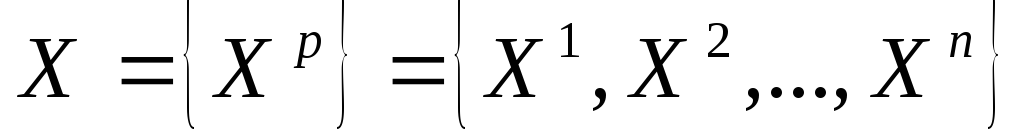
3. Рассчитывается l₀ – прямой проход по сети.

4. Корректировка весов сети Кохонена.

   1. традиционный способ;

2) метод выпуклой комбинации;

3) модифицированные алгоритмы.

Метод выпуклой комбинации:

1. Инициализация ядер кластеров производиться по правилу: i-му весу l-го ядра присваивается одинаковое значение.

, гдеn – количество векторов (объектов)

2. Множество X модифицируется в другое множество X_mod .

X→ X_mod

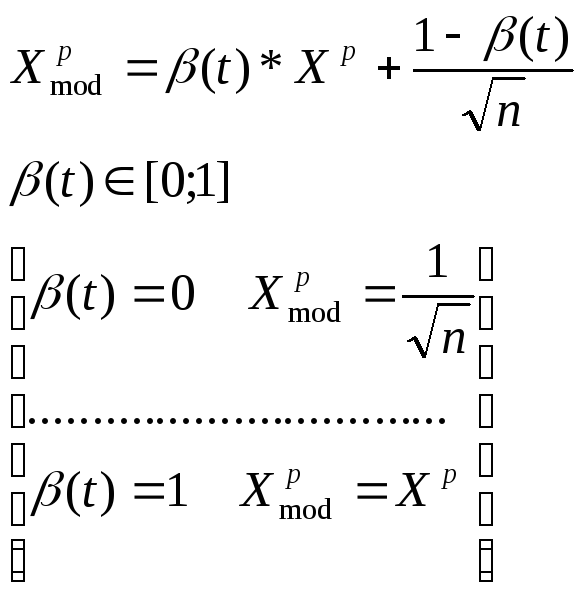
В процессе обучения обучающие вектора расходятся от значения к своим истинным значениям. При этом особенность обучения заключается в следующем: в процессе движения к своим истинным значениям обучающие вектора захватывают ядра кластеров пропорционально своей плотности распределения, а далее каждое ядро кластеров отслеживает движение обучающих векторов по мере роста .Графическая интерпретация:

28. Самоорганизующиеся карты (сок) Кохонена. Особенности обучения сок. Построение карт [1/1]

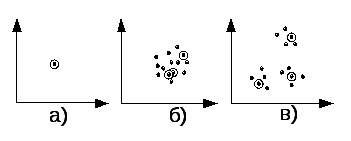
Построение карт введется по результатам работы сети Кохонена. СОК – это самоорганизующаяся структура, которая представлена в виде двухмерной сетки (т.е. решетки), в узлах которой находятся нейроны. Для построения СОК, обучение сети Кохонена ведется с учетом следующих особенностей:

1. Модификации подвергаются веса не только нейрона победителя, но его соседей.

m-мерное пространство, R-радиус

На первых шагах R-большое, далее снижается до 0.

Обучение производиться по следующей формуле: ,где - функция соседства нейронов,

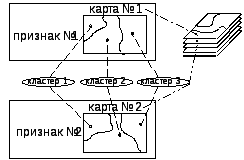
2. Построение карты ведется путем решения проблемы проецирования матрицы расстояний между нейронами на плоскость, при этом часто используется метод главных компонент.

Карта – это проекция матрицы расстояний между нейронами на плоскость с ее окраской по одному из признаков вектора X при этом интенсивность цвета окраски этой карты соответствует изменениям этого признака в заданном диапазоне. Этому диапазону ставиться весь спектр цветов (от синего до красного). Таких карт может быть построено столько, сколько признаков имеет входной вектор X (равно m). Положение объектов на каждой карте строго фиксировано.Анализ карт позволяет дать быструю качественную характеристику кластерам, т.е. выявить правила классификации.