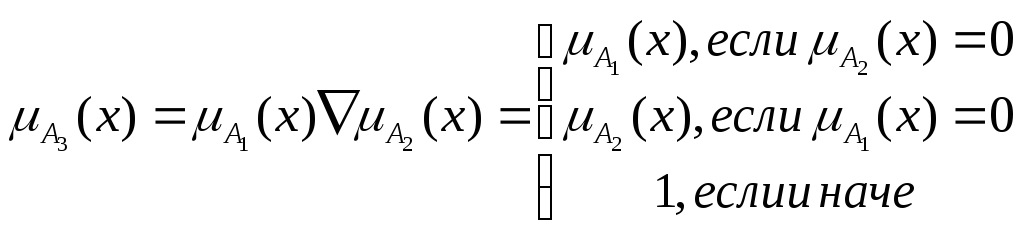- •1. Определение ии. Определение слабоформализуемых задач и их примеры. Определение сложных систем.[1/1]
- •2. История развития исследований в области ии.[1/1]
- •3. Основные свойства естественного интеллекта (еи).[1/1]
- •4. Основные направления исследований в области ии. Две точки зрения на развитие сии. [1/1]
- •5. Нечеткая логика. Краткие исторические сведения. Аспекты неполноты информации [1/1]
- •6. Определения четких и нечетких множеств. Определение нечеткого множества. Функция принадлежности. Примеры нечетких дискретных и непрерывных множеств. [1/2]
- •7. Основные свойства нечетких множеств. Нечеткое число и нечеткий интервал.[1/3]
- •*7. Основные свойства нечетких множеств. Нечеткое число и нечеткий интервал.[2/3]
- •*7. Основные свойства нечетких множеств. Нечеткое число и нечеткий интервал.[3/3]
- •8. Понятия фаззификации, дефаззификации, лингвистической переменной. Пример. [1/1]
- •9. Операции с нечеткими множествами (эквивалентность, включение, нечеткая операция «и», «или», «не»). [1/2]
- •10.Обобщение операций пересечения и объединения в классе т-норм и s-конорм[1/2].
- •11. Нечеткие отношения. Композиционные правила (max-min) и (max-prod). Примеры. [1/1]
- •12. Нечеткие алгоритмы. Обобщенная схема процедуры нечеткого логического вывода. [1/2]
- •13. Нечеткие алгоритмы. Метод максимума-минимума (метод Мамдани) как метод нечеткого логического вывода (изложение необходимо сопроводить примером). [1/2]
- •14. Нечеткие алгоритмы. Метод максимума-произведения (метод Ларсена) как метод нечеткого логического вывода (изложение необходимо сопроводить примером)[1/1].
- •15.Методы дефаззификации[1/1].
- •16.Процедура (схема) нечеткого логического вывода. Пример нечеткого логического вывода для выполнения нескольких правил. Достоинства и недостатки систем, основанных на нечеткой логике[1/2].
- •17.Искусственные нейронные сети. Особенности биологического нейрона. Модель искусственного нейрона [1/2].
- •18.Определение искусственной нейронной сети (инс). Однослойный и многослойный персептроны [1/1].
- •19. Классификация инс. Задачи, решаемые с помощью нейронных сетей [1/2].
- •20.Основные этапы нейросетевого анализа. Классификация известных нейросетевых структур по типу связей и типу обучения и их применение [1/1].
- •21. Алгоритм обучения с учителем для многослойного персептрона [1/1]
- •22. Алгоритмы обучения нейронных сетей. Алгоритм обратного распространения ошибки [1/1]
- •23. Проблемы обучения нс[1/1].
- •24. Сети Кохонена. Постановка задачи кластеризации. Алгоритм кластеризации[1/1].
- •25. Преобразование алгоритма кластеризации с целью реализации в нейросетевом базисе. Структура сети Кохонена [1/1]
- •26. Алгоритм обучения без учителя для сетей Кохонена. Обобщенная процедура [1/1]
- •27. Алгоритм обучения без учителя для сетей Кохонена. Метод выпуклой комбинации. Графическая интерпретация [1/1]
- •28. Самоорганизующиеся карты (сок) Кохонена. Особенности обучения сок. Построение карт [1/1]
- •29. Проблемы обучения инс [1/1]
- •30. Генетические алгоритмы. Определение. Назначение. Сущность естественного отбора в природе [1/1]
- •31. Основные понятия генетических алгоритмов [1/1]
- •32. Блок-схема классического генетического алгоритма. Особенности инициализации. Пример. [1/1]
- •33. Блок-схема классического генетического алгоритма. Селекция хромосом. Метод рулетки. Пример.[1/2]
- •33. Блок-схема классического генетического алгоритма. Селекция хромосом. Метод рулетки. Пример.[2/2]
- •34. Блок-схема классического генетического алгоритма. Применение генетических операторов. Пример.[1/1]
- •35. Блок-схема классического генетического алгоритма. Проверка условия остановки га.[1/1]
- •36. Достоинства генетических алгоритмов.[1/1]
- •37. Гибридные сии и их виды.[1/2]
- •38. Структура мягкой экспертной системы.[1/1]
- •39.Методология разработки интеллектуальных систем. Виды прототипов экспертных систем.[1/1]
- •40.Обобщенная структура основных этапов разработки экспертных систем.[1/2]
- •1. Идентификация.
- •2. Концептуализация.
- •3. Формализация
- •4. Программирование.
- •5. Тестирование на полноту и целостность
9. Операции с нечеткими множествами (эквивалентность, включение, нечеткая операция «и», «или», «не»). [1/2]
1. Операция эквивалентности
![]()
![]()
2. Операция включения
![]()
3. Нечеткая операция «НЕ» (дополнение)
|
|
|
4. Нечеткая операция «И»
а) логическое произведение (Заде)
|
|
|
б) алгебраическое произведение (Бандлер, Коходт)
|
|
|
в) граничное произведение (Лукасевич, Гринс)
|
|
|
г) драстическое произведение (Вебер)
|
|
|
*9. Операции с нечеткими множествами (эквивалентность, включение, нечеткая операция «И», «ИЛИ», «НЕ»). [2/2]
5. Нечеткая операция «ИЛИ»
а) логическая сумма (Заде)
|
|
|
б) алгебраическая сумма
|
|
|
в) граничная сумма
|
|
|
г) драстическая сумма
|
|
|
10.Обобщение операций пересечения и объединения в классе т-норм и s-конорм[1/2].
Один из подходов к обобщению операторов пересечения и объединения заключается в классе треугольных норм Т-норм и S-конорм.
Т-норма – операция пересечения.
S-конормы – операция объединения.
Т-нормы и S-конормы обладают следующими св-ми:
1) T(x,y) и S(x,y) – это функции двух переменных, область определения которых 0≤x≤1, 0≤y≤1, а область значений 0≤ T(x,y)≤1, 0≤ S(x,y)≤1:
T:[0,1]x[0,1]→[0,1]; S:[0,1]x[0,1]→[0,1].
2) Коммутативность. T(x,y)=T(y,x); S(x,y)=S(y,x).
3) Ассоциативность. T[T(x,y),z]=T[x,T(y,z)]; S[S(x,y),z]=S[x,S(y,z)].
4) Монотонность. T(x,y)= T(u,v), x=u, y=v; S(x,y)= S(u,v), x=u, y=v.
5) Ограниченность. T[0,y]=0; T[1,y]=y; S[0,y]=y; S[1,y]=1.
T(x,y) и S(x,y) называются триангулярными (треугольными) функциями, т.к. они определяются в треугольной области.
|
Т-норма: T(x,y). «И» |
S-конорма: S(x,y). «ИЛИ» |
|
1. Логическое произведение Tmin(x,y)=min{x,y}; Tmin(x1,x2,...,xn)=min{x1,x2,...,xn} |
1. Логическая сумма Smax(x,y)=max{x,y}; Smax(x1,x2,...,xn)=max{x1,x2,...,xn} |
|
2. Алгебраическое произведение Tprod(x,y)=x∙y; Tprod(x1,x2,...,xn)= |
2. Алгебраическая сумма Ssum(x,y)=x+y-x∙y; Ssum(x1,x2,...,xn)= |
|
3. Граничное произведение Tmax(x,y)=max(0;x+y-1); Tmax(x1,x2,...,xN)=
= |
3. Граничная сумма Smin(x,y)=min(1;x+y); Smin(x1,x2,...,xn)= |
|
4.
Драстическое произведение
|
4.
Драстическая сумма
|
Для любых заданных значений x,y справедливо:
0 ≤ T(x,y) ≤ T(1,y) ≤ y ≤ S(0,y) ≤ S(x,y) ≤ 1.
*10.Обобщение операций пересечения и объединения в классе Т-норм и S-конорм [2/2].
0 ≤ драстическое произведение (x,y) ≤ граничное произведение (x,y) ≤ алгебраическое произведение (x,y) ≤ логическое произведение (x,y) ≤ логическая сумма (x,y) ≤ алгебраическая сумма (x,y) ≤ граничная сумма (x,y) ≤ драстическая сумма (x,y) ≤ 1.
Пр. μA(x)=0,5 ; μB(x)=0,1.
«И»:
1) Tmin(μA(x); μB(x))=min((μA(x); μB(x)))= min(0,5; 0,1)=0,1;
2) Tprod(μA(x); μB(x))= μA(x)∙μB(x)=0,5*0,1=0,05;
3) Tmax(μA(x); μB(x))=max(0; μA(x) + μB(x) –1)=max(0; 0,5+0,1–1)=0;
4) TμA(x)∆μB(x)=0, т.к. max(μA(x); μB(x))=max(0,5; 0,1)=0,5<1.
«ИЛИ»:
1) Smax(μA(x); μB(x))=max((μA(x); μB(x)))= max(0,5; 0,1)=0,5;
2) Tsum(μA(x); μB(x))= μA(x)+μB(x) – μA(x)∙μB(x)= 0,5+0,1 – 0,5*0,1=0,55;
3) Tmin(μA(x); μB(x))=min(1; μA(x)+ μB(x))=min(1; 0,5+0,1)=0,6;
4) TμA(x)▼μB(x)=1, т.к. min(μA(x); μB(x))=min(0,5; 0,1)=0,1>0.