1.3.1. Скорость газа и диаметр абсорбера

Скорость газа в интервале устойчивой работы провальных тарелок может быть определена с помощью уравнения (1.3):

(1.32)

Здесь:

где w – скорость газа в колонне, м/с; – эквивалентный диаметр отверстия или щели в тарелке, м; – доля свободного сечения тарелки, м²/м²; , – вязкость соответственно поглотительного масла при температуре в абсорбере и воды при температуре 20 °С, Па · с.

Подставив численные значения, получим:

Коэффициент В равен 2,95 для нижнего и 10 – для верхнего пределов нормальной работы тарелки. Наиболее интенсивный режим работы тарелок соответствует верхнему пределу, когда В = 10, однако с учетом возможного колебания нагрузок по газу принимают В = 6–8.

Приняв коэффициент B = 8, получим:

По каталогу [12] (см. прил. 5.1) выберем решетчатую провальную тарелку со свободным сечением F_c = 0,2 м²/м² и шириной щели у = 6 мм; при этом = 2 у = 2 · 0,006 = 0,012 м.

Тогда:

Отсюда: w = 2,74 м/с.

Для ситчатых тарелок рабочую скорость газа можно рассчитать по уравнению [7]:

(1.33)

Для клапанных тарелок:

(1.34)

где G – масса клапана, кг; S₀ – площадь отверстия под клапаном, м²; – коэффициент сопротивления, который может быть принят равным 3.

По ГОСТ 16452–79 диаметр отверстия под клапаном равен 40 мм, масса клапана – 0,04 кг.

Для колпачковых тарелок предельно допустимую скорость рекомендуется рассчитывать по уравнению [1]:

(1.35)

где – диаметр колпачка, м; – расстояние от верхнего края колпачка до вышерасположенной тарелки, м.

Диаметр абсорбера находят из уравнения расхода (1.10):

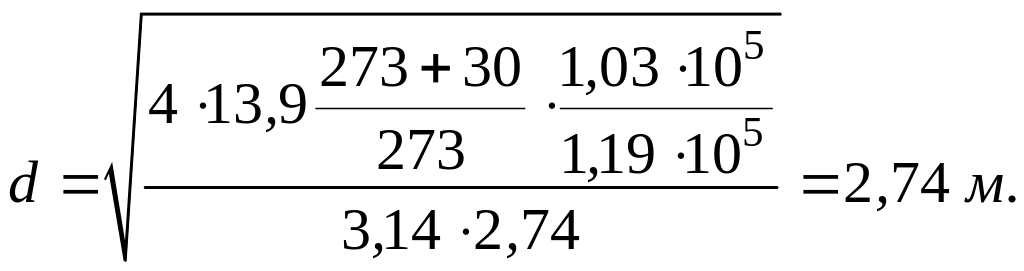
Принимаем [6] стандартный диаметр обечайки абсорбера d = 2,6. При этом действительная скорость газа в колонне:

1.3.2. Коэффициент массопередачи

Обычно расчеты тарельчатых абсорберов проводят по модифицированному уравнению массопередачи, в котором коэффициенты массопередачи для жидкой и газовой фаз относят к единице рабочей площади тарелки:

(1.36)

где М – масса передаваемого через поверхность в единицу времени массопередачи вещества, кг/с; F – суммарная рабочая площадь тарелок в абсорбере, м².

Необходимое число тарелок F определяют делением суммарной площади тарелок F на рабочую площадь одной тарелки f

(1.37)

Коэффициенты массопередачи определяют по уравнениям аддитивности фазовых диффузионных сопротивлений:

(1.38)

где и – коэффициенты массоотдачи, отнесенные к единице рабочей площади тарелки соответственно для жидкой и газовой фаз, кг/(м²·с).

В литературе приводится ряд зависимостей для определения коэффициентов массоотдачи. На основании сопоставительных расчетов рекомендуем использовать обобщенное критериальное уравнение [13], применимое для различных конструкций барботажных тарелок:

(1.39)

При этом для жидкой фазы:

для газовой фазы:

где А – коэффициент; , – коэффициенты молекулярной диффузии распределяемого компонента соответственно в жидкости и газе, м²/с; – средние скорости жидкости и газа в барботажном слое, м/с; – газосодержание барботажного слоя, м³/м³; – критерий гидравлического сопротивления, характеризующий относительную величину удельной поверхности массопередачи на тарелке; – гидравлическое сопротивление барботажного газожидкостного слоя (пены) на тарелке, Па; – высота слоя светлой (неаэрированной) жидкости на тарелке, м; l – характерный линейный размер, равный среднему диаметру пузырька или газовой струи в барботажном слое, м.

В интенсивных гидродинамических режимах характерный линейный размер становится, по данным ряда авторов [13], практически постоянной величиной, мало зависящей от скоростей фаз и их физических свойств. В этом случае критериальные уравнения, решенные относительно коэффициентов массоотдачи, приводятся к удобному для расчетов виду:

(1.40)

(1.41)