3.3. Відношення, пропорції, сумірність

Важливою умовою цілісності і завершеності архітектурного твору є сумірність і субординація всіх елементів, тобто узгодженість частин і цілого. Число, відповідність, відношення з давніх часів використовуються у формоутворенні як засоби досягнення гармонії.

Гармонія (грец. harmonia) – сумірність, співзвучність, зв'язок. Суттю архітектурної гармонії є пропорційність частин і елементів та їх сумірність архітектурному цілому. Гармонія в архітектурі – впорядкована різноманітність, взаємовідповідність окремих складових архітектурної форми, що обумовлюють її якісну визначеність та цілісність (А. Мардер, 1995).

Всі гармонійні відношення поділяють на дві великі групи: раціональні (прості) та ірраціональні (пропорції). Зведені у пропорційну систему ці відношення стають засобом архітектурної композиції.

В літературі поняття пропорції часто ототожнюється з відношенням. Відношення в архітектурі характеризують геометричну форму і більшою мірою пов’язані з функціонально-технічними питаннями. Наприклад, розміри будинків – це об’єктивна реальність, але відношення цих розмірів самі по собі не створюють естетичної цінності. Досягається архітектурна гармонія в результаті встановлення певних співвідношень між величинами, які викликають ті чи інші естетичні емоції: легкість, масивність, напруженість тощо. Пропорції служать засобом впорядкування і встановлення закономірних взаємозв’язків між усіма частинами споруди. Рівність відношень (пропорційність) габаритів геометричних форм використовується для встановлення сумірних відношень частин і цілого в архітектурі, для досягнення гармонії.

Сумірність і пропорція – дві категорії естетики, понятійна границя між якими не є чіткою. Сумірність – це співвідношення розмірів форми за трьома координатами простору (довжина, ширина, висота), яка визначає об’єкт або будь-яку його складову частину, структурно визначену, з чіткими границями, як ціле. Наприклад, можемо говорити про сумірність тіла людини або його частин – голови, стопи, пальця чи навіть фаланги пальця. Це характеристика без розмірів, яка не має розмірного модуля і утворюється в результаті порівняння висоти, ширини і довжини. Пропорція – поняття широке і складне. В галузі архітектури і мистецтва воно має конкретне значення: пропорція – це зв'язок, яким з’єднані всередині складного цілого складові частини, це рух від розміру до розміру, який об’єднує сумірності і будує ритми членувань (І. Шевельов).

Пропорція виявляє структурну єдність цілого, в той час як сумірність відтворює образ, який асоціюється з уявою про якість (сила і слабкість, стійкість, гнучкість, міцність тощо).

3.3.1. Види відношень. Раціональні (прості) відношення та раціональна пропорційна система. Модуль як основа раціональної пропорційної системи. Просторова система модульних координат.

Відношення можуть виражатися раціональними або ірраціональними числами.

Раціональними числами є числа, які можна записати у вигляді дробу а/b, де а і b – цілі числа (b≠0); такий дріб називається простим дробом або простим відношенням.

Число, яке можна виразити у вигляді безкінечного десяткового неперіодичного дробу, називається ірраціональним, відповідно відношення чисел – ірраціональним відношенням

Геометричний вигляд форми, який є результатом співвідношень величин форми за трьома координатами простору і визначає її як лінійну, площинну й об'ємну, може виражатися кількісно у вигляді числових відношень її параметрів. Співвідношення 1:1 визначає форму квадрата, 3 : 2 – прямокутника, постійність радіусу r = const в тілах обертання характеризує кулю тощо.

Архітектор завжди має справу з відношеннями параметрів форми. Відношення дають уявлення про форму та її функціональні якості. Так, розмір висоти приміщення, наприклад, 3 м не дозволяє охарактеризувати геометричну форму приміщення. Якщо додати, що ширина приміщення 50 м, а довжина 30 м, легко уявити геометричну форму цього приміщення з низькою нависаючою стелею.

Таким чином, в архітектурі порівняння геометричних параметрів відтворюється за допомогою відношень.

Раціональним або простим відношенням в архітектурі називають таке відношення, в якому залежність двох величин відтворюється простим дробом, де чисельник і знаменник – цілі числа від 1 до 7 ± 2 (умовно, до межі ясного бачення сумірностей величин, які сприймаються людиною).

Одним з найпростіших числових прийомів узгодження частин і цілого у сучасному проектуванні є використання модуля, модульної сітки. Принцип числового взаємозв’язку частин і цілого був закладений вже у єгипетському каноні, який використовувався для ліплення статуй. Висота фігури дорівнювала 19 частинам. Умовною одиницею вимірювання частин, модулем служила довжина середнього пальця. Числа 3, 4, 5 – сторони «священного» трикутника, за допомогою якого єгиптяни будували прямий кут і правильні прямокутники. Система модульних пропорцій на основі єгипетського трикутника наведена в параграфі 4.4.

На відношенні 1 : 1 будуються найпростіші геометричні форми – квадрат і куб. Кратні відношення – 1 : 2, 1 : 3, 1 : 4, 1 : 5… – дають в прямокутній формі повторення квадрата ціле число раз, менша величина – квадрат – служить модулем, одиницею виміру більшої величини.

Прості відношення 2 : 3, 3 : 4, 2 : 5, 5 : 6 містять в собі модуль, який укладається цілу і невелику кількість раз в кожній просторовій величині, яка входить у співвідношення.

На основі простих кратних цілочислових відношень заснована раціональна пропорційна система. В її основі лежить модуль, який може виражатися у фізичних розмірах будь-якого елемента або в абсолютних розмірах. У давнину (крім фізичних розмірів частин тіла людини) як відносне числове значення модуля вибирався розмір одного з елементів конструкцій. Наприклад, в античних ордерних системах модулем був радіус (діаметр) нижньої частини колони; у давньоруських храмах – товщина стіни, сторона підкупольного квадрата. Розміри трьох ребер цегли (найдавнішого будівельного матеріалу), як правило роблять кратними, наприклад, стандартна цегла має розміри 65 : 120 : 250, а з урахуванням швів вони співвідносяться, як 1 : 2 : 4. Це дає можливість створювати різноманітні конструктивні види кладок.

Модуль (від лат. modulus – міра) – в архітектурі і будівництві умовна одиниця виміру, прийнята для визначення кратних співвідношень розмірів частин будинку, усього будинку або комплексу будинків, а також конструкцій і виробів. Впровадження метричної системи мір привело до прийняття абсолютного числового значення модуля. У більшості країн – 100 мм. На його основі встановлюються похідні модулі n х М, в т. ч. укрупнені (n > 1) і дробові (n < 1). Модуль і модульна координація розмірів є основою уніфікації й відіграють певну естетичну роль (В. Дахно, 1995). Розміри і розташування будинків та їх елементів можуть визначатися за допомогою просторової системи модульних координат. Проекція просторової системи на площину утворює модульну планувальну сітку.

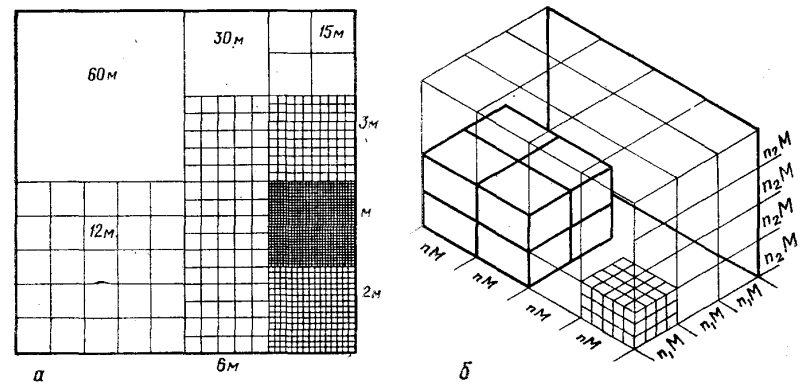
Рисунок 21 - Модульна система

а) модульна планувальна сітка (сітка єдиного ряду будівельних модулів).

б) просторова система модульних координат.

Модульне проектування в архітектурі є одним з ефективних способів формоутворення. Детальніше про використання модуля – у розділі «Комбінаторика».

Результатом раціональних відношень є подібність елемента цілому. Подібні форми полегшують завдання приведення різних просторових елементів до єдності. Принцип подібності елемента цілому є особливим засобом організації цілісної форми.

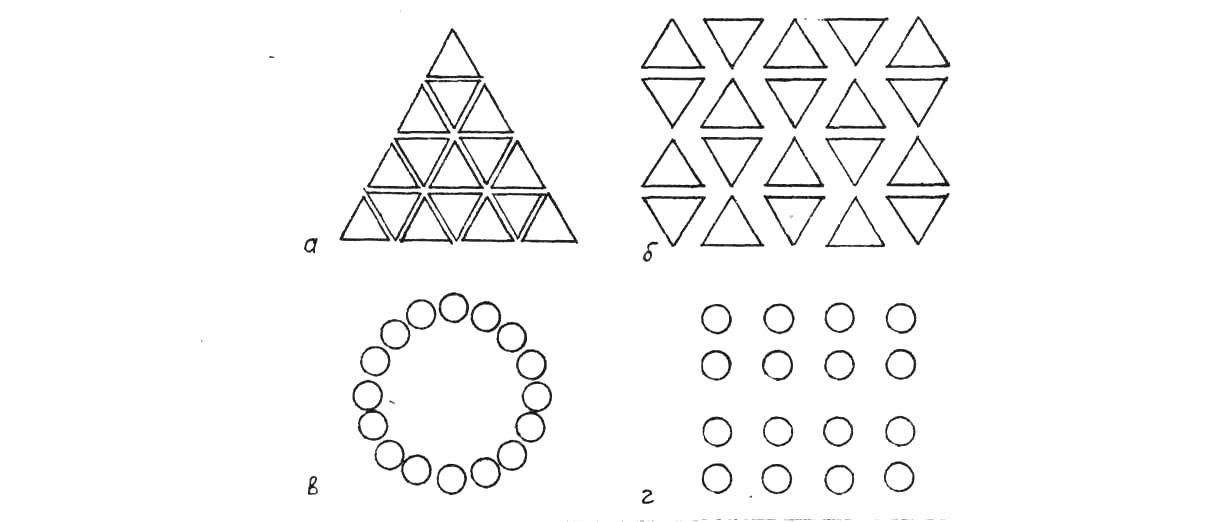
Рисунок 22 - Подібність елемента цілому забезпечує єдність форми і використовується як засіб її організації: а), в) яскраво виражена єдність елементів; б), г) стійкість системи знижена.

Подібність елементів особливо ефективна у формах, що складаються з числа елементів менше (72). При кількості елементів більше ніж (72) закономірність подібності може виражатися рядами.

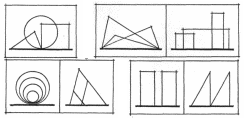
а, б

в, г

Рисунок 23 - Різні прояви подібності: а) неподібні форми; б) форми з неповною (афінною) подібністю; в) подібні форми; г) абсолютна подібність

3.3.2. Ірраціональні відношення (пропорції). Арифметична, геометрична і гармонійна прогресії. Середні числа. Гармонійні пропорції. Геометричні способи побудови рядів на основі геометричної пропорції, «золотого перерізу», співвідношення сторони і діагоналі квадрата (система вписаних квадратів та система прямокутників – похідних квадрата)

Пропорція (від латинського ргорогtіо – співвідношення, розмірність) – співвідношення частин і цілого між собою. В античності поняття «пропорція» було аналогічним поняттям «відповідність», «схожість», «подібність».

Понят­тя співвідношення в архітектурі вбирає в себе увесь спектр взаємо­зв'язків, величин, що характеризують об'єктивні властивості фор­ми. Таким чином, пропорція фіксує однорідність (закономірність) змін кількісної міри при переході від однієї частини форми до іншої. Пропорції – це рівність відношень кількісної міри однакових об’єктивних якостей у формах, що зіставляються між собою (А. Тіц, 1976).

Пропорції, ірраціональні відношення або відношення дробових чисел, будуються за допомогою простої геометричної побудови.

Використання пропорцій – один з основних прин­ципів гармонійної організації цілого. Однак математична точність сама по собі не визначає гармонії при створенні якогось твору. Математичний метод дає лише кількісне поняття і знання існуючих пропорційних закономірностей.

Вивченням пропорційних залежностей у XX столітті займалися такі відомі діячі, як американський мистецтвознавець Д. Хембридж, французький архітектор Ле Корбюзье, радянські академік архітектури І.В. Жолтовський, доктор мистецтвознавства професор О.А. Тіц, український вчений Тищенко та ін., що зробили істотні внески в теоретичні системи пропорцій.

Принцип рівної зміни як засіб конструювання архітектурної форми добре відомий у практиці та теорії архітектури і мистецтва. Це арифметична прогресія, гармонійна прогресія, геометрична прогресія. Першій з них близькі кратні модульні системи, другу покладено в основу музичної будови, третя – пропорція в її математичному значенні.

Арифметична прогресія – це послідовність чисел, в якій кожне наступне число більше ніж попереднє на одну й ту саму величину. Будь яка мірна стрічка є взірцем арифметичної прогресії. Принцип арифметичної прогресії дозволяє знаходити середні відношення: кожний член арифметичної прогресії є середнім арифметичним двох суміжних членів. Якщо взяти, наприклад, ряд 1, 4, 7, 10, 13, 16 і т.д., то кожний його член – середнє двох суміжних: (7+13)/2= 10. Якщо, наприклад, висота приміщення 4м, а глибина 10м, то легко визначити за середньоарифметичним його ширину; вона дорівнює (4+10)/2= 7.

Гармонійна прогресія – ланцюг величин, в якій послідовність чисел, зворотних даним, утворює арифметичну прогресію. Будь який член такої прогресії є середнім гармонійним сусідніх членів. Ряд 1/2, 1/3, 1/4, 1/5, 1/6 є гармонійна прогресія, тому що зворотне число будь якого члена ряду є середнім арифметичним чисел, зворотних сусіднім числам ряду: 3/4=(2+4)/2 і т.д. Піфагор був першим, хто помітив, що висота тону струни зворотно пропорційна довжині натягнутої струни. Якщо смикнути натягнуту струну, а потім притиснути пальцем середину і знову смикнути, то тон, який видасть струна, буде на октаву вищим, ніж у першому випадку. Якщо притиснути струну і заставити її коливатись тільки на третині її довжини, то частота тону буде втричі вищою основної частоти. Притискаючи струну в точках, віддалених від кінця на раціональне кратне довжини, отримуємо всю гаму.

Послідовність чисел, яка утворює ряд геометричної прогресії, визначається тим, що кожне наступне число більше попереднього в одне ї те саме число раз. Наприклад, ряд 1, 3, 9, 27, 81 – геометрична прогресія з множником 3. Кожний член гео­метричної прогресії дорівнює коре­ню квадратному з добутку попереднього і наступного членів ряду і є середнім гео­метричним.

Середні числа – числа арифметичного, гармонійного і геометричного рядів слугували засобом досягнення гармонійних розмірно-просторових структур. Архітектори і скульптори були переконані, що те, що добре для слуху не може бути поганим для зору. Палладіо користувався середніми числами наступним чином. Приміщення з плоскими перекриттями визначались ним в розрізі відношенням 1:1, сумірності склепінчастих приміщень визначались на середньоарифметичних або середньогеометричних числах. Дюрер користувався і арифметичною і геометричною шкалами пропорцій.

Серед різноманітних середніх відношень найбільшої уваги заслуговує відношення золотого перерізу – середнє геометричне, яке володіє низкою математичних властивостей, які дивовижним чином зійшлися у ньому. Це відношення виявляється при розгляді різноманітних явищ природи, і в першу чергу – явищ, пов’язаних з органічним ростом. І до цього часу це відношення залишається загадкою. Золотий переріз відтворюється зазвичай або як 0,618, або 1,618. Це зворотні числа: позначивши 1,618 через Ф, маємо 1/Ф = 0,618. Якщо помножити послідовно 1 на Ф, потім знову на Ф і т.д., знаходять зростаючий ряд золотого перерізу, а множачи послідовно на 1/Ф, знаходять убуваючий ряд. Легко помітити, що в цьому ряді 0,146 – 0,236 – 0382 – 0,618 – 1 – 1,618 – 2,618 – 4,236 – 6,854 кожне число не тільки результат множення попереднього на число Ф, але дорівнює також сумі двох попередніх. Для тріади золотого перерізу Ф1 – Ф2 – Ф3 = 1 – 1,618 – 2,618 характерно не тільки Ф1/Ф2 = Ф2/Ф3 і Ф3 = Ф1 + Ф2 = 2,618=1+1,618, але й Ф2² = Ф3= 1,618² = 2,618. Якщо Ф = 1,618, то можна записати 1 + Ф = Ф². Це рівняння має суттєве значення для з’ясування природи золотого перерізу.

У математичному вираженні пропорція – це рівність відношень а : в = с: d. Звичайна математична пропорція вимагає, щоб у рівність входили чотири члени. Геометричну пропорцію знаходять з трьох елементів: а : b = b : с. Для геометричної пропорції, що її називають «безупинною», характерна наявність загального члена b, який називається середньою пропорційною, або середньою геометричною величиною.

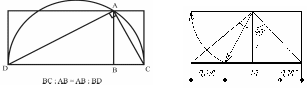
Рисунок 24 - Графічне вираження середньої пропорційної величини

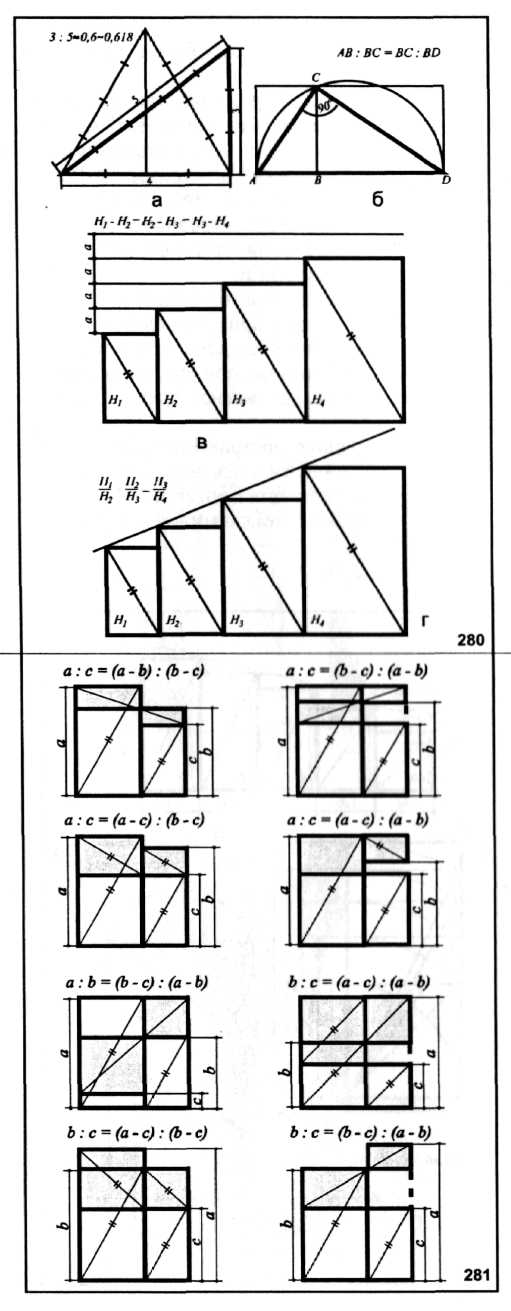
Рисунок 25 - Графічне вираження геометричної пропорційної залежності

Існують також пропорційні залежності що об'єднані загальною назвою гармонійні пропорції.

У III ст. до н.е. грецький математик Евклід розглядав вісім гармонійних пропорцій. У них таксамо, як і в геометричну, входять три елементи: а, b, с.

Рисунок 26 - Гармонійні пропорції за Евклідом

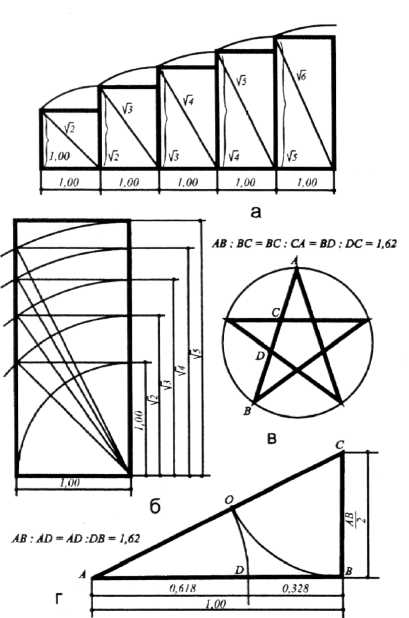
Рисунок 27 - Графічне вираження пропорційної залежності, побудованої на відношеннях сторін прямокутника, яку використовували в архітектурі Стародавньої Греції

Золотий переріз, який також є гармонійною пропорцією, на відміну від інших пропорцій утворюється при сполученні тільки двох величин: а і Ь. В математиці його формулюють таким чином: поділ цілого на дві нерівні частини пропорційний, коли менша частина цілого так відноситься до більшої, як більша частина до цілого (а – Ь) : Ь = Ь : а й обернено – ціле так відноситься до більшої частини, як більша до меншої, тобто: а : Ь = Ь : (а – Ь). Відношення між двома величинами постійне і виражається нескінченним десятковим дробом, де більший відрізок дорівнює 0,618, менший – 0,382.

Золотий переріз виражається також геометричним шляхом відповідних побудов.

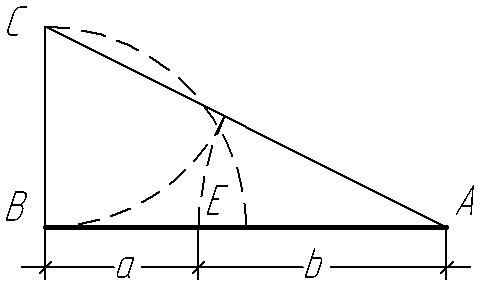
Рисунок 28 - Геометрична побудова золотого перерізу

Щоб розділити відрізок АВ у пропорції золотого перерізу, необхідно в точці В поставити перпендикуляр ВС, рівний половині АВ. Одержуємо прямокутний трикутник АВС із співвідношенням катетів 1 : 2. З вершини С радіусом СВ проводимо дугу на гіпотенузу СА; одержуємо точку О. Далі з вершини А радіусом АО проводимо дугу на основний відрізок АВ; одержуємо точку, яка поділяє даний відрізок у пропорції золотого перерізу. Відношення АД : ДВ = АВ : АД = 1,628.

Складна ірраціональна система відношень ще у середньовіччі була замінена близькими відношеннями простих чисел. На честь автора цільночислове вираження «золотого ряду» названо рядом Фібоначчі: 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144...

Ряд золотого перерізу виражається такими цифрами: 0,09; 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618 і т.д. Практично найчастіше застосовується досліджуваний у XII ст. відомим італійським математиком Фібоначі наближений золотий переріз, що виражений у цілих числах. Ця пропорційна залежність названа на честь автора «Ряд Фібоначі»: 1; 2; 3; 5; 8; 13; 21; 34; 55; 89 і т.д. Будь-який член ряду дорівнює сумі двох попередніх, аналогічних ряду золотого перерізу, при цьому співвідношення сусідніх членів наближається до золотого перерізу і наближення збільшується із зростанням ряду – 0, 618 (3:5 = 0, 6; 5:8 = 0,625; 8 : 13 = 0,615; 13:21 = 0,619; 21 : 34 = 0,617 і т.д.)

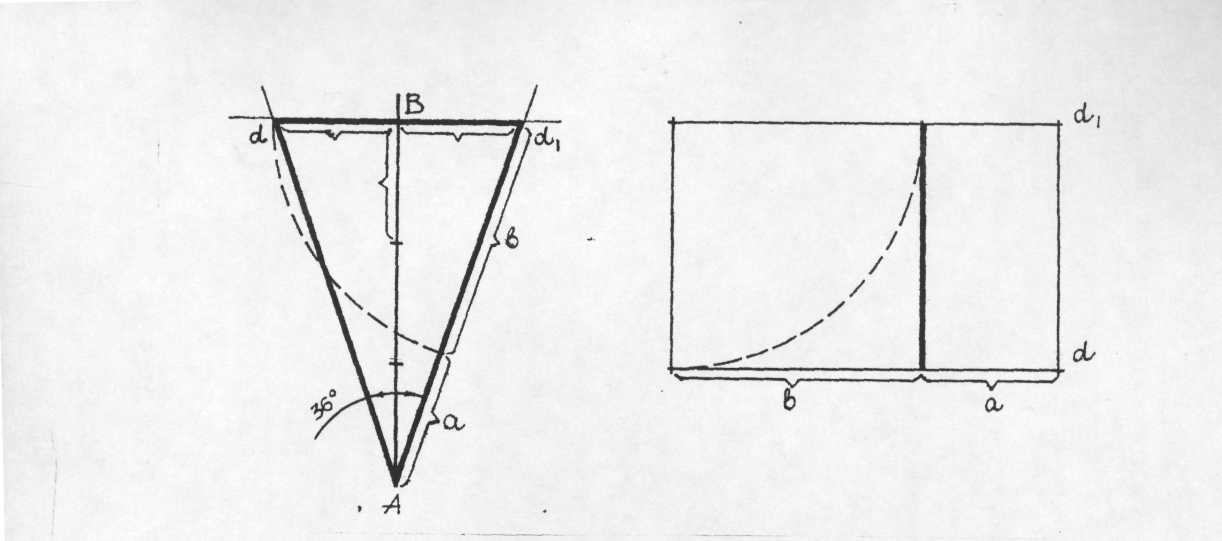
Рисунок 29 - Побудова «золотого трикутника» та «золотого прямокутника»

Серед інших гармонійні відношення, на основі яких будуються пропорційні системи (Рис. 30), наведені в параграфі 4.4.

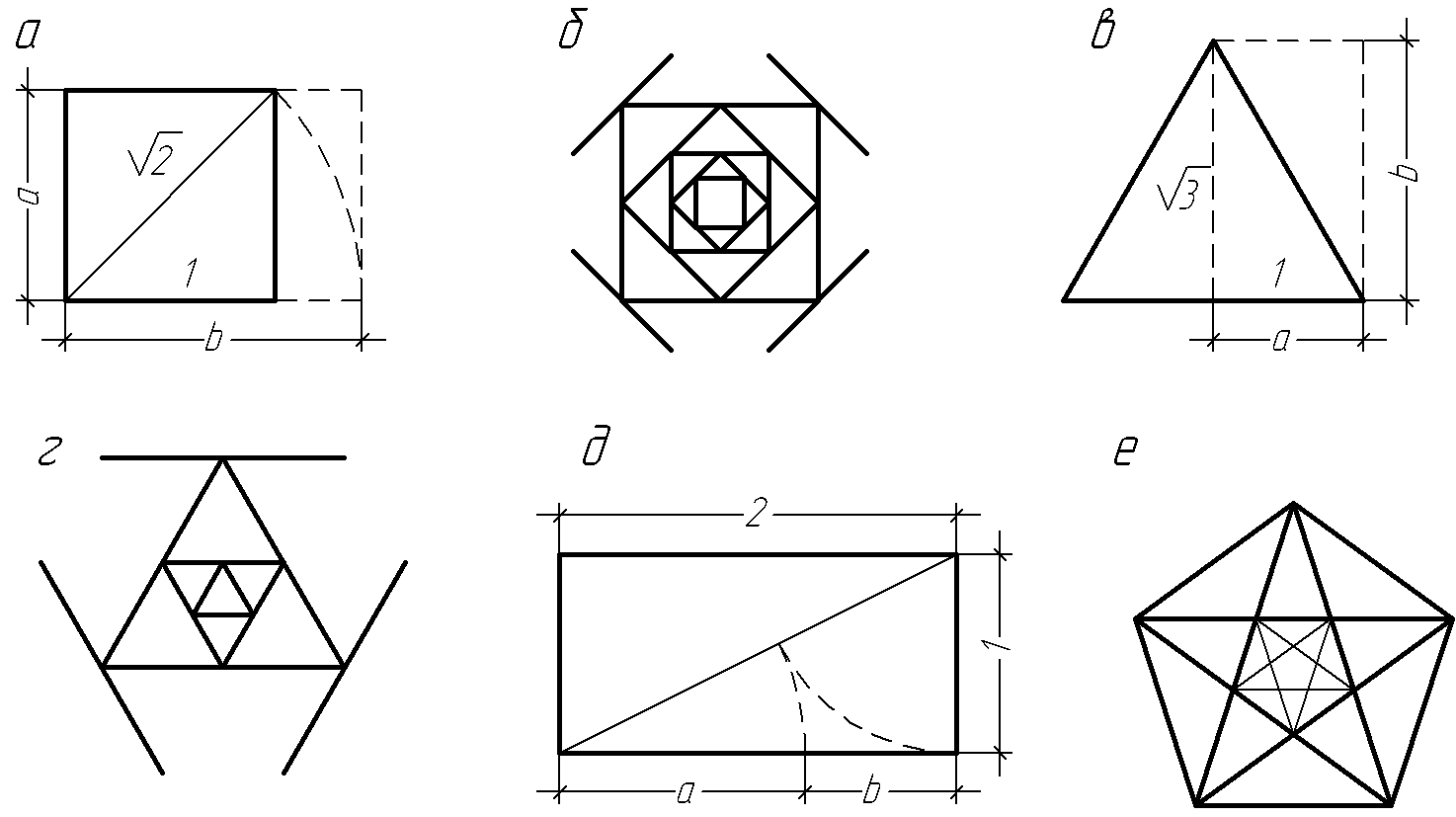
а б

Рисунок 30 - а) відношення сторони квадрата до його діагоналі: ;

б) відношення половини основи до висоти рівностороннього трикутника: .