
- •2) Определение линейной зависимости системы векторов линейного пространства
- •Размерность и базис линейного пространства, координаты вектора
- •Подпространство
- •[Править]Свойства подпространств
- •3) Базис линейного пространства
- •6) Линейные преобразования линейного пространства
- •7) Собственные значения и собственные векторы
- •Определение
- •Симметричные матрицы, статистики и моделирования
- •Собственные значения и собственные векторы симметричной матрицы
- •Собственные значения и собственные векторы симметричной матрицы реальные
- •Собственных векторов симметричной матрицы, ортогональны
- •Спектральное разложение симметричной матрицы
- •Проекция матрицы
- •Положительный (полу-) определенных матриц
1)
Определение линейного пространства
Пусть M —множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:
паре элементов множества
 отвечает
элемент
отвечает
элемент 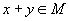 ,
называемый суммой x и y;
,
называемый суммой x и y;паре
 ,
,  —
любое действительное число, отвечает
элемент
—
любое действительное число, отвечает
элемент 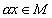 ,
называемый произведением числа
,
называемый произведением числа  и
элемента x.
и
элемента x.
Будем
называть множество M линейным
пространством, если
для всех его элементов определены
операции сложения и умножения на
действительное число и для любых
элементов ![]() и
произвольных чисел
и
произвольных чисел ![]() справедливо:
справедливо:
 ,
сложение коммутативно;
,
сложение коммутативно;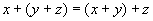 ,сложение
ассоциативно;
,сложение
ассоциативно;существует единственный нулевой элемент
 такой,
что
такой,
что 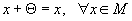 ;
;для каждого элемента существует единственный противоположный элемент -x такой, что
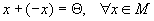 ,
, ,
умножение на число ассоциативно;
,
умножение на число ассоциативно;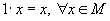 ;
;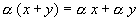 ,
умножение на число дистрибутивно
относительно сложения элементов;
,
умножение на число дистрибутивно
относительно сложения элементов;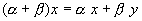 ,
умножение вектора на число дистрибутивно
относительно сложения чисел.
,
умножение вектора на число дистрибутивно
относительно сложения чисел.
Равенства 1—8 называют аксиомами линейного пространства.
Линейное пространство часто называют векторным пространством, а его элементы — векторами.
Некоторые свойства линейных пространств
Утверждение 1. В произвольном линейном пространстве нулевой элемент — единственный.
Утверждение 2. В произвольном линейном пространстве нулевой элемент равен произведению произвольного элемента на действительное число 0.
Оба утверждения доказаны на лекции.
Следующие 3 утверждения предложены в качестве упражнений к лекциям.
Утверждение 3. В произвольном линейном пространстве каждому элементу отвечает единственный противоположный элемент.
Утверждение 4. В произвольном линейном пространстве противоположный элемент произвольного элемента x равен произведению x на действительное число -1.
Утверждение 5. В произвольном линейном пространстве для любых двух произвольных элементов x и y существует и единственна разность: x-y = x+(-1) ·y.
Примеры линейных пространств
Пример 1. Нетрудно показать, что рассмотренное в п. 2.1. пространство арифметических векторов Rn является линейным пространством.
Пример 2. Рассмотрим множество M арифметических векторов из Rn, компоненты которых — целые числа.
Это множество не является линейным пространством.
Действительно, рассмотрим вектор x = (1, 1, …, 1) и действительное число a=0.5. Компоненты вектора x — целые числа, он принадлежит множеству M, но компоненты произведения ax = (0.5, 0.5, …, 0.5) не являются целыми числами, и, следовательно, ax не принадлежит множеству M.
Пример 3. Рассмотрим множество M n многочленов с действительными коэффициентами относительно одного переменного, n-й степени, n>1, с определенными для многочленов операциями сложения и умножения на число.
M n = {Pn| Pn (t) = antn + an-1t n-1 + … + a1t + a0, an не равно 0}
Это множество не является линейным пространством.
Действительно., рассмотрим Pn = t n + t и Qn = - t n. Оба эти многочлена принадлежат множеству. Однако их сумма, Pn + Qn = (t n + t) + (- t n) = -t,
Не принадлежит M n, поскольку -t — многочлен первой степени, а множество M n содержит многочлены n-й степени, n >1.
Пример 4. Рассмотрим множество M n многочленов с действительными коэффициентами относительно одного переменного, степени не выше n, n>1, с определенными для многочленов операциями сложения и умножения на число:
M n = {Pn| Pn (t) = antn + an-1t n-1 + … + a1t + a0},
В отличие от предыдущего примера не требуется, чтобы старший коэффициент был отличен от нуля.
Pn + Qn = Pn (t) + Qn (t) =
= (antn + an-1t n-1 + … + a1t + a0) + (bntn + bn-1t n-1 + … + b1t + b0)=
= (an+ bn)tn + (an-1+ bn-1)t n-1 + … + (a1+ b1)t +(a0+ b0),
?Pn = ?Pn (t) = ? (antn + an-1t n-1 + … + a1t + a0) = ?antn + ?an-1t n-1 + … + ?a1t + ?a0.
Это множество является линейным пространством.
Действительно.
Во-первых, при сложении многочленов и умножении многочлена на число получается многочлен, степень которого не выше n. Т.е. каждой паре многочленов из Mn соответствует их сумма — многочлен из Mn . Точно так же, произведением произвольного многочлена на действительное число является многочлен той же степени, т.е. каждому многочлену из Mnи каждому действительному числу ? соответствует их призведение — многочлен из Mn .
Во-вторых. Операции сложения многочленов и умножения многочлена на число — это операции с коэффициентами многочлена, которые являются действительными числами. А для сложения и умножения действительных чисел имеют место равенства 1-8. Нулевым элементом в Mn является многочлен нулевой степени с нулевыми коэффициентами
=(t) = 0·tn + 0·t n-1 + … + 0·t + 0 = 0
И для каждого многочлена
Pn = Pn (t) = antn + an-1t n-1 + … + a1t + a0
Определен противоположный многочлен:
-Pn = -Pn (t) = -antn - an-1t n-1 - … - a1t - a0
2) Определение линейной зависимости системы векторов линейного пространства
Говорят,
что вектор ![]() линейного
пространства L
линейно выражается через
векторы
линейного
пространства L
линейно выражается через
векторы ![]() ,
если его можно представить в виде линейной
комбинации этих
элементов
,
если его можно представить в виде линейной
комбинации этих
элементов ![]() ,
т.е. представить в виде
,
т.е. представить в виде ![]() .
.
Определение. Система ![]() векторов
произвольного линейного пространства
линейно независима если из равенства
векторов
произвольного линейного пространства
линейно независима если из равенства ![]() следует
равенство нулю всех коэффициентов
следует
равенство нулю всех коэффициентов ![]() .
.![]()
Определение. Система векторов, которая не является линейно зависимой, называется линейно независимой.
Пример 1. Векторы a = (1, 1, 1), b = (1, 2, 1) и с = (2, 3, 2) из R3 линейно зависимы, поскольку a + b - с = 0.
Пример 2 Векторы i = (1, 0, 0), j = (0, 1, 0) и k = (0, 0, 1) из R3 линейно независимы, поскольку c1i + c2 j + c3k = 0 означает, что
(c1, c2, c3) = (0, 0, 0),
а это возможно только если
c1 = c2 = c3 = 0.
Необходимое и достаточное условие линейной зависимости системы векторов
Справедливо следующее утверждение.
Теорема. Система векторов произвольного линейного пространства линейно зависима тогда и только тогда, когда хотя бы один вектор системы векторов линейно выражается через остальные векторы системы.
РАЗМЕРНОСТЬ ЛИНЕЙНОГО ПРОСТРАНСТВА
Число k называется размерностью линейного пространства L, если в L существует система из k линейно независимых векторов, а любая система из k+1 вектора — линейно зависима.
Обозначается dimL = k. Пространство L называется k- мерным. Иногда обозначается Lk.
ПРИМЕР
Векторы i и j — линейно независимая система векторов линейного пространства геометрических радиусов-векторов плоскости R2 .
Рассмотрим произвольную систему из трёх векторов x, y, z .
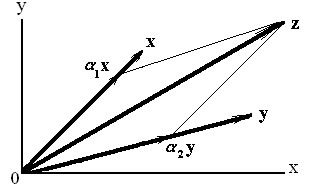
На рисунке показано, что вектор z линейно выражается через векторы x и y: z = α1·x + α2·y.
Итак, в пространстве R2 существует система из двух линейно независимых векторов ( i , j), а любые три вектора образуют линейно зависимую систему. То есть размерность пространства R2 равна 2, dim R2 = 2.
НИЖЕ ЕЩЕ ПРО РАМЕРНОСТЬ, НО ТАМ ВМЕСТЕ С БАЗИСОМ, БАЗИС ПРИСУТСТВУЕТ В ВОПРОСЕ №3
Размерность и базис линейного пространства, координаты вектора
Пусть X — линейное пространство.
Определение. Если существует натуральное число n такое, что X содержит линейно независимую систему из n векторов, а любая система из n + 1 вектора линейно зависима, то X называется n –мерным линейным пространством, а число n – его размерностью.
Будем обозначать n –мерное линейное пространство Xn , где n = dimXn — размерность пространства Xn .
Из определения следует, что размерность линейного пространства равна максимальному количеству линейно независимых векторов.
Замечания.
Размерность пространства, состоящего только из одного нулевого вектора, равна нулю. Такое пространство называется тривиальным.
Если в линейном пространстве существует любое число линейно независимых векторов, то такое пространство называетсябесконечномерным. Мы будем рассматривать, в основном, конечномерные линейные пространства. Бесконечномерные пространства являются предметом специального изучения.
Определение. Упорядоченная система векторов e1, e2, … , en X называется базисом в X , если
система векторов e1, e2, … , en линейно независима;
любой вектор x пространства X может быть представлен в виде
x = ξ1e1 + ξ2e2 + … + ξnen.
(1)
Выражение (1) называется разложением вектора x по базису e1, e2, … , en .
Коэффициенты ξ1, ξ2, … , ξn в разложении векторапо данному базису определяются однозначно.
Доказательство см. в книге О.В. Зиминой ``Линейная алгебра и аналитическая геометрия" (Москва, Изд–во МЭИ, 2000, стр.42).
Коэффициенты разложения (1) вектора x по базису e1, e2, … , en называются координатами вектора x в этом базисе.
Удобно использовать обозначение для i –ой координаты ξi = ei, x и для вектора x = {ξ1, ξ2, … , ξn} . Координаты вектора записывают также в виде матрицы–столбца
ξ1
ξ2
…
ξn
который называется координатным столбцом вектора x .
В n–мерном линейном пространстве Xn существует базис. Он содержит n векторов.
Доказательство см. в книге О.В. Зиминой ``Линейная алгебра и аналитическая геометрия" (Москва, Изд–во МЭИ, 2000, стр.43).
Замечания.
1. В линейном пространстве существует бесчисленное множество базисов.
2. В бесконечномерном пространстве всегда существует базис. Он содержит бесконечное множество векторов. Подробнее о базисах в бесконечномерных пространствах можно прочитать, например, в книге "Функциональный анализ" под ред. С.Г. Крейна (М.: Наука, 1972).
3. Любая упорядоченная линейно независимая система из n векторов в n–мерном пространстве является базисом.
Доказательство см. в книге О.В. Зиминой ``Линейная алгебра и аналитическая геометрия" (Москва, Изд–во МЭИ, 2000, стр.44).
Теорема. Пусть Xn — линейное пространство и e1, e2, … , en — некоторый базис в Xn . Тогда:
При сложении векторов их координаты складываются.
При умножении вектора на число его координаты умножаются на это число.
Доказательство см. в книге О.В. Зиминой ``Линейная алгебра и аналитическая геометрия" (Москва, Изд–во МЭИ, 2000, стр.45).
Утверждения теоремы в наших обозначениях выглядят следующим образом:
ei, x + y = ei, x + ei, y ;
ei, αx = αei, x .
Это означает, что скобки · , · обладают свойством линейности по второму аргументу.
