- •2) Определение линейной зависимости системы векторов линейного пространства
- •Размерность и базис линейного пространства, координаты вектора
- •Подпространство
- •[Править]Свойства подпространств
- •3) Базис линейного пространства
- •6) Линейные преобразования линейного пространства
- •7) Собственные значения и собственные векторы
- •Определение
- •Симметричные матрицы, статистики и моделирования
- •Собственные значения и собственные векторы симметричной матрицы
- •Собственные значения и собственные векторы симметричной матрицы реальные
- •Собственных векторов симметричной матрицы, ортогональны
- •Спектральное разложение симметричной матрицы
- •Проекция матрицы
- •Положительный (полу-) определенных матриц
Подпространство
Алгебраическое
определение: Линейное
подпространство или векторное
подпространство ―
непустое подмножество ![]() линейного
пространства
линейного
пространства ![]() такое,
что
само
является линейным пространством по
отношению к определенным в
действиям
сложения и умножения на скаляр. Множество
всех подпространств обычно обозначают
как
такое,
что
само
является линейным пространством по
отношению к определенным в
действиям
сложения и умножения на скаляр. Множество
всех подпространств обычно обозначают
как ![]() .
Чтобы подмножество было подпространством,
необходимо и достаточно, чтобы
.
Чтобы подмножество было подпространством,
необходимо и достаточно, чтобы
 ;
;для всякого вектора
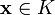 ,
вектор
,
вектор 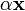 также
принадлежал
,
при любом
также
принадлежал
,
при любом  ;
;для всяких векторов
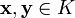 ,
вектор
,
вектор  также
принадлежал
.
также
принадлежал
.
Последние два утверждения эквивалентны следующему:
для
всяких векторов
,
вектор ![]() также
принадлежал
для
любых
также
принадлежал
для
любых ![]() .
.
В
частности, пространство, состоящее из
одного элемента ![]() ,
является подпространством любого
пространства; любое пространство
является само себе подпространством.
Подпространства, не совпадающие с этими
двумя, называют собственными или нетривиальными.
,
является подпространством любого
пространства; любое пространство
является само себе подпространством.
Подпространства, не совпадающие с этими
двумя, называют собственными или нетривиальными.
[Править]Свойства подпространств
Пересечение любого семейства подпространств — снова подпространство;
Сумма конечного семейства подпространств — снова подпространство. Сумма подпространств
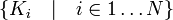 определяется
как множество, содержащее всевозможные
суммы элементов
определяется
как множество, содержащее всевозможные
суммы элементов 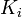 :
:
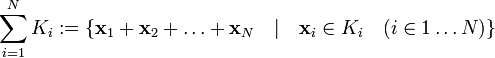 .
.
В функциональном анализе в бесконечномерных пространствах особо выделяют замкнутые подпространства.
3) Базис линейного пространства
Система векторов линейного пространства L образует базис в L если эта система векторов упорядочена, линейно независима и любой вектор из L линейно выражается через векторы системы.
Иными словами, линейно независимая упорядоченная система векторов e1, ..., en образует базис в L если любой вектор x из L может быть представлен в виде
x = С1·e1+С2·e2+ ...+Сn· en.
Можно определить базис иначе.
Любая упорядоченная линейно независимая система e1, ..., en векторов n-мерного линейного пространства Ln образует базис этого пространства.
Поскольку n, размерность пространства Ln— максимальное количество линейно независимых векторов пространства, то система векторов x, e1, ..., en линейно зависима и, следовательно, вектор x линейно выражается через векторы e1, ..., en:
x = x1·e1+ x2·e2+ ...+ xn· en.
Такое разложение вектора по базису единственно.
Разложение вектора по базису.
Определение.
Пусть ![]() –
произвольный вектор,
–
произвольный вектор, ![]() –
произвольная система векторов.
Если выполняется равенство
–
произвольная система векторов.
Если выполняется равенство
![]() ,
(1)
,
(1)
то
говорят, что вектор
представлен
в виде линейной комбинации
данной системы векторов.
Если данная система векторов
является
базисом векторного пространства,
то равенство (1)
называется разложением вектора
по
базису
. Коэффициенты
линейной комбинации ![]() называются
в этом случае координатами
вектора
относительно
базиса
.
называются
в этом случае координатами
вектора
относительно
базиса
.
Теорема. (О разложении вектора по базису.)
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
Доказательство. 1) Пусть L произвольная
прямая (или ось) и ![]() –базис
–базис ![]() .
Возьмем произвольный вектор
.
Возьмем произвольный вектор ![]() .
Так как оба вектора
.
Так как оба вектора ![]() и
коллинеарные
одной и той же прямой L,
то
и
коллинеарные
одной и той же прямой L,
то ![]() .
Воспользуемся теоремой о
коллинеарности двух векторов.
Так как
.
Воспользуемся теоремой о
коллинеарности двух векторов.
Так как ![]() ,
то найдется (существует) такое число
,
то найдется (существует) такое число ![]() ,
что
,
что ![]() и
тем самым мы получили разложение
вектора
по
базису
векторного пространства
.
и
тем самым мы получили разложение
вектора
по
базису
векторного пространства
.
Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису векторного пространства :
и ![]() ,
где
,
где ![]() .
Тогда
.
Тогда ![]() и
используя закон дистрибутивности,
получаем:
и
используя закон дистрибутивности,
получаем:
![]() .
.
Так как
,
то из последнего равенства следует,
что ![]() ,
ч.т.д.
,
ч.т.д.
2) Пусть теперь
Р произвольная плоскость и ![]() – базис
– базис ![]() .
Пусть
.
Пусть ![]() произвольный
вектор этой плоскости. Отложим все три
вектора от какой-нибудь одной точки
этой плоскости. Построим 4 прямых.
Проведемпрямую
произвольный
вектор этой плоскости. Отложим все три
вектора от какой-нибудь одной точки
этой плоскости. Построим 4 прямых.
Проведемпрямую ![]() ,
на которой лежит вектор
, прямую
,
на которой лежит вектор
, прямую ![]() ,
на которой лежит вектор
,
на которой лежит вектор ![]() .
Через конец вектора
проведем прямую параллельную
вектору
и
прямую параллельную вектору
.
Эти 4 прямые высекают
параллелограмм. См. ниже рис. 3. По правилу
параллелограмма
.
Через конец вектора
проведем прямую параллельную
вектору
и
прямую параллельную вектору
.
Эти 4 прямые высекают
параллелограмм. См. ниже рис. 3. По правилу
параллелограмма ![]() ,
и
,
и ![]() ,
, ![]() ,
– базис
,
,
– базис
, ![]() – базис
.
– базис
.
Теперь,
по уже доказанному в первой части этого
доказательства, существуют такие числа ![]() ,
что
,
что
![]() и
и ![]() .
Отсюда получаем:
.
Отсюда получаем:
![]() и
возможность разложения по базису
доказана.
и
возможность разложения по базису
доказана.

рис.3.
Теперь
докажем единственность разложения по
базису. Допустим противное. Пусть имеется
два разложения вектора
по
базису
векторного пространства
: ![]() и
и ![]() .
Получаем равенство
.
Получаем равенство
![]() ,
откуда следует
,
откуда следует ![]() .
Если
.
Если ![]() ,
то
,
то ![]() ,
а т.к.
,
а т.к. ![]() ,
то
,
то ![]() и
коэффициенты разложения равны:
и
коэффициенты разложения равны: ![]() ,
, ![]() .
Пусть теперь
.
Пусть теперь ![]() .
Тогда
.
Тогда ![]() ,
где
,
где ![]() .
По теореме о коллинеарностидвух векторов отсюда
следует, что
.
По теореме о коллинеарностидвух векторов отсюда
следует, что ![]() .
Получили противоречие условию теоремы.
Следовательно,
и
,
ч.т.д.
.
Получили противоречие условию теоремы.
Следовательно,
и
,
ч.т.д.
3)
Пусть ![]() – базис
– базис ![]() и
пусть
и
пусть ![]() произвольный
вектор. Проведем следующие построения.
произвольный
вектор. Проведем следующие построения.
Отложим все
три базисных вектора ![]() и
вектор
от
одной точки и построим 6 плоскостей:
плоскость, в которой лежат
базисные векторы
и
вектор
от
одной точки и построим 6 плоскостей:
плоскость, в которой лежат
базисные векторы ![]() , плоскость
, плоскость ![]() и плоскость
и плоскость ![]() ;
далее через конец вектора
проведем
три плоскости параллельно
только что построенным трем плоскостям.
Эти 6 плоскостей высекают
параллелепипед:
;
далее через конец вектора
проведем
три плоскости параллельно
только что построенным трем плоскостям.
Эти 6 плоскостей высекают
параллелепипед:
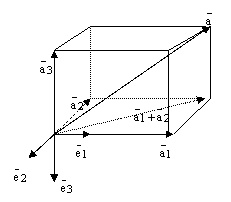
рис.4.
По правилу сложения векторов получаем равенство:
![]() .
(1)
.
(1)
По построению ![]() .
Отсюда, по теореме о коллинеарности двухвекторов,
следует, что существует число
.
Отсюда, по теореме о коллинеарности двухвекторов,
следует, что существует число ![]() ,
такое что
,
такое что ![]() .
Аналогично,
и
.
Аналогично,
и ![]() ,
где
,
где ![]() .
Теперь, подставляя эти равенства в (1),
получаем:
.
Теперь, подставляя эти равенства в (1),
получаем:
![]() (2)
(2)
и возможность разложения по базису доказана.
Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису :
и ![]() .
Тогда
.
Тогда
![]() .
(3)
.
(3)
Заметим, что по условию векторы некомпланарные, следовательно, они попарно неколлинеарные.
Возможны два случая: или .
а) Пусть , тогда из равенства (3) следует:
![]() .
(4)
.
(4)
Из равенства
(4) следует, что вектор
раскладывается
по базису ![]() ,
т.е. вектор
лежит
в плоскости векторов
и,
следовательно, векторы
компланарные,
что противоречит условию.
,
т.е. вектор
лежит
в плоскости векторов
и,
следовательно, векторы
компланарные,
что противоречит условию.
б) Остается
случай
,
т.е. ![]() .
Тогда из равенства (3) получаем
.
Тогда из равенства (3) получаем ![]() или
или
![]() .
(5)
.
(5)
Так
как
– базис пространства векторов лежащих
в плоскости, а мы уже доказали единственность
разложения по базису векторов плоскости,
то из равенства (5) следует, что
и ![]() ,
ч.т.д.
,
ч.т.д.
Теорема доказана.
Координаты вектора.На плоскости координаты вектора v относительно данного базиса (a, b) – это такая пара чисел (x; y), что v = xa + yb. Любой вектор имеет однозначно определенные координаты относительно любого базиса.
При сложении векторов складываются их соответственные координаты; при умножении вектора на число каждая координата умножается на это число. Скалярное произведение векторов с координатами (x; y) и (x'; y') равно сумме произведений соответственных координат: xx' + yy'.
Чтобы вычислить
координаты вектора ![]() ,
зная координаты (x1; y1)
его начала A и
координаты (x2; y2)
его конца B, нужно
из координат конца вычесть координаты
начала: (x2 – x1; y2 – y1).
,
зная координаты (x1; y1)
его начала A и
координаты (x2; y2)
его конца B, нужно
из координат конца вычесть координаты
начала: (x2 – x1; y2 – y1).
Все сказанное справедливо и для случая пространства с той разницей, что базис в пространстве состоит из трех векторов, а наборы координат векторов и точек – из трех чисел.
Прямые x, y, z называются координатными осями (или осями координат), точка их пересечения O – началом координат, а плоскости xOy, xOz и yOz – координатными плоскостями. Точка O разбивает каждую координатную ось на две полупрямые, которые называютсяположительной и отрицательной полуосями.
Координатой точки A по оси x будем называть число, равное по абсолютной величине длине отрезка OAx: положительное, если точка A лежит на положительной полуоси x, и отрицательное, если она лежит на отрицательной полуоси.
Аналогично можно определить координаты y и z точки A. Координаты точки A записываются в скобках рядом с названием этой точки: A (x; y; z).
|
|
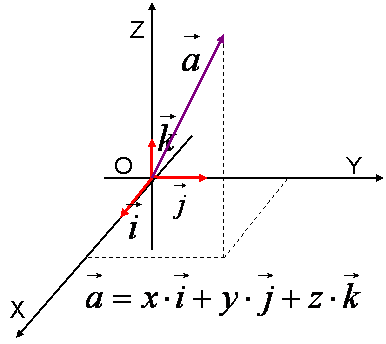
Единичным вектором или ортомназывается вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси. Единичный
вектор, направленный вдоль оси x,
обозначается i Единичный вектор, направленный вдоль осиy, обозначается j . Единичный вектор, направленный вдоль оси z, обозначается k . Вектора i , j , k называются координатными векторами. Любой
вектор a
можно
разложить по координатным
векторам: a
=x Коэффициенты разложения определяются единственным образом и называются координатами вектора a в данной системе координат. |
|
Свойства векторов, заданных координатами
Координаты нулевого вектора равны нулю.
Координаты равных векторов соответственно равны.
Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов.
Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов.
Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число.
Формулы
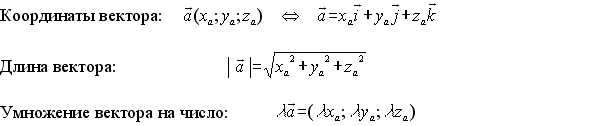
Угол
между
векторами: a![]() (xa;ya;za)
(xa;ya;za)![]() b
(xb;yb;zb)
b
(xb;yb;zb)![]() cos
cos![]() =xa
=xa![]() xb+ya
yb+za
zb
xb+ya
yb+za
zb![]() x2a+ya2+za2
x2a+ya2+za2
![]() x2b+yb2+zb2
x2b+yb2+zb2
Перпендикулярность
векторов: a
(xa;ya;za)
b
(xb;yb;zb)
a
![]() b
=0
b
=0![]() xa
xb+ya
yb+za
zb=0
xa
xb+ya
yb+za
zb=0
Коллинеарность векторов: a (xa;ya;za) b (xb;yb;zb) xbxa=ybya=zbza если координаты векторов не равны нулю.