6) Линейные преобразования линейного пространства

     Определение линейного оператора

     Преобразование (оператор, отображение) f линейного пространства в себя (запись ) называется линейным, если:

     

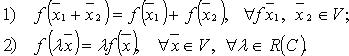
     Условия 1 и 2 равносильны соотношению

     Матрица линейного оператора

     Матрица линейного оператора в базисе ( ) - матрица

столбцами которой являются столбцы образов базисных векторов оператора f, т. е.

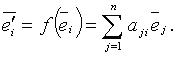
     Линейный оператор называется невырожденным, если

     Связь между координатами вектора и его образа

     Если в базисе ( ) имеет координатный столбец - линейный оператор с матрицей A в данном базисе, - координатный столбец вектора , то Y = AX (употребляется также запись ). Более подробно:

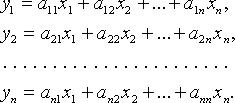
     Связь между матрицами одного и того же линейного оператора в разных базисах

     Если в базисе линейный оператор имеет матрицу A, в базисе - матрицу B, а S - матрица перехода от первого базиса ко второму, то

     Произведение и сумма линейных операторов

     Если f и g - линейные операторы пространства с матрицами A и B в базисе , то операторы произведения и суммы - линейные и имеют в том же базисе матрицы BA и A + B соответственно.

     Оператор, обратный данному линейному оператору

     Линейный оператор называется обратным линейному оператору , если

     Обозначение:

     Для существования необходимо и достаточно, чтобы f был невырожденным оператором. Если A - матрица оператора f в некотором базисе, то оператор в том же базисе имеет матрицу .

     Ядро и область значений линейного оператора

     Ядро оператора: - множество, обозначаемое Ker f:

     Область значений (образ) оператора - множество, обозначаемое Im f:

     Множества Ker f и Im f являются подпространствами пространства V.

     Ранг оператора (обозначение: dim Im f) - ранг матрицы A линейного оператора f,

dim Im f = rank A.

     Дефектом оператора называют dim Ker f,

dim Im f + dim Ker f = n.

Собственные векторы и собственные значения линейного оператора

     Ненулевой вектор называется собственным вектором линейного оператора , если ( для комплексного ), такое, что Число называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору.

     Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор имеет координатный столбец X, то или

     Собственные числа линейного оператора - корни характеристического уравнения , где - матрица оператора f, - символ Кронекера.

     Для каждого собственного значения соответствующие собственные векторы могут быть найдены из матричного уравнения или соответствующей ему системы линейных уравнений

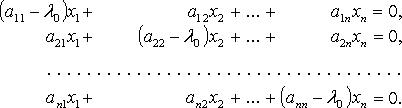
     Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид

где - соответствующие собственные значения.

7) Собственные значения и собственные векторы

Определение. Пусть . Характеристический многочлен А

(I, единичная матрица).

Корень характеристического многочлена называется собственным (или характерное значение) А.

В то время как элементы приходят с поля F, то имеет смысл обратиться за корни в E расширение поля F. Например, если матрица с вещественными элементами, вы можете попросить для собственных в или в .

Пример. Рассмотрим матрицу

Характеристический многочлен . Таким образом, не имеет собственных значений в . Его собственные значения в являются .

Пример. Пусть

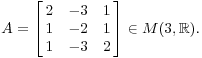
Вы можете использовать строки и столбца операций для упрощения расчета :

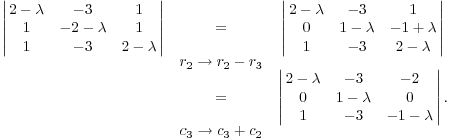
(Добавление нескольких из строки или столбца в строке или столбце, соответственно, не меняет определителя.) Теперь увеличится на сомножители второго ряда:

Собственные значения , (Двухместный).

Пример. Матрицы является верхней треугольной, если для . Таким образом, элементы ниже главной диагонали, равны нулю. (Нижних треугольных матриц определяется аналогичным образом.)

Собственные матрица

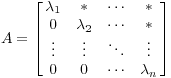
только диагональные элементы . (Вы можете доказать это индукцией по п).

Замечание. Чтобы найти собственные значения матрицы, вам нужно найти корни характеристического многочлена.

Есть формулы для нахождения корней многочленов степени . (Например, квадратичная формула дает корни квадратного уравнения ). Однако, Абель показал в первой половине 19-го века, что квинтика вообще не разрешимы в радикалах. (Например, не разрешимо в радикалах над .) В реальном мире, вычисления собственных часто требует численного приближения.

Если есть собственное значение, то . Таким образом, матрица не является обратимым. Отсюда следует, что должны уменьшить строки к строке уменьшить эшелона матрицы R с меньшим, чем п старшими коэффициентами. Таким образом, система имеет по крайней мере одной свободной переменной, и, следовательно, имеет более одного решения. В частности, --- И, следовательно, --- По крайней мере одно ненулевое решение.

Определение. Пусть , И пусть является собственным А. собственным (или характеристика вектор) для ненулевой вектор такой, что

Это равносильно тому,

Пример. Пусть

Собственные значения , (Двухместный).

Во-первых, я найду для собственного .

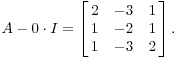
Я хочу такой, что

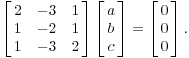
Вы можете решить систему, ряд сокращения. Поскольку колонки нулей справа никогда не изменится, этого достаточно, чтобы грести уменьшить Матрица справа.

Это говорит о

Таким образом, , , А собственный вектор

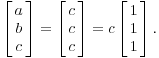
Обратите внимание, что это обычный алгоритм нахождения основой для пространства решений однородной системы (или нуль-пространство матрицы).

Я могу установить с любым ненулевым числом. Например, дает собственный вектор . Обратите внимание, что существует бесконечное множество собственных векторов для этого собственные значения, но все эти собственные кратные .

Кроме того,

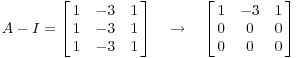
Таким образом, собственные векторы

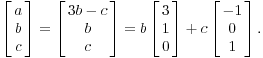
Принимая , дает , С , дает . Это собственное приводит к возникновению двух независимых собственных векторов.

Однако следует отметить, что двойной корень характеристического многочлена не обязательно дают два независимых собственных векторов.

Определение. Матрицы подобными, если существует обратимая матрица такой, что .

Лемма. Подобные матрицы имеют одинаковые характеристики многочлена (и, следовательно, те же собственные значения).

Доказательство.

Таким образом, матрицы и схожи. Следовательно, они имеют тот же определитель. Определитель является характеристическим многочленом и определителем является характеристическим многочленом .

Определение. Пусть быть линейным преобразованием, где V-конечномерное векторное пространство. Характеристический многочлен T является характеристический многочлен матрицы T по отношению к основе В.

Предыдущая лемма показывает, что это зависит от выбора базиса. Ибо, если и являются основой для V, то

Таким образом, и схожи, поэтому они имеют такие же характеристический многочлен.

Это показывает, что имеет смысл говорить о собственных значениях и собственных векторов линейного преобразования Т.

Определение. Матрица диагонализируема если имеет n независимых собственных --- то есть, если есть основания для , состоящий из собственных векторов А.

Предложение. диагонализируема тогда и только тогда он похож на диагональную матрицу.

Доказательство. Пусть быть п независимых собственных векторов, отвечающих собственным значениям . Пусть T линейное преобразование соответствующего:

С для всех г, матрица Т в базисе есть

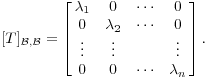
Теперь есть матрица T по отношению к стандартной основе, так

Матрица получается путем создания матрицы с использованием как колонны. Затем .

Таким образом,

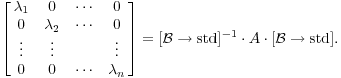
И наоборот, если D диагональная, Р обратим, и , Столбцы Р независимых собственных векторов для А. В самом деле, если

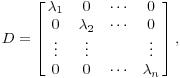
затем говорит

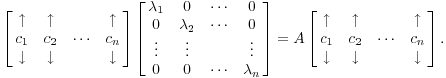
Таким образом, .

Пример. Рассмотрим матрицу матрицей

В предыдущем примере я показал, что имеет 3 независимых собственных , , . Таким образом, диагонализируема.

Чтобы найти диагонализации матрицы, построить матрицу с помощью собственных, как столбцы:

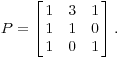
Вы можете проверить, находя и делать умножения, что вы получите диагональ матрицы:

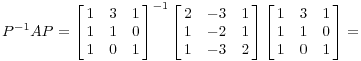
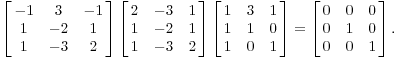
Конечно, я знал, что это был ответ! Я должен получить диагональную матрицу с собственными значениями на главной диагонали, в том же порядке, что я поставил соответствующие собственные векторы в П.

Вы можете поставить собственных в качестве столбцов P в любом порядке: различный порядок даст диагональная матрица с собственными значениями на главной диагонали в другом порядке.

Пример. Пусть

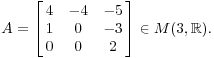
Найти собственные значения и для каждого собственного значения, полный набор собственных векторов. Если диагонализируема, найти матрицы Р такой, что является диагональной матрицей.

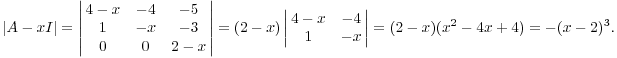
Собственное значение .

Сейчас

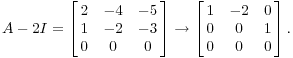
Думать об этом как коэффициент матрицы однородной линейной системы с переменными, б, в, я получим уравнения

Затем , Так что

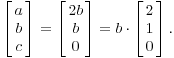
является собственным вектором. Так как есть только одна независимая собственным --- в отличие от 3 --- матрица не диагонализируема.

Пример. Следующий matrixhas собственное (Тройной корень):

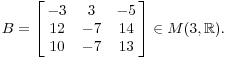
Сейчас

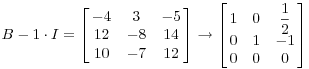
Думать об этом как коэффициент матрицы однородной линейной системы с переменными, б, в, я получим уравнения

Установка . Это дает и . Таким образом, только собственные векторы ненулевых кратных . Так как есть только одна независимая собственных, B не диагонализируема.

Предложение. Пусть быть линейное преобразование на п-мерное векторное пространство. Если являются собственные векторы, соответствующие различным собственным значениям , То является независимой.

Доказательство. Предположим противное, что зависит. Пусть р-наименьшее число такое, что множество зависит. Тогда существует нетривиальная линейная зависимость

Обратите внимание, что , В противном случае

Это противоречило бы минимальности р.

Таким образом, я могу переписать уравнение выше в виде

Применение T для обеих сторон, а также использовать :

С другой стороны,

Вычтем последнее равенство от одного до его получения

Так как собственные значения различны, то условия отличны от нуля. Следовательно, это линейная зависимость в что противоречит минимальности р --- если .

В этом случае, , Что противоречит тому, что является собственным вектором. Таким образом, первоначальный набор должен быть фактически независимыми.

Пример. Пусть вещественная матрица. Комплекс собственных всегда приходят в сопряженных парах и .

Более того, если V является собственным для , То сопряженный является собственным для .

Действительно, предположим, . Принимая комплексно сопряженные, я получаю

( потому что реальная матрица).

В практическом плане это означает, что как только вы нашли собственный для одного комплекса собственное значение, вы можете получить собственный вектор для сопряженных собственных значений, принимая сопряженное собственный вектор. Вам не нужно делать отдельный собственный расчет.

Например, предположим,

Характеристический многочлен . Собственные значения .

Найти собственного вектора :

Я знал, что во втором ряду должно быть кратно первой строки, потому что я знаю, что система имеет нетривиальные решения. Так что я не должен работать, что это несколько, я могу только обнулить второй ряд общих принципов.

Это работает только для матриц, а только для тех, которые Автора в собственный вычислений.

Далее, нет никакого смысла в пройдя весь путь к строке приведенную форму эшелона. Мне просто нужно некоторый ненулевой вектор такой, что

То есть, я хочу

Я могу найти а и б, которые работают путем замены и 1, и отрицание одного из них. Например, возьмем (-1 Отрицается) и . Это проверка:

Так является собственным для .

К обсуждению в начале, например, мне не нужно, чтобы сделать вычисления для . Просто сопряженные предыдущим собственным: должно быть собственным для .

Так как 2 независимых векторов, то вы можете использовать их, построить диагонализации матрицы:

Обратите внимание, что вы получите диагональная матрица с собственными значениями на главной диагонали, в том же порядке, в котором Вы перечислили собственные.

Пример. Для следующей матрицы, найти собственные значения за , И для каждого собственного значения, полный набор независимых собственных векторов.

Найти диагонализации матрицы и соответствующие диагональные матрицы.

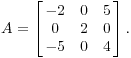
Характеристический многочлен

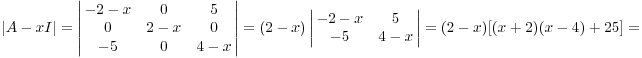
Сейчас

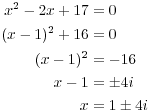
Собственные значения и .

Для , У меня есть

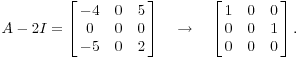
С переменным, б, в, соответствующей однородной системы и . Это дает вектор решения

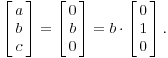
Принимая Я получить собственный вектор .

Для , У меня есть

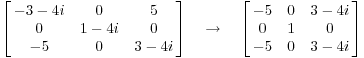
Я умножил первый ряд, , А затем разделил его на 5. Это сделало его таким же, как в третьем ряду.

Я разделил вторую строку, .

(Я знал, что первая и третья строки должны быть кратными, так как они четко зависит от второй строки. Таким образом, если они не кратны, три ряда были бы независимыми, собственный вектор матрицы будет обратимым, и не будет собственных [которые должны быть отличны от нуля].)

Теперь я могу уничтожить третьего ряда путем вычитания первой:

С переменным, б, в, соответствующей однородной системы

Там будет только один параметр (с), так что будет только один независимый собственный вектор. Чтобы получить один, переключение "-5" и " »И свести на нет" -5 ", чтобы получить" 5 ". Это дает , И . Вы можете видеть, что эти значения и работы с:

Таким образом, мой собственный вектор .

Таким образом, собственный для сопряженная .

Диагонализации матрицы задается

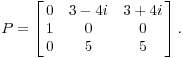
С этой диагонализации матрицы, у меня есть

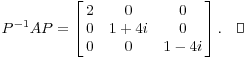
8) Симметричная матрица