6.10 Перша теорема розвинення

Теорема: Якщо зображення являє собою степеневий ряд за відємними степенями р з ненульовим радіусом збіжності, тобто, якщо

(6.10.1)

то оригіналом зображення є степеневий ряд за невідємними степенями , тобто

(6.10.2)

який збігається при усіх .

Очевидно, що формальна відповідність рядів (5.10.1) і (5.10.2) мається, бо .

Доводиться, що ряд (6.10.2) сходиться рівномірно і його сума дорівнює оригіналу для функції .

Приклад 1. Знайти оригінал функції

Розвязання

Функція є сумою степеневого ряду, що збігається при , тобто

Отже, на підставі першої теореми розвинення, маємо:

.

Відповідь:

.

6.11 Друга теорема розвинення

Теорема: Якщо зображення – правильний раціональний нескоротний дріб, знаменник , якого має лише прості корені , тобто , то

, (6.11.1)

де

.

Доведення

Як відомо, у випадку простих коренів знаменника правильний раціональний дріб розкладається на найпростіші дроби в такий спосіб:

Множення обох частин цієї рівності на двочлен дає:

відкіля, переходячи до границі при , визначається

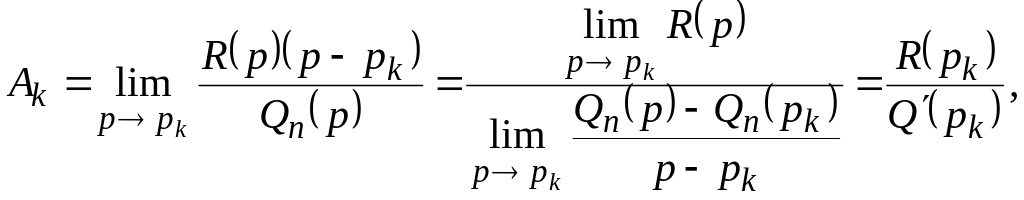
причому , бо – простий корінь. Далі за теоремою зсуву , а на підставі властивості лінійності зображення

.

Приклад 1. Знайти оригінал функції .

Розвязання

За другою теоремою розвинення, маємо:

.

Відповідь:

.

Цей же приклад можна розвязати і наступним шляхом:

.

7 Таблиця основних відповідностей

«оригінал» – «зображення»

№ п/п	Оригінал	Зображення
1
2	1
3
4
5
6
7
8
9
10
11
12
13
14
15
16
№ п/п	Оригінал	Зображення
17
18
19

8 Розвязання звичайних лінійних диференціальних рівнянь з постійними коефіцієнтами операційним методом

Нехай необхідно розвязати задачу Коші

(8.1)

для диференціального рівняння -го порядку

(8.2)

де – дійсні числа – задані числа (початкові умови).

Задачу (8.1), (8.2) можна розвязати, отримавши спочатку загальне розвязання рівняння (8.2), яке є сумою загального розвязку відповідного однорідного (без правої частини) рівняння і будь-якого окремого розвязку рівняння (8.2). Загальний розвязок рівняння (8.2) має довільних сталих, які визначаються таким чином, щоб задовольнялися початкові умови (8.1).

Але, значно простіше і раціональніше задача Коші (8.1), (8.2) розвязується операторним методом.

При розвязанні задачі (8.1), (8.2) операційним методом передбачається, що шукана функція , усі її розглянуті похідні, а також функція (права частина рівняння (8.2)) є функціями-оригіналами.

Нехай і .

За формулою диференціювання оригіналу

і початковими умовами (8.1) маємо:

…………………………………………...... (8.3)

Далі, користаючись властивістю лінійності і ураховуючи відповідності (8.3), переходять від диференціального рівняння (8.2) до відповідного йому алгебраїчному рівнянню щодо зображення шуканої функції , які є розвязком задачі (8.1), (8.2):

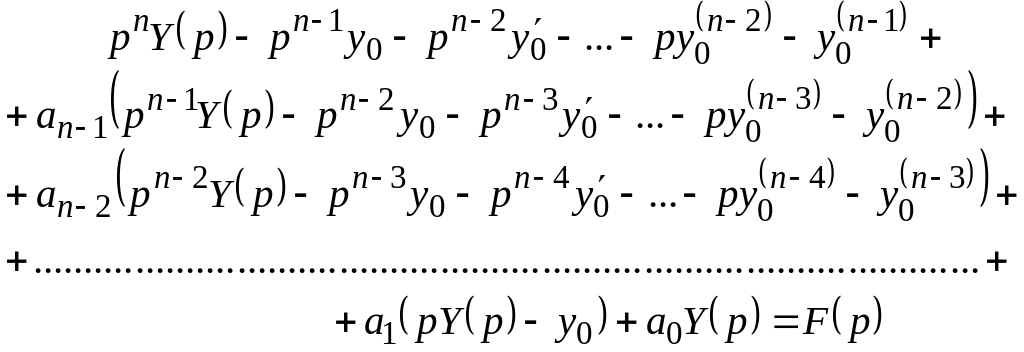
або

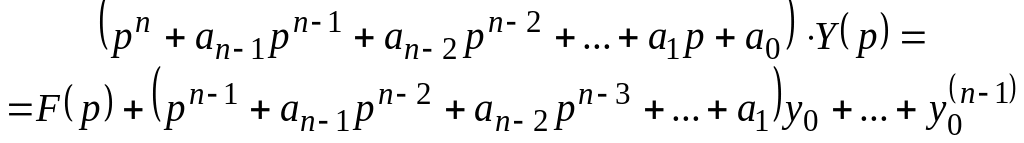
або коротко

(8.4)

де і – алгебраїчні багаточлени степенів і відповідно щодо параметра р.

Рівняння (8.4) називається рівнянням у зображеннях, що відповідає диференціальному рівнянню (8.2).

Розвязок рівняння (8.4)

(8.5)

називається операторним розвязком диференціального рівняння (8.2).

Оригінал y(t), для якого функція Y(p) (8.3) є зображенням, і буде шуканим (причому єдиним у силу теореми єдиності) розвязком задачі (8.1), (8.2):

(8.6)

Приклад 1. Розвязати задачу Коші

(8.1)

для рівняння

. (8.2)

Розвязання

Нехай шукана функція і її похідні є оригіналами і нехай . Тоді

(8.3)

.

Підставивши замість і правої частини в задане диференціальне рівняння відповідні їм зображення, переходять до рівняння в зображеннях:

(8.4)

відкіля

Відповідь:

Перевірка.

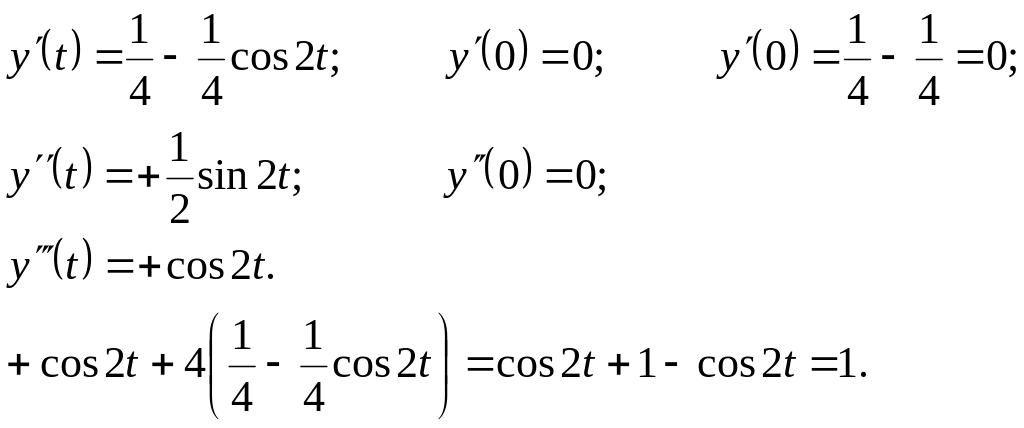
Приклад 2. Розвязати задачу Коші

(8.1)

. (8.2)

Розвязання

Нехай . Тоді , а

Отже, рівняння в зображеннях приймає вид:

або

відкіля

Відповідь:

Перевірка

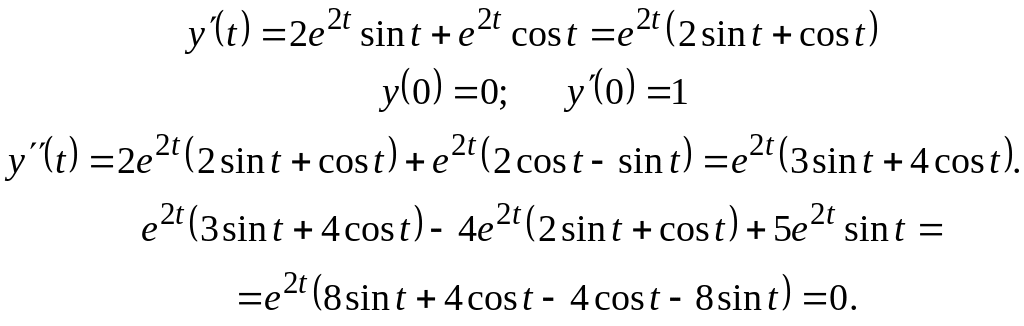
Примітка

Перевага операційного методу інтегрування диференціального рівняння перед класичним методом полягає в тому, що при розвязанні операційним методом отримуємо розвязання диференціального рівняння, що задовольняє заданим початковим умовам, по ходу його розвязання, минаючи одержання загального інтегралу заданого диференціального рівняння. Якщо ж потрібно знайти загальний інтеграл (загальний розвязок) диференціального рівняння (8.2), то і його можна одержати операційним методом.

Приклад 3. Знайти загальний розвязок диференціального рівняння операційним методом.

Розвязання

Для одержання загального розвязку (інтегралу) беруться довільні початкові умови , . Тоді рівняння в зображеннях буде:

відкіля

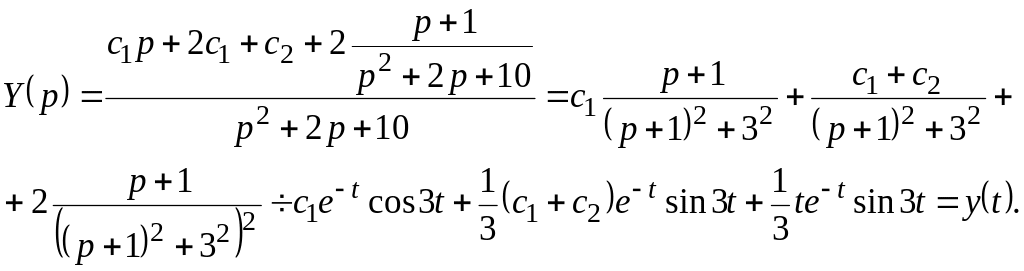
Відповідь:

де – довільна стала.