Вступ

Операційне числення широко застосовується на практиці при розв’язанні різних задач науки і техніки. Особливо широке застосування воно має при дослідження перехідних процесів у лінійних фізичних системах електротехніки, автоматики, радіотехніки і телемеханіки.

Сучасний математичний апарат операційного числення дозволяє розв'язувати задачі математичними моделями яких є системи лінійних диференціальних рівнянь (звичайних і з частними похідними), різницеві і диференційно-різницеві рівняння та деякі типи інтегральних рівнянь. Велика універсальність операційного числення при розв’язанні задач пояснюється можливістю отримати їх розв’язки найбільш раціональним шляхом.

В методичному посібнику наведені відповіді на теоретичні питання по курсу “Операційне числення”.

1 Деякі питання теорії комплексної змінної

1.1 Комплексне число та дії над ним

Комплексним числом z називається пара дійсних чисел (a, b) із установленим порядком проходження чисел a й b. Це умовно записується у вигляді z = (а, b). Перше число а пари (а, b) називається дійсною частиною комплексного числа z і позначається символом а = Re z, друге число b пари (а, b) називається мнимою частиною комплексного числа z і позначається символом b = Im z.

Два комплексних числа рівні тоді й тільки тоді, коли рівні їх дійсні й мнимі частини, тобто коли

Перейдемо до визначення алгебраїчних операцій над комплексними числами.

Сумою комплексних чисел називається таке комплексне число z = (a, b), для якого Легко бачити, що при такому визначенні зберігаються переміщувальний і сполучний закони додавання, тобто й Так само, як й в області дійсних чисел, нулем називається таке комплексне число 0, сума якого з кожним комплексним числом z дорівнює цьому числу z, тобто z + 0 = z. Очевидно, що існує єдине комплексне число 0 = (0,,0), що володіє цією властивістю.

Добутком комплексних чисел називається таке комплексне число z = (a, b), для якого При такому визначенні добутку виконуються переміщувальний , сполучний і розподільний закони.

Включимо дійсні числа в множину комплексних чисел, розглядаючи дійсне число а як комплексне число а = (а,0). Тоді, як треба з визначення дій додавання й множення, для комплексних чисел зберігаються відомі правила дій над дійсними числами.

Тому множина комплексних чисел розглядається як розширення множини дійсних чисел. Помітимо, що множення на дійсну одиницю (1,0) не міняє комплексного числа: z * 1 = z.

Комплексне число виду z = (0, b) називається чисто - мнимим і символічно позначається як z = ib. Чисто уявне число (0, b) = ib можна розглядати як добуток мнимої одиниці (0,1) і дійсного числа (b,0). Мниму одиницю звичайно позначають символом (0,1) =i. У силу визначення добутку комплексних чисел справедливе співвідношення Воно дозволяє додати прямий алгебраїчний зміст, так називаній алгебраїчній формі запису комплексного числа

(1.1)

і робити операції додавання й множення комплексних чисел за звичайними правилами алгебри багаточленів.

Комплексне число z = а - ib називається комплексно сполученим числу z = а + ib.

Операція вирахування комплексних чисел визначається як операція, зворотна додаванню. Комплексне число z = a + ib називається різницею комплексних чисел , якщо

Операція ділення комплексних чисел визначається як операція, зворотна множенню. Комплексне число z = а + ib називається часткою комплексних чисел , якщо з знаменником відмінним від нуля.

(1.2)

1.2 Геометрична інтерпретація комплексних чисел

Оскільки комплексне число визначається як пара дійсних чисел, те природною геометричною інтерпретацією є зображення комплексного числа z = а + ib точкою площини ху з декартовими координатами х = а й у = b. Число z = 0 ставиться у відповідність початку координат даної площини. Таку - площина ми надалі будемо називати комплексною площиною, вісь абсцис — дійсної, а вісь ординат — мнимою віссю комплексної площини. При цьому, мабуть, установлюється взаємно однозначна відповідність між множиною всіх комплексних чисел і множиною крапок комплексної площини, а також між множиною всіх комплексних чисел z = a+ib і множиною вільних векторів, проекції х и у яким на осі абсцис й ординат відповідно рівні а й b.

Дуже важливою є також інша форма подання комплексних чисел. Для визначення положення крапки на площині можна користуватися полярними координатами де - відстань крапки від початку координат, а - кут, що становить радіус-вектор даної крапки з позитивним напрямком осі абсцис. Позитивним напрямком зміни кута вважається напрямок проти вартовий стрілки .Скориставшись зв'язком декартових і полярних координат: , одержимо так називану тригонометричну форму запису комплексного числа:

(1.3)

При цьому звичайно називають модулем, а — аргументом комплексного числа й позначають . Попередні формули дають вираження дійсної й мнимої частин комплексного числа через його модуль й аргумент. Легко виразити модуль й аргумент комплексного числа через його дійсну й мниму частини: (при виборі з рішень останнього рівняння значення варто врахувати знаки а й b). Відзначимо, що аргумент комплексного числа визначений не однозначно, а з точністю до адитивного що складає, кратного .

Два відмінних від нуля комплексні числа рівні між собою в тім і тільки в тому випадку, якщо рівні їхні модулі, а значення аргументів або рівні, або відрізняються на число, кратне .

Комплексно сполучені числа мають той самий модуль, а значення їхніх аргументів, при відповідному виборі областей їхньої зміни, розрізняються знаком.

Нарешті, використовуючи відому формулу Ейлера , одержуємо показову форму запису комплексного числа: (1.4)

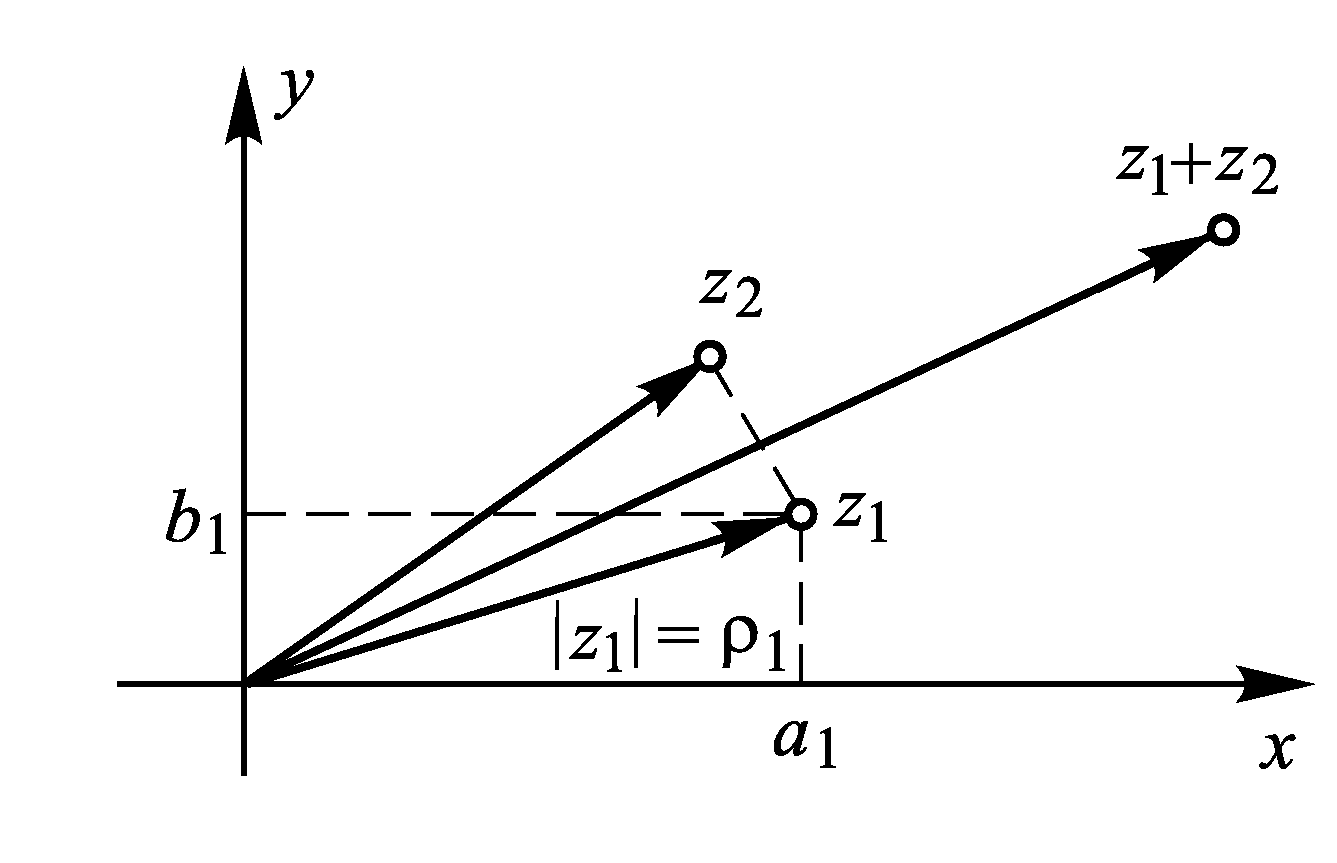
Рисунок 1- Операції над векторами

Відзначене вище відповідність між множиною всіх комплексних чисел і плоских векторів дозволяє ототожнити операції додавання й вирахування комплексних чисел з відповідними операціями над векторами (рисунок 1). При цьому легко встановлюються нерівності трикутника:

(1.5)

Модуль різниці двох комплексних чисел має геометричний сенс відстані між відповідними крапками на комплексній площині. Відзначимо, крім того, очевидні нерівності .

Для виконання операції множення зручно користуватися тригонометричною формою подання комплексних чисел. Відповідно до правил множення одержуємо

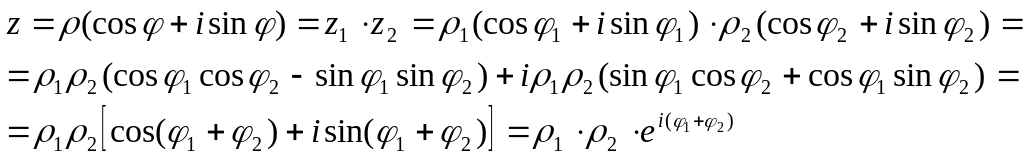(1.6)

звідси, , тобто модуль добутку дорівнює добутку модулів, а аргумент — сумі аргументів співмножників. У випадку ділення комплексних чисел при має місце аналогічне співвідношення:

(1.7)