6.1 Теорема подібності

Вплив на зображення зміни масштабу осі , на якій визначений оригінал , розкривається наступною теоремою:

Теорема: Якщо (додатне число) і , то , тобто множення аргументу оригіналу на додатне число приводить до ділення зображення і його аргументу на це число.

Доведення

Нехай , де , – оригінал. Тоді . Заміна змінної в інтегралі , отже, , при , а при , дає

(6.1.1)

Приклад 1. З формули на підставі теореми подібності маємо:

Приклад 2. З формули на підставі теореми подібності маємо:

Або другим шляхом:

6.2 Властивість лінійності зображення

Теорема: Зображення суми декількох оригіналів, помножених на сталі величини дорівнює сумі зображень цих оригіналів, помножених на відповідні сталі, тобто, якщо

(6.2.1)

де – сталі і , то

(6.2.2)

Доведення

Множення всіх членів рівності (5.1) на та інтегрування отриманої рівності в межах від 0 до дає:

Приклад 1. Знайти зображення за Лапласом функції

Розвязання

На підставі формул і властивості лінійності зображення маємо:

Приклад 2. Знайти оригінал (початкову функцію), зображення якої виражається формулою

Розвязання

На підставі властивості лінійності зображення виходить

З теореми єдності зображення випливає, що це єдина початкова функція (оригінал), що відповідає даній функції

6.3 Теорема загоювання

Теорема. Якщо – додатне число й оригіналу , то

Доведення

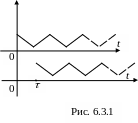
Поклавши визначається

,

тобто

.

Таким чином, загоювання (запізнення) аргументу оригіналу на додатну величину приводить до множення зображення оригіналу без загоювання на .

Приклад. У пункті 4 було встановлено, що для одиничної функції Хевісайда: , значить для функції маємо

6.4 Теорема зсуву

Теорема: Якщо є зображення функції , то – зображення функції тобто, якщо , то (Тут передбачається, що ).

Доведення

(6.4.1)

Приклад 1. Знайти зображення функцій і .

Розвязання

З формули на підставі теореми зсуву випливає:

Аналогічно, з формули на підставі теореми зсуву:

Теорема зсуву може розглядатися і як одна зі зворотних теорем, що дозволяють знаходити оригінали за заданими їх зображеннями. А саме, якщо відомо оригінал для зображення , то формула дозволяє знайти оригінал для зображення , аргумент якого зміщений на .

Приклад 2. Знайти оригінал за зображенням

Розвязання

У силу формули і теореми зсуву, виділивши в знаменнику повний квадрат по р , маємо:

Відповідь:

Приклад 3. Знайти оригінал, зображення якого задається формулою

Розвязання

Відповідь:

6.5 Диференціювання зображення

Теорема: Якщо , то , тобто множення оригіналу на веде до диференціювання зображення.

Доведення

Нехай

Диференціювання останнього інтеграла за параметром р дає

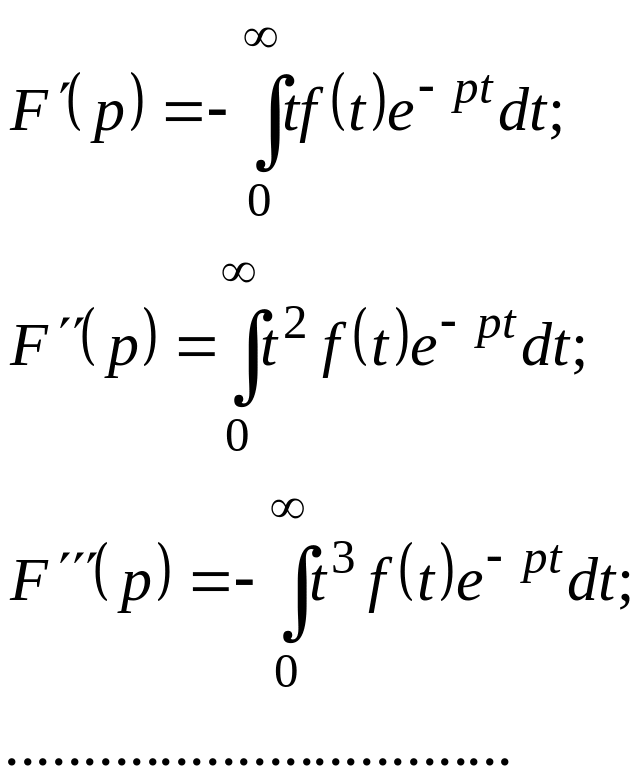
Отже:

(6.5.1)

Зокрема, поклавши в цій формулі і використовуючи знаходиться зображення степеневої функції

отже

(6.5.2)

Ураховуючи, що на підставі теореми зсуву маємо:

(6.5.3)

Приклад 1. Знайти зображення оригіналу

Розвязання

Застосовуючи формули (5.5.3) і (5.5.2), а також властивість лінійності, одержуємо:

Відповідь:

Приклад 2. Знайти зображення оригіналу

Розвязання

Відомо, що .

Отже,

Відповідь: