Методические рекомендации к решению задач заданных с помощью графовых моделей (198–227)
Имеется несколько способов задания графа. Во многих случаях граф удобно задавать в виде матрицы смежности вершин, матрицы смежности дуг или матрицы инцидентности.
Матрицей
смежности вершин
орграфа называется квадратная матрица
А,
каждый ij-ый
элемент которой численно равен количеству
дуг, идущих из вершины Еi
в вершину
Еj.
Если G=(E,
)
– неориентированный граф, то ему
соответствует симметричная матрица
смежности, так как дуги (Еi,
Еj)
и (Еj
,Еi)
существуют одновременно. Если G=(E,
)
– орграф, то соответствующая ему матрица
смежности может не являться симметричной.
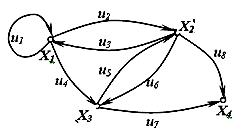
Рисунок 3 – Изображение ориентированного графа
Матрица смежности вершин графа (рисунка 3) представлена в таблице 13.
Таблица 13 – Матрица смежности вершин графа
Еj Еi |
Е1 |
Е2 |
Е3 |
Е4 |
Е1 |
1 |
1 |
1 |
0 |
Е2 |
1 |
0 |
1 |
1 |
Е3 |
0 |
1 |
0 |
1 |
Е4 |
0 |
0 |
0 |
0 |
Матрицей
смежности дуг (ребер)
орграфа (графа) называется квадратная
матрица А,
каждый ij-ый
элемент которой равен единице, если
конечная вершина дуги
является начальной вершиной дуги
(если ребра имеют общую вершину), и нулю
во всех остальных случаях. В таблице 14
приведены матрица смежности ребер и
(дуг) графа, изображенного на рисунке
3.
Таблица 14 – Матрица смежности ребер
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Матрицей инцидентности орграфа называется прямоугольная матрица А, строки которой соответствуют вершинам, столбцы – дугам, а элементы равны 1, -1 или 0. При этом на пересечении вершины Е и дуги ставится значение ε (E, ) = 1, если Е – начальная вершина дуги , ε (E, ) = -1, если Е – конечная вершина дуги, и ε (E, ) = 0, если Е не инцидентна .
Если G – неориентированный граф, то можно использовать значения ε = 0, ε = 1.