Вопросы и упражнения

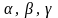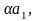
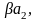
1. Доказать, что если a₁ + a₂ + a₃ = 0, то для любых векторы 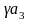линейно зависимы.

2. Векторы a₁, a₂ являются линейно зависимыми. Доказать, что векторы b₁ = 2a₁ + a₂, b₂ = a₁ + 2a₂ также линейно зависимы.

3. Векторы a₁, a₂ являются линейно независимыми. Доказать, что векторы b₁ = 2a₁ – a₂, b₂ = a₁ – 2a₂ также линейно независимы.

4. Доказать, что для любых трех векторов a₁, a₂, a₃ и любых трех чисел векторы линейно зависимы.

5. Векторы a₁, a₂, a₃ являются линейно независимыми. Доказать, что векторы b₁ = a₁ + a₂ + a₃, b₂ = – a₁ + a₃, b₃ = a₂ + a₃ также линейно независимы.

3.4. Геометрический смысл линейной зависимости и независимости векторов на плоскости и в трехмерном пространстве

Теорема 3.4.1. Два геометрических вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Доказательство. Необходимость. Пусть векторы и линейно зависимы, следовательно, 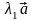+ = , причем хотя бы одно из чисел ₁, ₂ отлично от 0. Допустим для определенности ₂  0. Тогда

 +   =  ,  =  ,

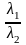т. е. векторы и коллинеарны.

Достаточность. Пусть векторы и коллинеарны. Будем считать, что среди них нет нулевого вектора, ибо в противном случае в силу теоремы 3.3.2 эти векторы будут линейно зависимы.

Если ненулевые векторы и коллинеарны, то в соответствии с теоремой 3.1.2 вектор представим в виде =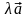 . Тогда  + (–1)  =  , что и означает линейную зависимость векторов и .

Следствие 3.4.1. Любые два неколлинеарных вектора и являются линейно независимыми.

Теорема 3.4.2. Три вектора в линейном пространстве V ³ являются линейно зависимыми тогда и только тогда, когда они компланарны.

Доказательство. Необходимость. Пусть векторы ,  ,  линейно зависимы, следовательно, существуют такие вещественные числа , , , что + + 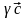= , при этом хотя бы одно из них не равно нулю. Допустим для определенности, что   0. Тогда

+ + =

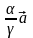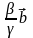или

= .

Векторы , коллинеарны соответственно векторам и , а их сумма, т. е. вектор , будет лежать в плоскости векторов и . Следовательно, векторы , , компланарны.

Достаточность. Пусть векторы , , компланарны. Будем считать, что среди них нет ни одной пары коллинеарных, ибо в противном случае в силу теоремы 3.3.3 три данных вектора будут линейно зависимыми.

П

Рис. 3.4.1

риведем векторы ,  ,  к общему началу О (рис. 3.4.1). Проведем через точку С прямую С , параллельную вектору и пересекающую прямую О в точке В. Далее параллельно вектору спроектируем точку С на прямую О . Векторы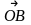 и , а также 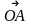и коллинеарны. Тогда в силу теоремы 3.1.2 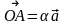, = . Однако = + = + , откуда + + (–1)  =  , что и означает линейную зависимость векторов ,  ,  .

Следствие 3.4.2. Если векторы , , некомпланарны, то они линейно независимы в V ³.

Следствие 3.4.3. Каковы бы ни были два неколлинеарных вектора , на плоскости, всякий третий вектор , лежащий в этой же плоскости, может быть разложен по векторам и в виде = + .

Теорема 3.4.3. Любые четыре вектора линейного пространства V ³ линейно зависимы.

Доказательство. Пусть ,  ,  ,  — произвольные векторы в пространстве V ³. Будем считать, что среди этих векторов никакие три не являются компланарными, ибо в противном случае данные четыре вектора будут заведомо линейно зависимы.

П

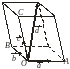
Рис. 3.4.2

риведем все векторы к общему началу О (рис. 3.4.2). Проведем через конец вектора плоскости параллельные плоскостям, в которых лежат пары векторов и , и , и соответственно. Обозначим через A, B, C соответственно точки пересечения указанных плоскостей с прямыми О , О , О .

Векторы и , и , 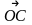и коллинеарны. Поэтому по теореме 3.1.2 = , = , = . Однако = + + , откуда + + +(–1) = , что и означает линейную зависимость векторов , , , .

Следствие 3.4.4. Каковы бы ни были три некомпланарных вектора линейного пространства V ³, любой четвертый вектор из этого пространства может быть разложен по этим векторам.