
- •Глава 3. Линейные пространства Глава 3. Линейные пространства
- •3.1. Линейные операции над векторами
- •Вопросы и упражнения
- •3.2. Линеал
- •Вопросы и упражнения
- •3.3. Линейная зависимость и независимость векторов
- •Вопросы и упражнения
- •3.4. Геометрический смысл линейной зависимости и независимости векторов на плоскости и в трехмерном пространстве
- •Вопросы и упражнения
Вопросы и упражнения
1. Какие векторы называются сонаправленными?
2. Какие векторы называются равными?
3. Являются ли два произвольных вектора компланарными?
Ответ: 1) нет, никогда; 2) да, всегда; 3) да, если они коллинеарны; 4) нет, если они неколлинеарны.
4. Могут ли быть равными два неколлинеарных вектора?
Ответ: 1) нет; 2) да; 3) да, если они имеют одинаковую длину; 4) да, если они ненулевые.
5. Если орты двух векторов противоположны, то каким свойством будут обладать указанные векторы?
Ответ: 1) коллинеарны и сонаправлены; 2) коллинеарны и противоположно направлены; 3) один из векторов нулевой; 4) оба вектора нулевые.
7. Что называется разностью двух векторов?
8. Как определяется произведение геометрического вектора на вещественное число?
9. Проверить
на чертеже справедливость тождества
 .
.
10. Вектор делит угол между неколлинеарными векторами и пополам. Каким свойством обладают эти векторы?
Ответ:
1)
 ;
2)
;
2)
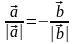 ;
3)
;
3)
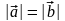 ;
4)
;
4)
 .
.
11.
В треугольнике ABC
 .
Выразить медианы
.
Выразить медианы
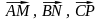 через векторы
через векторы
 и
.
и
.
Ответ:
 .
.
3.2. Линеал
Определение 3.2.1. Линейным пространством (линеалом) называют множество L элементов произвольной природы, называемых векторами, для которого:
задано правило, по которому любым двум элементам x L, y L сопоставляется элемент s L, называемый их суммой и обозначаемый s = x + y;
задано правило, по которому каждому элементу x L и любому вещественному числу R сопоставляется элемент p L, называемый произведением x на и обозначаемый p = x;
заданные правила при любых x, y, z L и любых вещественных числах , R подчинены аксиомам:
1 x + y = y + x;
2 (x + y) + z = x + (y + z);
3 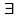 0 L,
что
x + 0 = x;
0 L,
что
x + 0 = x;
4 для x L y L , что x + y = 0;
5 (x) = ()x;
6 ( + )x = x + x;
7 (x + y) = x + y;
8 1·x = x.
Следует отметить, что в приведенном определении не накладывается никаких ограничений на природу элементов множества L и конкретное задание правил операций суммы (x, y) x + y и умножения на число (, x) x.
Для задания конкретного линеала надо определить множество L и задать на нем операции сложения элементов и умножения элемента на число.
Если в качестве векторов рассматривать направленные отрезки и традиционные линейные операции, то линеалом V 1 является множество всех свободных векторов на прямой. Линеал V 2 — множество всех свободных векторов на плоскости. Линеал V 3 — множество всех свободных векторов в трехмерном пространстве.
Линеал = {0}, состоящий только из нулевого элемента 0, является простейшим.
Другим
примером является линеал
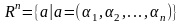 —
множество упорядоченных наборов n
вещественных
чисел, где n
— произвольное число, причем линейные
операции вводятся так:
—
множество упорядоченных наборов n
вещественных
чисел, где n
— произвольное число, причем линейные
операции вводятся так:
a + b = (α1, α2, …, αn) + (β1, β2, …, βn) = (α1 + β1, α2 + β2, …, αn + βn),
(α1, α2, …, αn) = (α1, α2, …, αn).
Линеал иногда называют координатным пространством.
Множество всевозможных матриц фиксированного размера с введенными на этом множестве операциями является линейным пространством.
Отметим, что все линеалы, за исключением простейшего линеала , имеют бесконечное количество элементов. Поскольку элементами линеалов являются векторы, то линейные пространства называют векторными пространствами.
В
дальнейшем, во избежание недоразумений,
где это необходимо, векторы пространств
V 1,
V 2,
V 3
будем называть геометрическими
векторами
и выделять стрелкой
 и т. д.
и т. д.
