Вопросы и упражнения

1. Может ли конечное множество ненулевых векторов образовывать линейное пространство?

Ответ: 1) да; 2) нет; 3) да, если они неколлинеарны; 4) да, если они некомпланарны.

2. Является ли множество всевозможных компланарных единичных векторов линейным пространством?

Ответ: 1) да, всегда; 2) нет, никогда; 3) да, если к этому множеству добавить нулевой вектор; 4) нет, так как в этом множестве не определена сумма двух элементов и произведение элемента на число.

3. Образует ли множество полиномов степени не выше заданной линейное пространство?

Ответ: 1) да, если к этому множеству добавить 0; 2) нет, никогда; 3) да, всегда; 4) нет, поскольку полиномы не являются взаимно простыми.

3.3. Линейная зависимость и независимость векторов

Пусть L — произвольное линейное пространство, a_i  L, 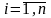 — его элементы (векторы).

Определение 3.3.1. Выражени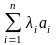е , где , — произвольные вещественные числа, называется линейной комбинацией векторов a₁, a₂,…, a_n.

Если вектор р =  , то говорят, что р разложен по векторам a₁, a₂,…, a_n.

Определение 3.3.2. Линейная комбинация векторов называется нетривиальной, если среди чисел есть хотя бы одно отличное от нуля. В противном случае, линейная комбинация называется тривиальной.

Определение 3.3.3. Векторы a₁, a₂,…, a_n называются линейно зависимыми_, если существуют их нетривиальная линейная комбинация, такая что

 = 0.

Определение 3.3.4. Векторы a₁, a₂,…, a_n называются линейно независимыми_, если равенство  = 0 возможно лишь в случае, когда все числа ₁, ₂,…, _n одновременно равны нулю.

Отметим, что всякий ненулевой элемент a₁ можно рассматривать как линейно независимую систему, ибо равенство a₁ = 0 возможно лишь при условии  = 0.

Теорема 3.3.1. Необходимым и достаточным условием линейной зависимости a₁, a₂,…, a_n является возможность разложения, по крайней мере, одного из этих элементов по остальным.

Доказательство. Необходимость. Пусть элементы a₁, a₂,…, a_n линейно зависимы. Это означает, что  = 0, причем хотя бы одно из чисел ₁, ₂,…, _n отлично от нуля. Пусть для определенности ₁  0. Тогда

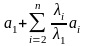 = 0 ,

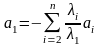т. е. элемент a₁ разложен по элементам a₂, a₃, …, a_n.

Достаточность. Пусть элемент a₁ разложен по элементам a₂, a₃, …, a_n, т. е. a₁ = 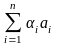 . Тогда 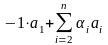 = 0, следовательно, существует нетривиальная линейная комбинация векторов a₁, a₂,…, a_n, равная 0, поэтому они являются линейно зависимыми.

Теорема 3.3.2. Если хотя бы один из элементов a₁, a₂,…, a_n нулевой, то эти векторы линейно зависимы.

Доказательство. Пусть a_n = 0, тогда 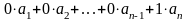= 0, что и означает линейную зависимость указанных элементов.

Теорема 3.3.3. Если среди n векторов какие-либо p (p < n) векторов линейно зависимы, то и все n элементов линейно зависимы.

Доказательство. Пусть для определенности элементы a₁, a₂,…, a_p линейно зависимы. Это означает, что существует такая нетривиальная линейная комбинация, что 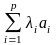 = 0. Указанное равенство сохранится, если добавить к обеим его частям элемент 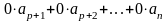. Тогда +  = 0, при этом хотя бы одно из чисел ₁, ₂,…, _p отлично от нуля. Следовательно, векторы a₁, a₂,…, a_n являются линейно зависимыми.

Следствие 3.3.1. Если n элементов линейно независимы, то любые k из них линейно независимы (k < n).

Теорема 3.3.4. Если векторы a₁, a₂,…, a_n-1 линейно независимы, а элементы a₁, a₂,…, a_n-1, a_n линейно зависимы, то вектор a_n можно разложить по векторам a₁, a₂,…, a_n-1.

Доказательство. Так как по условию a₁, a₂,…, a_n-1, a_n линейно зависимы, то существует их нетривиальная линейная комбинация  = 0, причем 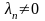(в противном случае, окажутся линейно зависимыми векторы a₁, a₂,…, a_n-1). Но тогда вектор

,

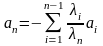что и требовалось доказать.