Глава 2. Введение в математический анализ.
1. Функции одной независимой переменной.
Функцией называется закон, или правило, согласно которому каждому действительному числу х из некоторого множества Х действительных чисел ставится в соответствие единственное, вполне определенное число у. Это соответствие между числами обозначается так: y=f(x). При этом множество Х называется областью определения функции, а множество чисел вида y=f(x), где пробегает все множество Х, - ее множеством значений. Область определения функции обозначается через D(f), а множество значений - через Е(f).
Основными элементарными функциями называются сле-дующие функции:
1. Степенная функция у=х.
2. Показательная функция у=аõ, ãäå à0 è à1.
3. Логарифмическая функция у=logax, ãäå à0 è à1.
4. Тригонометрические функции у=sin(x), y=cos(x),
y=tg(x), y=ctg(x), y=sec(x), y=cosec(x)/
5. Обратные тригонометрические функции
y=arcsin(x), y=arccos(x), y=arctg(x), y=arcctg(x).
Элементарными функциями называются функции, которые получаются из основных с помощью четырех арифметических действий и операции образования сложной функции (функции от функции).
Примером элементарной функции может служить абсо-лютная величина (модуль) числа х:
Геометрически х есть расстояние на числовой прямой от точки с координатой х до начала отсчета. В общем случае х-а есть расстояние между точками с координатами х и а.
Графиком функции y=f(x) называется множество точек плоскости ХОУ с координатами (х,f(x)), где хD(f).
Функция y=f(x), область определения которой симметрична относительно нуля, называется четной (соответственно нечет-ной), если для любого хD(f) выполняется равенство f(-x)=f(x) (соответственно f(-x)=-f(x)). График четной функции симметричен относительно оси ОУ, а нечетной - относительно начала системы координат.
Положительное число Т называется периодом функции y=f(x), если для всех х,(х+Т)D(f) выполняется равенство f(x+T)=f(x). Если функция имеет какой-нибудь период, то она называется периодической, а наименьший ее период - ее основным периодом.
Пример 1. Найти область определения функции
Решение. В первом слагаемом подкоренное выражение должно быть неотрицательным, а во втором аргумент арк-синуса по абсолютной величине не должен превосходить единицы. Поэтому область определения функции опреде-ляется системой неравенств
Решением этой системы неравенств, а с ним и областью определения функции, является интервал [-1/3,1/2].
Пример 2. Установить четность или нечетность
функции
Решение. Прежде всего заметим, что функция определена лишь при тех значениях х, для которых
(õ+3)/(x-3)>0.
Это неравенство эквивалентно следующему:х>3, откуда область определения функции D(f)=(-,-3)(3,) сим-метрична относительно нуля. Для любого хD(f) имеем:
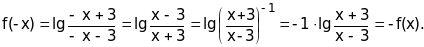
Следовательно, данная функция является нечетной.
Пример 3. Найти основной период функции
f(x)=sin6x+tg4x.
Решение. Основным периодом синуса является число 2, а тангенса - . Значит, основной период для первого слагаемого равен 2/6=/3, а для второго - /4. Ясно, что наименьшим периодом нашей функции будет наименьшее общее кратное чисел /3 и /4, то есть .
Задача 9. Найти область определения функций.
N |
Функции |
1 |
y=ln(sin2x); y= |
2 |
y=sin(ln2x); y= |
3 |
y= |
4 |
y= |
5 |
y= |
6 |
y= |
7 |
y= |
8 |
y= |
9 |
y= |
10 |
y= |
;
y=
;
;
y=
;
;
y=EMBED Equation
;
y=arcsin(lnx);
;
y=
;
y=
;
;
y=
;
y=
;
;
y=
;
y=
;
;
y=
;
y=
;
;
y=
;
y=
;
;
y=
;
y=
;
;
y=
;
y=
;