2.4. Условный экстремум функции двух переменных

Сведения из теории

Ранее мы исследовали на экстремум функцию двух переменных, не накладывая никаких условий на переменные и . Сейчас мы рассмотрим случай, когда и связаны друг с другом функциональной зависимостью. Она задается уравнением (называется уравнением связи). Мы рассмотрим простой вариант, когда из уравнения связи выражается явно как функция , т.е. .

Метод решения состоит в следующем. В функцию вместо символа подставим формулу , полученную из уравнения связи: . Очевидно, что при этом функция двух переменных превратится в функцию одной переменной .

Пример. Исследовать функцию на экстремум, если и связаны уравнением .

Решение. Из уравнения связи выразим : . Тогда . Вычислим . Стационарная точка . В ней квадратичная функция имеет минимум, который равен .

Ответ. .

2.5. Наибольшее и наименьшее значения функции двух переменных на замкнутой области

Сведения из теории

Пусть функция определена и непрерывна на замкнутой области .

Определение Значение функции в точке называется наибольшим (наименьшим) на замкнутой области , если в любой другой точке значение функции ( или для наименьшего ).

Свои наименьшее и наибольшее значения функция может принимать либо в стационарных точках ( точках, в которых и ) при условии, что они принадлежат области , либо на границе области . Этот факт определяет метод нахождения наибольшего и наименьшего значений функции.

1. Вычислим частные производные и приравняем их нулю, т.е. и . Найдем стационарные точки. Из них выберем только те, которые принадлежат области , остальные просто отбросим.

2. В отобранных стационарных точках вычислим значения функции.

Замечание Обратите внимание, не нужно исследовать каждую отобранную стационарную точку на наличие в ней экстремума и его типа. В данной задаче важно только числовое значение функции в стационарной точке.

3. Исследуем поведение функции на границе области . Найдем на ней стационарные точки и в них вычислим значения функции.

4. Из всех вычисленных значений функции выберем максимальное и минимальное. Максимальное значение является наибольшим значением функции, а минимальное значение является наименьшим значением функции на замкнутой области .

П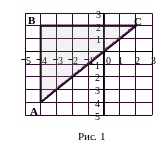 ример. Найти наибольшее и наименьшее значения функции в замкнутой области , ограниченной графиками функций: , , .

Решение. Прежде всего следует нарисовать область (Рис.1 ).

1. Найдем стационарные точки.

   стационарная точка.

Так как точка , то в ней нужно вычислить значение функции. =

2. Найдем стационарные точки на отрезке границы АВ.

На отрезке границы АВ функция 2-х переменных становится функцией одной переменной , а именно: . Исследование на границе является задачей нахождения наибольшего и наименьшего значений функции одной переменной на отрезке. Поэтому вычислим  . Следовательно, точку просто отбрасываем.

Вычислим значения функции на концах отрезка АВ:

= ; =

3. Найдем стационарные точки на отрезке границы ВС.

На отрезке границы ВС функция 2-х переменных становится функцией одной переменной , а именно: .

Вычислим . Следовательно, точка , а значит нужно вычислить в ней значение функции :

= .

Вычислим значения функции на концах отрезка ВС:

(вычислено в п. 2) , = .

4. Найдем стационарные точки на отрезке границы АС. .

На отрезке границы АС функция 2-х переменных становится функцией одной переменной , а именно:

.

Вычислим . Следовательно, точка , а значит в ней нужно вычислить значение функции : .

Значения функции на концах отрезка АС вычислены в предыдущих пунктах.

5.

Ответ. , .