2.2. Полный дифференциал функции двух и трех переменных.

Линеаризация функции двух и трех переменных. Использование полного дифференциала в приближенных вычислениях.

Сведения из теории

Из теории функций двух переменных известно, что, если функция имеет в точке непрерывные частные производные и , то ее приращение , порожденное приращениями переменных и , представимо в виде .

Символ означает, что, если и стремятся к нулю, то слагаемое стремится к нулю еще быстрее. Если это слагаемое отбросить, то получится приближенное равенство

.

Выражение, которое осталось справа, называется полным дифференциалом функции двух переменных . Обозначение . Если символы и заменить символами и , называемые дифференциалами и , то полный дифференциал примет вид .

Из определения полного дифференциала следует, что для любой фиксированной точки разница между точным приращением функции , порожденным приращениями и , и дифференциалом , вычисленным в точке , есть величина бесконечно малая, т.е. . Отсюда следует цепочка приближенных равенств :



Если обозначить , , соответственно , , то приближенная формула примет вид

.

Поясним смысл этой формулы: исходная функция с произвольной формулой в окрестности точки заменяется на линейную функцию двух переменных вида . Главное достоинство последней функции  простота вычисления. Для этой замены есть название  линеаризация функции.

Геометрически линеаризация функции двух переменных означает замену ординаты поверхности, являющейся графиком функции , на ординату касательной плоскости, проведенной к графику функции, в точке .

Для функции трех переменных полный дифференциал имеет вид . Линеаризация функции трех переменных в окрестности точки задается следующим приближенным равенством

.

Рассмотрим на примере, как линеаризация функции используется для приближенного вычисления значений функции при «неудобных» значениях переменных.

Пример. Вычислить приближённо с помощью полного дифференциала значение выражения .

Решение. Прежде всего, нужно ввести функцию, частным значением которой является искомое выражение. В данном примере это будет функция трех переменных . Искомое выражение является ее значением при . Далее нужно подобрать значения , , такие, чтобы они, во-первых, были близки к , , и, во-вторых, значение функции вычислялось легко. Таковыми являются , , . Легко вычислить . Линеаризацию функции нужно проводить в окрестности точки . Для этого вычислим значения частных производных в точке .

;

;

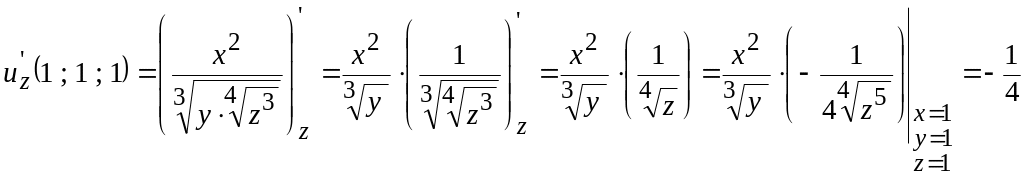
Формула линеаризации функции имеет вид:

.

Тогда .

Ответ. .

2.3. Экстремумы функции двух переменных

Сведения из теории

Напомним, что экстремумы бывают двух типов максимумы и минимумы. Экстремумы характеризуют функцию локально, только в окрестности некоторой точки. Это вытекает из самого определения экстремума.

Определение. Говорят, что функция двух переменных имеет максимум ( минимум ) в точке , если существует окрестность этой точки, для всех точек которой выполняется неравенство (соответственно для минимума ).

Доказано, что функция может принимать максимум или минимум только в тех точках, в которых и или эти частные производные не существуют. Известно также, что условие еще не гарантирует наличие экстремума в точке . Для этого еще должны выполняться так называемые достаточные условия экстремума. Они формулируются в виде теоремы.

Теорема (достаточные условия экстремума)

Пусть в точке частные производные или эти частные производные не существуют. Вычислим для этой точки три числа: . По ним вычислим выражение . Тогда:

1. если , то экстремум есть, при этом, если число , то минимум, а если , то максимум;

2. если , то экстремума нет;

3. если , для исследования функции на экстремум нужны дополнительные исследования с использованием частных производных более высокого порядка.

Пример. Исследовать на экстремумы функцию .

Решение.

Прежде всего, найдем точки, в которых частные производные и равны нулю: . Система имеет два решения и .

Далее найдем формулы частных производных 2-го порядка.

.

Сначала исследуем достаточные условия для точки .

.

Вычислим , следовательно, в точке экстремума нет.

Теперь исследуем достаточные условия для точки .

.

Вычислим , следовательно, в точке экстремум есть. Так как , то минимум. Вычислим его

.

Ответ. .