Наступление события, благоприятствующие исходы

Каждое случайное событие определяется как подмножество в множестве элементарных событий . При этом те элементарные события из , при которых событие наступает (т.е. принадлежит подмножеству ) называют благоприятствующими событию . Говорят, что событие произошло (наступило, осуществилось, реализовалось), если результатом эксперимента явился элементарный исход , принадлежащий ( ).

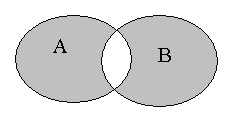
Совместные (совместимые), несовместные (несовместимые) события

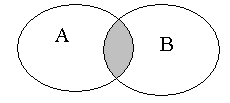
Два события называются совместными (совместимыми) в данном опыте, если появление одного из них не исключает появления другого.

Два события называются несовместными (несовместимыми) в данном опыте, если они не могут произойти вместе при одном и том же испытании. Несколько событий называются несовместными, если они попарно несовместны.

Другими словами, события и совместны, если соответствующие множества и имеют общие элементы, и несовместны в противном случае, если появление одного из них исключает появление другого, и соответствующие множества и не имеют общих элементов, т.е. пересечение этих множеств является пустым множеством.

Достоверное и невозможное события

Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий .

Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий .

Событие, совпадающее с пустым множеством , называется невозможным событием, а событие, совпадающее со всем множеством , называется достоверным событием.

События называют равновозможными, если нет основания полагать, что одно событие является более возможным, чем другие.

Теория вероятностей есть наука, изучающая закономерности случайных событий. Одной из главных задач в теории вероятностей является задача определения количественной меры возможности появления события.

Алгебра событий Операции над событиями (сумма, разность, произведение)

С каждым испытанием связан ряд интересующих нас событий, которые, вообще говоря, могут появляться одновременно. Например, при бросании игральной кости (т.е. кубика, на гранях которого имеются очки 1, 2, 3, 4, 5, 6) событие есть выпадение двойки, а событие – выпадение четного числа очков. Очевидно, что эти события не исключают друг друга.

Пусть все возможные результаты испытания осуществляются в ряде единственно возможных частных случаев, взаимно исключающих друг друга. Тогда:

• каждый исход испытания представляется одним и только одним элементарным событием;

• всякое событие , связанное с этим испытанием, есть множество конечного или бесконечного числа элементарных событий;

• событие происходит тогда и только тогда, когда реализуется одно из элементарных событий, входящих в это множество.

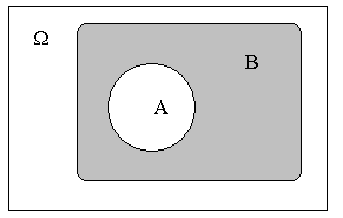
Другими словами, задано произвольное, но фиксированное пространство элементарных событий , которое можно представить в виде некоторой области на плоскости. При этом элементарные события – это точки плоскости, лежащие внутри . Поскольку событие отождествляется с множеством, то над событиями можно совершать все операции, выполнимые над множествами. То есть, по аналогии с теорией множеств, строится алгебра событий. В частности, определены следующие операции и отношения между событиями:

(отношение включения множеств: множество является подмножеством множества ) – событие A влечет за собой событие В. Иначе говоря, событие В происходит всякий раз, как происходит событие A. (отношение эквивалентности множеств) – событие тождественно или эквивалентно событию . Это возможно в том и только в том случае, когда и одновременно , т.е. каждое из них происходит всякий раз, когда происходит другое. ( ) – сумма событий. Это событие, состоящее в том, что произошло хотя бы одно из двух событий или (не исключающее логическое «или»). В общем случае, под суммой нескольких событий понимается событие, состоящее в появлении хотя бы одного из этих событий.

( ) – произведение событий. Это событие, состоящее в совместном осуществлении событий и (логическое «и»). В общем случае, под произведением нескольких событий понимается событие, состоящее в одновременном осуществлении всех этих событий. Таким образом, события и несовместны, если произведение их есть событие невозможное, т.е. .

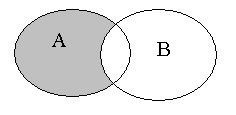
(множество элементов, принадлежащих , но не принадлежащих ) – разность событий. Это событие, состоящее из исходов, входящих в , но не входящих в . Оно заключается в том, что происходит событие , но при этом не происходит событие .

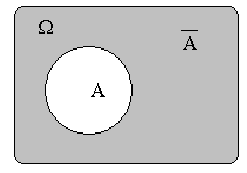
Противоположным (дополнительным) для события (обозначается ) называется событие, состоящее из всех исходов, которые не входят в . Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Событие , противоположное событию , происходит тогда и только тогда, когда событие не происходит. Другими словами, наступление события означает просто то, что событие не наступило.

Симметрическая разность двух событий и (обозначается ) называется событие, состоящее из исходов, входящих в или , но не входящих в и в одновременно. Смысл события состоит в том, что наступает одно и только одно из событий или . . Обозначается симметрическая разность: или .