Тригонометрическое представление

Посмотрите на рисунок 9. Комплексное число однозначно определяется своим модулем (расстоянием до точки ) и углом между и действительной осью — этот угол называется аргументом комплексного числа и обозначается так:

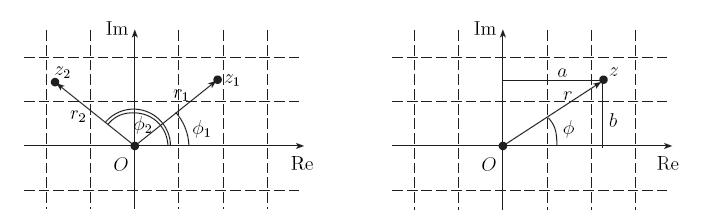
Рис.9 Комплексное число однозначно определяется своим модулем и аргументом .

Определение 6

Комплексное число с модулем и аргументом

мы будем обозначать как

Задача 57[9]

Докажите, что действительная и мнимая части числа равны

и

Задача 58[9]

Запишите в виде следующие комплексные числа:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

Задача 59[9]

Запишите в виде ( , ) следующие комплексные числа:

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

Теорема 2

При умножении двух комплексных чисел их модули умножаются а аргументы складываются:

Доказательство теоремы отложим на потом. Посмотрите на рисунок 10, где пояснено содержание теоремы.

Рис. 10. При умножении чисел их модули умножаютcя, a аргументы складываются: ,

Приведем несколько примеров того, как работает эта теорема:

Пример 1.

Пример 2.

Величину вычислим двумя способами:

и в то же время

Как видите, оба метода приводят к одному и тому же результату.

Пример 3.

Величину вычислим двумя способами:

и в то же время

в итоге снова получаем .

Доказательство теоремы 2.

Для доказательства теоремы достаточно показать, что

Это действительно так. Раскрывая левую часть, получим:

В скобках стоят формулы для косинуса суммы и синуса суммы.

Примечание Интересна следующая интерпретация комплексных чисел: каждое комплексное число — это преобразование комплексной плоскости, а именно, гомотетия относительно центра с коэффициентом и поворот против часовой стрелки на угол . Тогда умножение комплексных чисел соответствует композиции соответствующих преобразований.

Задача 60[10]

Найдите чему равно .

Решение

Задача 61[10]

Рассмотрите два уравнения:

Выразите из них и

Задача 62[10]

Найдите значение .

Покажите, что это действительное число, большее .

Задача 63[10]

Найдите

а) такое, что  ; б) ;

в) ;

Решение

а) ;

б) ;

в) .

Извлечение корней

Возвести число в -ую степень значит возвести в -ую степень модуль, а аргумент умножить на :

Это правило следует непосредственно из теоремы 2 предыдущего параграфа.

Задача обратная возведению в -ую степень — это извлечение корней -ой степени.

Задача 64[9]

Дано уравнение относительно :

[3]

где  — некоторое комплексное число. Найдите все комплексные числа , удовлетворяющие этому уравнению.

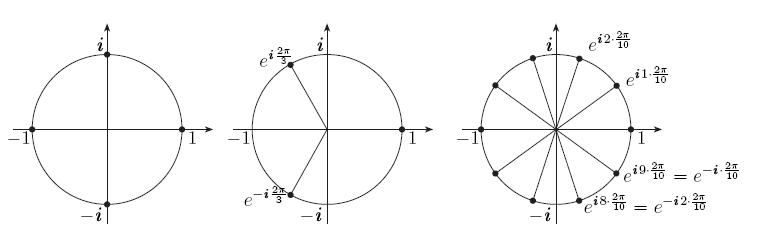
Рис. 11. Корни уравнений: а) , б) , в)

Прежде, чем решать это общее уравнение, рассмотрим частный случай , :

Один из корней равен , второй равен . Есть ли другие корни? Так как , то корни этого уравнения имеют единичный модуль и лежат на единичной окружности. Комплексные числа, лежащие на единичной окружности, имеют вид:

После возведения в степень имеем:

Осталось найти такие , что

Последнее равенство верно, когда аргумент кратен полному углу :

Получили, что все комплексные числа вида

являются корнями уравнения . Корень совпадает с корнем .

Для эти числа отмечены на рисунке 11(в).